Расчёт дисперсии, плотности вероятности и функции распределения гармонического сигнала, страница 2

,

где ‑функция распределения.

‑независим от времени так как процесс эргодический.

.

, .

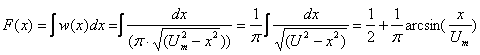График функции распределения (для ) приведен на рис. 3.

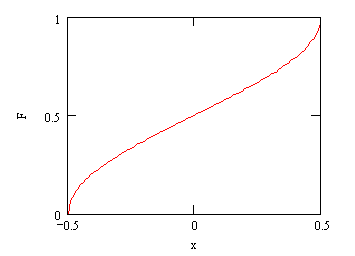
Рис. 3 График функции распределения (для ).

График функции распределения (для ) приведен на рис. 4.

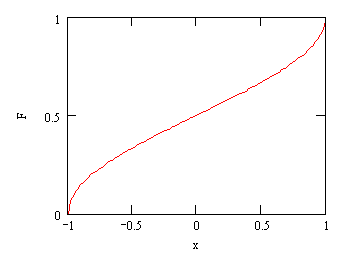
Рис. 4 График функции распределения (для ).

Рассчитаем дисперсию:

.

Определим m(t):

,

где ,

,.

.

.

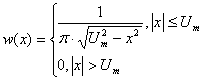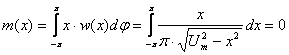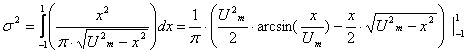2.        Рассчитать значения ,  и построить графики нормального случайного процесса с нулевым средним и дисперсией, соответствующей варианту задания. Провести моделирование.

.

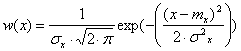т.к. , уравнение принимает следующий вид:

,.

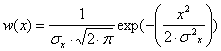График плотности вероятности (для , ) нормального случайного процесса приведен на рис. 5.