Воспитание алгоритмического мышления на уроках математики, страница 2

Затем предлагаем детям придумать другой алгоритм построения такого же квадрата. Приходим к выводу, что различные алгорит­мы могут давать одинаковый результат. Луч­шим из них считается тот, который позво­ляет  просто и быстро  получить результат.

Следующий шаг в работе с алгоритмами связан со знакомством с понятием цикла. Он начинается при изучении темы «Числа от 1 до 10. Число 0». Знакомство с циклами осуществляется с помощью простых заданий по вычерчиванию отрезков заданной длины. В качестве первого упражнения рассмотрим такое: что начертит робот, выполнив команды:

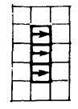
Затем спрашиваем детей: различны ли команды в программе? Сколько раз повто­ряется команда «Вправо»? В заключение зна­комим с  новой  формой  записи  алгоритма:

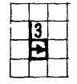
Такая   работа   может   быть   продолжена, но уже на более высоком уровне при вычерчивании геометрических узоров с заданными закономерностями: «Продолжите узор в оставшихся клетках; продолжите такой же узор, исполнив команды, сравните получен­ные результаты, запишите алгоритм построе­ния узора».

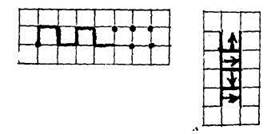
Проведение такой работы с I класса позво­лит закрепить навыки построения отрезков и счета в пределах 10, явится пропедев­тикой измерения величин и познакомит с ув­лекательным миром алгоритмов. Эти упраж­нения также помогут закрепить простран­ственные представления (вверх, вниз, вправо, влево).

В процессе игры должна постоянно про­водиться работа по нахождению и устра­нению ошибок в алгоритмах. Следует знать наиболее типичные ошибки, допускаемые детьми при составлении и исполнении ал­горитмов:

1)  пропуск команд;

2)  незавершенность команд (дана коман­да «Вперед» и не указано, сколько раз нужно ее повторить);

3)  выбор ошибочной последовательности (вместо   команды   «Вправо»   дают   команду «Влево», что связано с тем, что на раннем этапе обучения дети путают понятия влево и вправо);

4)  отсутствие проверки завершенности за­дания (эти ошибки возникают при рассмот­рении циклических алгоритмов).

Исходя из перечисленных выше ошибок и следует давать соответствующие упражнения на предотвращение их. Так, в случае про­пуска команд следует предлагать строить по их алгоритму чертеж и сравнивать его с об­разцом.

Если добавить к уже известным командам новые ã, ä, å, æ то можно значительно расширить набор рисунков, которые могут построить дети. Эти команды позволят про­вести познавательные игры «Письма» и «Шахматы».

Игра «Письма» начинается с рассказа о том, для чего нужен индекс на письме и по­чему важно писать его правильно. Затем показываем, как записывают цифры индекса. Потом предлагается научить нашего робота писать эти цифры. Работа начинается с вы­полнения задания по вычерчиванию двух-трех цифр индекса по алгоритму.

Исполните команды:

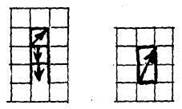
и посмотрите, что за цифра получилась. Мож­но ли по-другому записать алгоритм построе­ния этой цифры?

В заключение переходим к вычерчиванию цифры индекса по образцу и записи алго­ритма построения этой цифры.

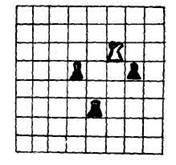
Интересна также и игра «Шахматы». Она знакомит с правилами, по которым двигаются основные шахматные фигуры, и закрепляет навыки построения алгоритмов. Рассмотрим одну из задач в этой игре: «Запишите алго­ритм, по которому ладья срубит все пешки».

Особенно полезны игры с роботом в случае, когда учащиеся имеют доступ к компьютеру. В дочисловой период достаточно использо­вание 7 клавиш, управляющих движением светящейся точки (курсор), которая переме­щается по экрану. Здесь применяются кла­виши:

ç, è, é, ê — управление  перемещением курсора;

Т —фиксация точки;

К —карандаш;

Р —резинка (стирает все).

После нажатия клавиша «Т» фиксирует светом точку, где сейчас находится курсор, и   остается   светящейся   после   его   сдвига.

Освоение клавиш по управлению переме­щением курсора в заданном направлении можно начать с игры «Футбол». Исходное положение: на экране курсор и «ворота» — полукруг, диаметр которого — линия ворот, полуокружность — «сетка». Линия ворот на­ходится в одном из основных направлений движения курсора. Задание состоит в том, чтобы нажать нужную клавишу и держать ее до тех пор, пока курсор не попадет в ворота. После «гола» игра повторяется с новым ис­ходным положением. Попытка перемещения курсора в неправильном положении блоки­руется.   В   ходе   игры   варьируются   размещение на экране курсора и ворот, направ­ление движения курсора. Игра продолжается до тех пор, пока не будет выполнено задание. В  дальнейшем  задания   можно  усложнять.

Знакомство с движением курсора в четырех направлениях может быть связано с элемен­тами географии. Для этого используется игра «Карта». Исходное положение: на экра­не курсор и карта, на которой изображены наиболее распространенные звери. Задание состоит в том, чтобы привести курсор к изоб­ражению определенного зверя. Здесь можно ознакомить детей с понятиями север, юг, за­пад, восток как синонимами слов вверх, вниз, влево, вправо.

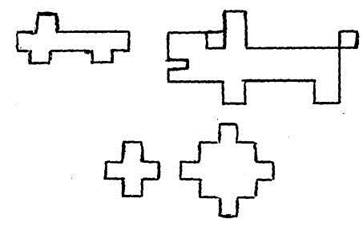
Компьютер позволит увеличить продуктив­ность работы ребенка. Более того, он позво­лит изменять масштабы реализуемых проек­тов. Теперь вместе с роботом можно строить алгоритмы вычерчивания более сложных фигур:

Дальнейшая работа с алгоритмами проис­ходит в процессе изучения основных разде­лов математики. Учащиеся вместе с учителем формируют алгоритмы измерения отрезков с помощью линейки, алгоритмы вычислений над многозначными числами  и  т. д.

Исходя из вышесказанного, мы предлагаем такую классификацию упражнений, связан­ных   с   алгоритмами   в   начальной   школе:

1)  исполнение и составление алгоритмов из окружающей жизни;

2)  изменение алгоритмов;

3)  исполнение и построение алгоритмов, приводящих к одному результату;

4)  нахождение и устранение ошибок в ал­горитме;

5)  исполнение и построение алгоритмов на геометрическом материале;

6)  исполнение и построение простейших алгоритмов с циклами;

7)  исполнение   и построение ветвящихся алгоритмов.

Следует отметить на раннем этапе обуче­ния ценность задач, предлагающих испол­нить алгоритмы, связанные с обменом содержимого некоторых множеств. Например: даны четыре ведерка различного цвета с раз­ным   количеством   шаров   в   каждом.

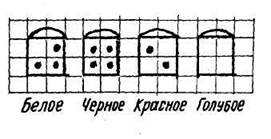Переложить шары согласно программе:  Бà Г , Кà Б, ЧàК

Вместо букв можно использовать кружки определенного цвета.

Можно познакомить детей с алгоритма­ми классификации на примере расположе­ния двух, трех чисел в порядке возраста­ния.

В начальных классах нужно использовать и ветвящиеся алгоритмы. На наш взгляд, для этого лучше всего подходят игры, предло­женные А. А. Столяром[3].

Мы показали некоторые пути знакомства с основными алгоритмами в начальной школе. Продолжить поиски новых путей по осущест­влению межпредметных связей математики и информатики в начальных классах могут учителя-практики.