Алгоритмы в обучении шестилеток математике, страница 2

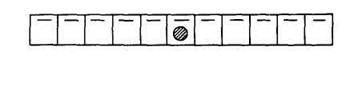
Рис. 1

В начале эксперимента описывается маши­на и рассказывается, что она может делать.

Дети знакомятся с командами. Указывается, что Коля выполняет их по шагам, смотря по тому, какая команда ему дана. Слово «команда», как правило, детям знако­мо. Коля может передвигаться влево и впра­во, вставлять или убирать кружок и останав­ливаться.

В теоретической машине Поста возможны три варианта окончания ее работы:

1) Если машина достигает команды <. стоп, то она останавливается (результативная остановка). 2) Если машина встречает невы­полнимую команду (напечатать метку в непу­стой клетке или стереть метку в пустой клетке), то она тоже останавливается (без­результатная остановка). 3) Если машина в процессе работы не доходит до результатив­ной или безрезультативной остановки, то она работает бесконечно.

В экспериментальной машине Поста тре­тий случай отсутствует. Если Коля (а его роль играет кто-нибудь из детей) обнару­жит команду !, он должен сказать, что рабо­та закончена. Если Коле нужно будет взять круг из клетки, где его нет, или вставить круг в клетку, которая заполнена, или он дошел до первой или одиннадцатой клетки и ему нужно двигаться дальше, то он должен сказать, что машина сломалась.

Играя с машиной Поста, дети знакомятся с алгоритмами (программами) и устанав­ливают их свойства: дискретность (работа по командам), детерминированность (опре­деление пути прохождения программы); ре­зультативность (получение результата или невозможность его получения — «машина сломалась»), массовость (применение прог­раммы к решению однотипных задач).

Игры с машиной Поста развивают мыш­ление детей, готовят их к восприятию ма­тематики на более высоком уровне и слу­жат хорошей пропедевтикой информатики.

Для усвоения работы машины Поста детям предлагается несколько простейших про­грамм, приводящих и к результату, и к полом­ке машины.

Экспериментатор предлагает программу, написанную на листе бумаги, и разбирает, как происходит работа по этой программе. Затем кто-нибудь из детей вызывается для выступления в роли Коли и рассказывает, как работает программа. Приведем несколько примеров вводных программ.

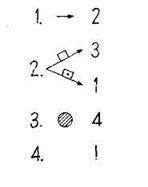
Пример 1. Предлагается программа:

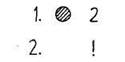
Выясняется, что, работая по этой прог­рамме, Коля должен вставить круг и закон­чить работу.

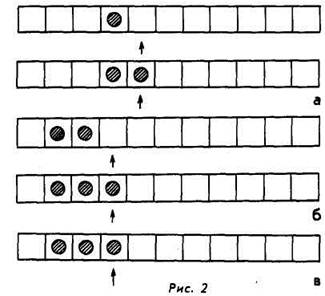
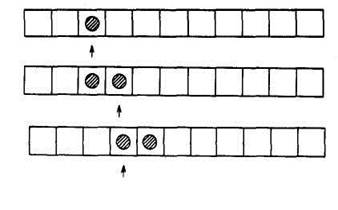
Затем дети по очереди выполняют эту программу при различном количестве кругов на ленте (рис. 2).

Положение Коли указано стрелкой. Игра проходит следующим образом.

В случае а) ребенок смотрит на команду  и  говорит: «Коля смотрит на пустую клетку. Он должен положить туда кружок»; затем, посмотрев на команду «2 !», играю­щий произносит: «Коля работу закончил» или «Работа закончена». В случае в) ре­бенок говорит, смотря на команду:  «Коле нужно вставить круг в клетку, на которую он смотрит. Клетка занята. Значит, машина сломалась».

Таким образом, в случае а) на ленте был 1 круг, а после работы машины станет 2 кру­га; в случае б) на ленте было 2 круга, а затем окажется 3; в случае в) машина «сломается», так как Коля не может вставить круг в заня­тую клетку.

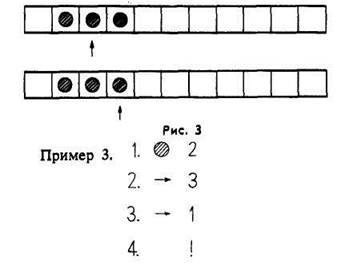
Пример 2.

1. à2  а)

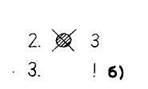В случае а) Коля уберет круг и остановит машину, оставив 2 круга на ленте; в случае б) машина сломается, так как, перейдя к нуж­ной клетке, Коля не сможет убрать из нее круг (рис. 3). Важно, чтобы дети поняли, почему машина сломалась.

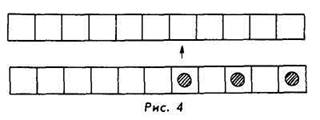
По этой программе Коля поместит в ма­шину 3 круга и дойдет до конца ленты, после чего машина сломается, так как дальше дви­гаться вправо нельзя. До команды 4 Коля не дойдет (рис. 4).

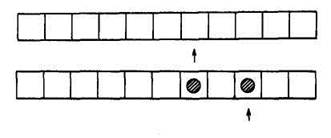
Пример 4.  

1
2
3
4

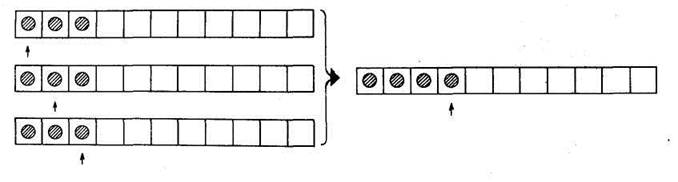
По этой программе Коля запишет на ленте только   2   круга   через   одну   клетку,   после чего машина остановится, так как Коля дой­дет до команды остановки 4 (рис. 5).

Рис. 5

Такие программы ставят своей целью обу­чить детей командам и различным типам остановки машины.

Когда дети усвоят работу машины, им предлагается игра, которая ставит своей целью прибавление единицы. Вначале рас­сматривается простая программа:

Играя с этой программой, дети обнаружи­вают, что иногда действительно приходится прибавлять единицу (рис. 6), а иногда нет (рис. 7). Все зависит от положения Коли в начале игры.

                          Рис. 6, 7

После игры с разобранной программой мы знакомим детей с программой, которая всег­да прибавляет единицу (вписывает в ленту еще 1 кружок, вне зависимости положения Коли в начале игры) при условии, что обоз­ревает заполненную клетку.

Эта программа позволяет рассмотреть прибавление единицы к числам от 1 до 10. Игры с этой программой занимают довольно много времени, так как нужно рассмотреть в каждом случае все (или почти все) поло­жения Коли.

Так, на рис. 8 разобраны все начальные положения Коли для случая 3+1=4.

После каждой игры дети пишут результаты (3+1 = 4) и проговаривают его (3 плюс 1 равняется четырем).

Аналогичная работа проводится с вычи­танием единицы. Вначале рассматривается простая программа:

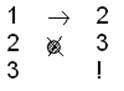Выясняется, в каком случае, играя с этой программой, можно вычесть единицу, а в ка­ком программа работать не будет.

После этого проводится игра с прог­раммой:

Эта программа всегда убирает 1 кружок с ленты при любом начальном положении Коли, обозревающего заполненную клетку. После каждой игры записывается результат (9—1=8, 8—1 = 7 и т. д.).

Приведенные примеры показывают, что любая задача приводит фактически к роду задач, возникающих в результате различных начальных положений Коли. Мы, конечно, рассмотрели не все возможные положения.

В связи с последним примером может воз­никнуть вопрос: «А не проще ли научить ребенка прибавлять или вычитать единицу другим, более простым способом (без маши­ны)?» Мы подчеркиваем, что речь идет совер­шенно не о том, чтобы учить детей прибав­лять или вычитать единицу с помощью ма­шины Поста. Конечно, дети учатся выпол­нять эти операции гораздо раньше и на более доступных объектах. Предлагая пример 4, мы ставим ребенка в такое положение, что он открывает для себя неожиданный факт: ока­зывается, и машина с послушным мальчиком Колей может прибавлять и вычитать едини­цу, если правильно отдавать команды. Имен­но с этого примера мы и начинаем детей готовить к пониманию того, что в жизни многие действия сводятся к выполнению алгоритмов. Кроме того, как это ни парадок­сально кажется на первый взгляд, шестилет­ки сознательно воспринимают символичес­кие записи, приведенные в программе для машины Поста (это подтверждается не толь­ко непосредственно нашей работой в течение 10 лет, но и всеми учителями, работавшими по пособию «Математика 0»). В частности, дети воспринимают и программы с ветвле­ниями, приведенными в примере 4. Это при­водит к гипотезе (которая, конечно, нуждает­ся в серьезной проверке), что, возможно, знакомство детей с работой на ЭВМ следует начинать еще в начальной школе.

Положительные результаты — повышение развивающего эффекта обучения, подготовка детей к изучению в дальнейшем информати­ки и общению с реальными вычислительными машинами — послужили основой для отра­жения наших экспериментов в учебной лите­ратуре для студентов педагогических инсти­тутов, будущих воспитателей детских садов и учителей начальных классов:

Практикум по методике начального обуче­ния математике.— М., 1984.

Формирование элементарных математиче­ских представлений у дошкольников.— М., 1988.

Методика начального обучения математи­ке.— М., 1988.

Для начальных классов использование игр, моделирующих машину Поста, рассмат­ривается впервые в настоящей статье.