Определение логарифма, логарифм произведения, степени, частного. Решение показательных и логарифмических уравнений и неравенств, страница 3

4.   Если , то функция принимает положительные значения при  и отрицательные, при . Если , то наоборот, при  значения функции будут положительными, а при  - отрицательными. Следовательно, при  график функции  расположен в первой и третьей координатных четвертях, при - во второй и четвёртой.

5.   Функция  является нечётной: она определена на симметричном множестве - интервале , и при любом удовлетворяет равенству , так как . Следовательно, график функции симметричен относительно начала координат.

6.   Функция  при является возрастающей, а при  - убывающей во всей области определения.

График функции представлен на рис. 27.

Рассмотрим функцию , где - чётное число, т. е.  (). Функция обладает следующими свойствами:

1.   Функция определена при всех значениях .

2.   Данная функция принимает неотрицательные значения при  () и неположительные значения при (). Область её значений - бесконечный промежуток  при  и бесконечный промежуток при .

3.   Если , то  при любом .

4.   Из двух последних свойств следует, что график функции проходит через начало координат и лежит выше оси  при  и ниже этой оси при .

5.   Функция является чётной, так как она определена на симметричном множестве, и при любом  выполняется равенство . Следовательно, график функции симметричен относительно оси ординат.

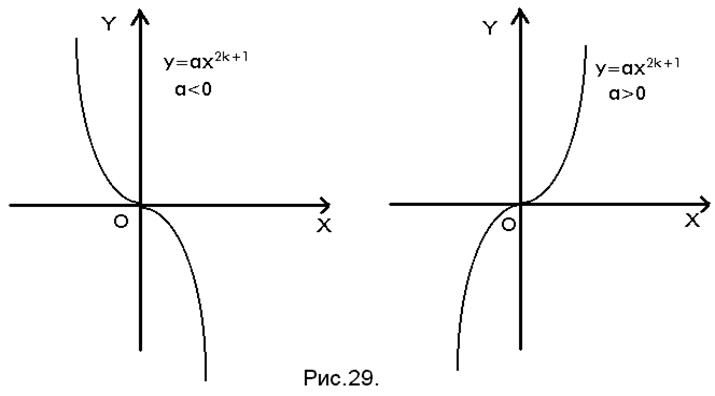
6.   Функция  в случае  убывает в интервале  и возрастает в интервале . При  она возрастает в интервале  и убывает в интервале .

График функции приведён на рис. 29.

ОПРЕДЕЛЕНИЕ  И  СВОЙСТВА ФУНКЦИИ    (  ГДЕ  > 0,  ¹ 1)  И ЕЁ ГРАФИК.

Функцию, заданную формулой   ( ), называют показательной.

Рассмотрим свойства показательной функции.

1.   Функция определена на всей числовой оси. .

2.   Функция принимает только положительные значения. . Действительно, любая степень положительного числа есть число положительное.

3.   Если , то  при  и  при . Это означает, что график функции ( ) расположен выше прямой при  и ниже её при .

4.   Если , то  при  и  при . Т. е. график функции ( ) расположен выше прямой при  и ниже её при .

5.   Функция  при  является возрастающей, а при  - убывающей.

6.   Каково бы ни было положительное число, существует такое число , что . Геометрически оно означает, что при любом положительном значении  график функции  обязательно пересекает прямую , причём только в одной точке.

7.   Если  неограниченно возрастает (), то при  также неограниченно возрастает(). Если  неограниченно убывает (),то принимает сколь угодно малые положительные значения ().

В случае  функция  неограниченно возрастает () при неограниченном убывании аргумента () и принимает сколь угодно малые положительные значения () при неограниченном возрастании аргумента ().

График функции  изображён на рис.30.

ОПРЕДЕЛЕНИЕ  И  СВОЙСТВА ФУНКЦИИ   (где  > 0,  ¹ 1)  И ЕЁ ГРАФИК.

     Определение. Логарифмической функциейназывается функция вида .

Свойства функции.

1.  Область определения: , что следует из определения логарифма.

2.  Область значений: .

3.  Чётность или нечётность. Функция не является чётной и не является нечётной, т. к. чётная или нечётная функция имеют область определения, симметричную относительно нуля.

4.  Нули функции: = 0, = 0, следовательно = 1. Значит, график функции пересекает ось  в точке с абсциссой 1.

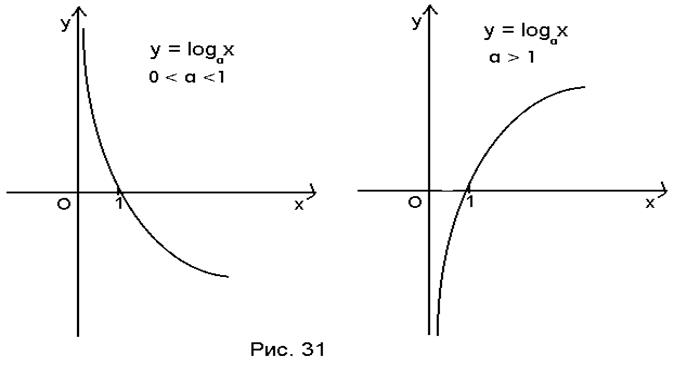
5.  Промежутки монотонности. Если > 1, то логарифмическая функция строго возрастает, если 0 < < 1, то она строго убывает.

Доказательство.1) Пусть  > 1. Возьмём два положительных числа  < , и докажем, что  <  . Обозначим =  и  =  .

По определению логарифма , . Если бы выполнялось неравенство  ³  , то по свойствам показательной функции выполнялось бы неравенство   ³ , т. е.  ³ , Это противоречит условию. Следовательно,  <  , что и требовалось доказать.

2) Пусть 0 < < 1. Возьмём два положительных числа  <  и покажем, что =  >   = . По определению логарифма ,

. Если  £  , то по свойству монотонности показательной функции выполняется  ³ , т. е.  ³ , что противоречит условию.   Следовательно,  <  , что и требовалось доказать.

6.  Если > 1, то при ® 0    ®  - ¥,  так как чтобы получить  надо  

возводить в степень с отрицательным показателем.

Если  0 < < 1, то при ® 0    ®  + ¥, так как чтобы получить  надо

 возводить в степень с положительным показателем.

График логарифмической функции.