Показательнымназывают уравнение, содержащее переменную в показателе степени, т. е. уравнение вида
![]() , где
, где
![]() и
и ![]() -
действительные числа (
-
действительные числа (![]() > 0,
> 0, ![]() ¹ 1,
¹ 1, ![]() > 0),
> 0), ![]() и
и ![]() - некоторые функции переменной
- некоторые функции переменной
![]() . Так как
. Так как ![]() (основное
логарифмическое тождество), то уравнение
(основное
логарифмическое тождество), то уравнение ![]() можно
привести к виду
можно
привести к виду ![]() , где
, где ![]() .
.
Решение показательных уравнений основано на следующем утверждении
Теорема. Показательное уравнение
![]()
равносильно уравнению
![]() .
.
Простейшие показательные уравнения
получаются при ![]() . Они имеют соответственно
вид :
. Они имеют соответственно
вид :
![]() .
.
Первое
из этих уравнений равносильно уравнению ![]() ,
второе - уравнению
,
второе - уравнению ![]() .
.
Если задано уравнение
![]() (
(![]() > 0,
> 0, ![]() ¹ 1,
¹ 1, ![]() > 0,
> 0, ![]() ¹
¹ ![]() ), то
его можно привести к уравнению вида
), то
его можно привести к уравнению вида
![]() , где
, где ![]() .
.
Это уравнение равносильно уравнению
![]() .
.
Показательное уравнение
![]() , где
, где
![]() > 0,
> 0, ![]() ¹ 1,
¹ 1, ![]() - заданная функция, решают подстановкой
- заданная функция, решают подстановкой ![]()
![]() . Для
. Для ![]() получают уравнение
получают уравнение
![]() .
.
Если
![]() - корни этого уравнения, удовлетворяющие
условию
- корни этого уравнения, удовлетворяющие
условию ![]() , то корнями уравнения
, то корнями уравнения ![]() будут все корни уравнения
будут все корни уравнения
![]() , где
, где
![]() , т. е. корни уравнений
, т. е. корни уравнений
![]()
При решении показательных неравенств следует помнить, что функция ![]() (
(![]() >
0,
>
0, ![]() ¹ 1) является
возрастающей, если
¹ 1) является
возрастающей, если ![]() > 1, и убывающей, если 0
<
> 1, и убывающей, если 0
< ![]() < 1 . Поэтому неравенство вида
< 1 . Поэтому неравенство вида
![]()
на
пересечении областей определения функций ![]() и
и ![]() при
при ![]() >
1 равносильно неравенству
>
1 равносильно неравенству
![]() , а
при 0 <
, а
при 0 < ![]() < 1 - неравенству
< 1 - неравенству
![]() .
.
Таким же образом
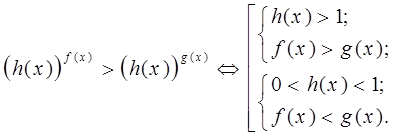
Если решается неравенство вида
![]() (
(![]() > 0), то
при
> 0), то
при ![]() £ 0 решением
неравенства будет любое
£ 0 решением
неравенства будет любое ![]() ; если же
; если же ![]() > 0, то данное неравенство равносильно
неравенству
> 0, то данное неравенство равносильно
неравенству
![]() , когда
, когда
![]() > 1, и неравенству
> 1, и неравенству
![]() , когда
0 <
, когда
0 < ![]() < 1. Если
< 1. Если ![]() = 1, то получаем числовое неравенство
= 1, то получаем числовое неравенство
![]() .
.
Неравенство вида
![]() (
(![]() > 0) при
> 0) при
![]() £ 0 решений не имеет,
а при
£ 0 решений не имеет,
а при ![]() > 0 равносильно совокупности систем
> 0 равносильно совокупности систем
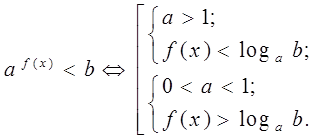
Неравенство вида
![]() ( или < 0)
( или < 0)
с
помощью подстановки ![]() > 0 сводится к квадратному
неравенству
> 0 сводится к квадратному
неравенству
![]() ( или < 0)
( или < 0)
и получаем в результате подстановки совокупности
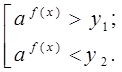
или системы неравенств
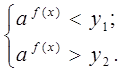
где
![]() - корни квадратного трёхчлена
- корни квадратного трёхчлена ![]() .
.
Логарифмическим уравнением называют уравнение, содержащее переменную под знаком логарифма:
![]()
Функция
![]() должна удовлетворять условиям:
должна удовлетворять условиям: ![]() > 0,
> 0, ![]() ¹ 1; функции
¹ 1; функции ![]() и
и ![]() должны быть положительными. В этих
условиях справедливо утверждение
должны быть положительными. В этих
условиях справедливо утверждение
Теорема. Логарифмическое уравнение
![]()
равносильно уравнению
![]() .
.
В общем случае это уравнение равносильно системе
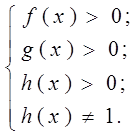
В частном случае, когда ![]() , причём
, причём ![]() > 0,
> 0, ![]() ¹1 это
уравнение принимает вид
¹1 это
уравнение принимает вид
![]()
что равносильно системе
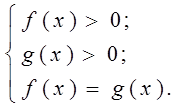
При решении уравнений вида
![]()
где
![]() - многочлен, вводится новая переменная
- многочлен, вводится новая переменная ![]()
Уравнения, содержащие переменную в основании и в показателе степени, решают, как правило, логарифмированием обеих частей. Если в показателе степени содержится логарифм, то обе части уравнения логарифмируют по основанию этого логарифма.
При решении логарифмических неравенств следует обращать внимание на то, что при
основании, большем единице, логарифмическая функция монотонно возрастает, а при
положительном основании, меньшем единицы, - монотонно убывает. В связи с этим
при ![]() > 1 неравенство
> 1 неравенство
![]()
равносильно неравенству
![]() , а
при 0 <
, а
при 0 < ![]() < 1 - равносильно
неравенству
< 1 - равносильно
неравенству
![]()
в области определения неравенства.
Аналогично
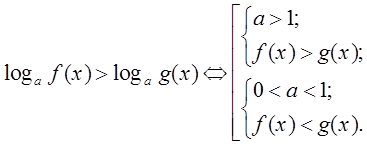
Рассмотрим неравенства вида
![]() ( или < 0);
( или < 0); ![]() (или <
(или < ![]() ) где
) где
![]() - некоторое число.
- некоторое число.
Решение каждого неравенства сводится к решению совокупности двух систем неравенств, равносильной данному неравенству в области его определения.
Используя свойство логарифмов о том, что логарифм положителен, если логарифмируемое число и основание логарифма лежат по одну сторону от единицы, и логарифм отрицателен, если они лежат по разные стороны от единицы, можем записать, что неравенство
![]()
равносильно совокупности систем неравенств
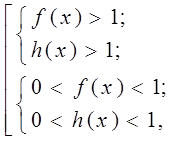
а неравенство
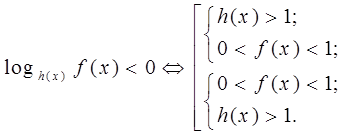
Неравенство
![]()
можно заменить неравенством
![]()
и использовать свойство монотонности логарифмической функции. Поэтому неравенство
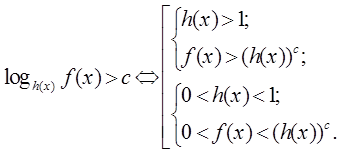
Неравенство
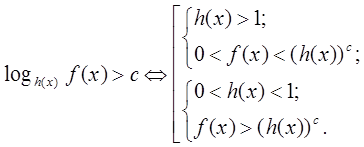
СВОЙСТВА ФУНКЦИИ ![]() (ГДЕ
(ГДЕ ![]() ) И ЕЁ ГРАФИК.
) И ЕЁ ГРАФИК.
Функция
вида ![]() , где
, где ![]() ,
, ![]() - действительные числа называется степенной.
- действительные числа называется степенной.
Будем рассматривать случай, когда ![]() , где
, где ![]() -
натуральное число. В этом случае функция
-
натуральное число. В этом случае функция ![]() определена
при всех значениях аргумента
определена
при всех значениях аргумента ![]() .
.
Рассмотрим сначала функцию ![]() , где
, где ![]() -
нечётное число, т. е.
-
нечётное число, т. е. ![]() (
(![]() ).
Функция
).
Функция ![]() обладает следующими свойствами:
обладает следующими свойствами:
1. Функция ![]() определена при всех
значениях
определена при всех
значениях ![]() ,
, ![]() .
.
2. Множество значений функции также равно ![]() .
.
3. Если ![]() , то
, то ![]() ; график функции проходит через начало
координат.
; график функции проходит через начало
координат.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.