ОПРЕДЕЛЕНИЕ ЛОГАРИФМА. ЛОГАРИФМ ПРОИЗВЕДЕНИЯ, СТЕПЕНИ, ЧАСТНОГО.
Определение. Логарифмом
положительного числа ![]() по основанию
по основанию ![]() (
(![]() )
называется показатель степени, в которую надо возвести
)
называется показатель степени, в которую надо возвести ![]() ,
чтобы получить
,
чтобы получить ![]() .
.
В записи ![]() число
число ![]() является
основанием степени,
является
основанием степени, ![]() - показателем,
- показателем, ![]() - степенью. Число
- степенью. Число ![]() -
это показатель степени, в которую надо возвести основание
-
это показатель степени, в которую надо возвести основание ![]() , чтобы получить число
, чтобы получить число ![]() . Следовательно,
. Следовательно, ![]() -
это логарифм числа
-
это логарифм числа ![]() по основанию
по основанию ![]() :
:
![]() .
.
Можно сказать, что формулы ![]() и
и ![]() равносильны,
выражают одну и ту же связь между числами
равносильны,
выражают одну и ту же связь между числами ![]() ,
, ![]() и
и ![]() (при
(при ![]() > 0,
> 0, ![]() ¹ 1,
¹ 1, ![]() > 0). Число
> 0). Число ![]() -
произвольно, никаких ограничений на показатель степени не накладывается.
-
произвольно, никаких ограничений на показатель степени не накладывается.
Равенство
![]()
называется основным логарифмическим тождеством.
Представляя в равенстве ![]() выражение
выражение ![]() в
виде степени, получим ещё одно тождество
в
виде степени, получим ещё одно тождество
![]() .
.
Теорема. Для чисел ![]() > 0,
> 0, ![]() > 0,
> 0, ![]() > 0,
> 0,
![]() ¹
1 верны следующие тождества, выражающие свойства логарифмов:
¹
1 верны следующие тождества, выражающие свойства логарифмов:
1) ![]() ,
т. е. логарифм произведения равен сумме логарифмов множителей;
,
т. е. логарифм произведения равен сумме логарифмов множителей;
2) 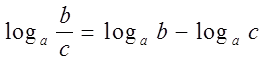 , т. е. логарифм дроби равен
разности логарифмов числителя и знаменателя;
, т. е. логарифм дроби равен
разности логарифмов числителя и знаменателя;
3) ![]() , т. е. логарифм степени равен
показателю степени, умноженному на логарифм основания.
, т. е. логарифм степени равен
показателю степени, умноженному на логарифм основания.
Доказательство. 1) Пусть ![]() ,
, ![]() . По основному логарифмическому тождеству
. По основному логарифмическому тождеству ![]() ,
, ![]() .
Перемножим эти равенства:
.
Перемножим эти равенства: ![]() .
По свойству степеней
.
По свойству степеней ![]() , т. е.
, т. е. ![]() .
По определению логарифма
.
По определению логарифма
![]() , т. е.
, т. е.
![]() , что и требовалось доказать.
, что и требовалось доказать.
2) Пусть ![]() ,
, ![]() . По
основному логарифмическому тождеству:
. По
основному логарифмическому тождеству: ![]() ,
, ![]() . Тогда
. Тогда
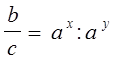 .
.
По свойству степеней
![]() , т. е.
, т. е.
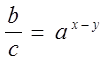 .
.
По определению логарифма
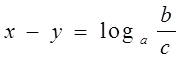 , т. е.
, т. е.
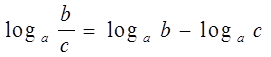 , что и требовалось доказать.
, что и требовалось доказать.
3) Пусть ![]() . По основному логарифмическому тождеству
. По основному логарифмическому тождеству ![]() . Тогда
. Тогда
![]() .
.
По определению логарифма
![]() , т. е.
, т. е. ![]() .
Теорема доказана.
.
Теорема доказана.
ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ. НАТУРАЛЬНЫЕ ЛОГАРИФМЫ. ФОРМУЛА ПЕРЕХОДА ОТ ОДНОГО ОСНОВАНИЯ К ДРУГОМУ.
Если в равенстве ![]() основание
основание ![]() равно 10, то логарифм называется десятичным
и обозначается
равно 10, то логарифм называется десятичным
и обозначается ![]() . Если же в равенстве
. Если же в равенстве ![]() основание
основание ![]() равно
равно ![]() , где
, где ![]() -
бесконечная непериодическая десятичная дробь, то логарифм называется натуральным
и обозначается
-
бесконечная непериодическая десятичная дробь, то логарифм называется натуральным
и обозначается ![]() . Свойства десятичных и
натуральных логарифмов аналогичны свойствам обыкновенных логарифмов и они
отличаются лишь формой записи.
. Свойства десятичных и
натуральных логарифмов аналогичны свойствам обыкновенных логарифмов и они
отличаются лишь формой записи.
Рассмотрим некоторые свойства логарифмов:
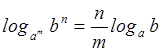 .
В частности
.
В частности 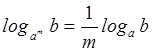 ,
, Между
логарифмами некоторого положительного числа ![]() с двумя
разными основаниями
с двумя
разными основаниями ![]() и
и ![]() существует
зависимость, которую можно выразить формулой
существует
зависимость, которую можно выразить формулой
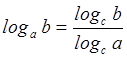 .
.
Эту формулу называют формулой
перехода от одного основания к другому. В частности из неё следует, что 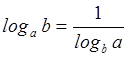 или
или ![]() , кроме
того
, кроме
того 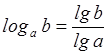 ,
, 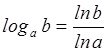 .
.
ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ ВЫРАЖЕНИЙ, СОДЕРЖАЩИХ ЛОГАРИФМЫ.
Используя свойства логарифмов, можно представить логарифм некоторого выражения, составленного из положительных чисел с помощью операций умножения, деления и возведения в степень, в виде суммы логарифмов входящих в него чисел.
Такое преобразование называют логарифмированием.
Пример 1. Прологарифмировать выражение по основанию ![]() (
(![]() ).
).
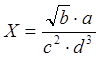 .
.
Решение. Применяя свойства логарифмов, получим
![]()
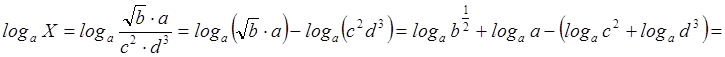
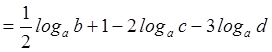 .
.
Во многих случаях приходится решать обратную задачу, т. е. находить выражение, логарифм которого представлен через логарифмы некоторых чисел. Такое преобразование называют потенцированием.
Пример 2. Найти ![]() , если
, если
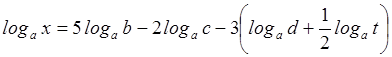 .
.
Решение. Используя свойства логарифмов, получаем:
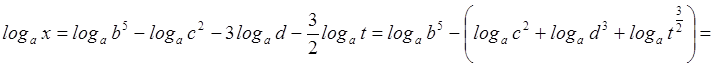
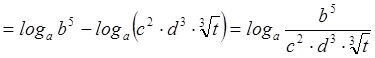 .
Таким образом
.
Таким образом 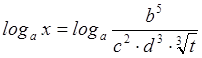 . Отсюда
. Отсюда 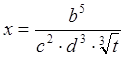 .
.
РЕШЕНИЕ ПОКАЗАТЕЛЬНЫХ И ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.