С другой стороны в результате преобразования s уравнение Шредингера должно приобрести вид
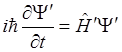 , (1.95)
, (1.95)
где ![]() - новый оператор
Гамильтона системы. Как видно из двух последних формул оператор Гамильтона
преобразуется по формуле
- новый оператор
Гамильтона системы. Как видно из двух последних формул оператор Гамильтона
преобразуется по формуле
![]() . (1.96)
. (1.96)
Если s – преобразование
симметрии системы, то ![]() . Тогда, умножая обе
стороны равенства (1.96) на оператор
. Тогда, умножая обе
стороны равенства (1.96) на оператор ![]() , получим
, получим
![]() .
(1.97)
.
(1.97)
Итак, в случае преобразования симметрии оператор ![]() должен коммутировать с оператором
Гамильтона системы.
должен коммутировать с оператором
Гамильтона системы.
Однородность времени.
Однородность времени означает инвариантность системы по
отношению к временному сдвигу ![]()
![]() . (1.98)
. (1.98)
Считая сдвиг бесконечно малым, найдём оператор
преобразования ![]() . С учётом (1.92) получим
. С учётом (1.92) получим
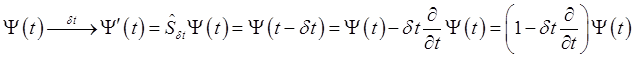 .
.
Из последней формулы следует, что оператор сдвига во времени имеет вид
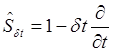 . (1.99)
. (1.99)
Из свойства однородности времени вытекает, что оператор
Гамильтона замкнутой системы должен коммутировать с оператором ![]() . Это возможно только в том случае, когда
оператор
. Это возможно только в том случае, когда
оператор ![]() не зависит явно от времени.
Последнее, как следует из формулы (1.78), означает, что энергия системы сохраняется.
не зависит явно от времени.
Последнее, как следует из формулы (1.78), означает, что энергия системы сохраняется.
Однородность пространства.
Совершим малый сдвиг системы в
пространстве, который описывается вектором ![]()
![]() . (1.100)
. (1.100)
Оператор сдвига определяется из следующей выкладки
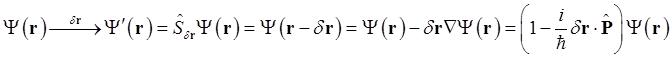 и равен
и равен
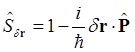 (1.101)
(1.101)
Из свойства однородности пространства, таким образом, следует, что оператор импульса должен коммутировать с оператором Гамильтона. Следовательно, импульс замкнутой системы сохраняется во времени.
Изотропность пространства.
Введём малый аксиальный вектор ![]() и совершим поворот системы вокруг этого
вектора на угол
и совершим поворот системы вокруг этого
вектора на угол ![]() . Координаты системы при
этом получат приращение
. Координаты системы при
этом получат приращение
![]() . (1.102)
. (1.102)
Оператор соответствующего преобразования в пространстве волновых функций определяется выражением
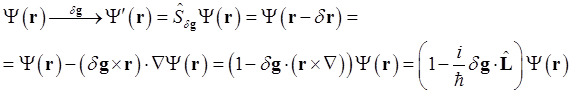
и равен
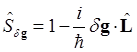 , (1.103)
, (1.103)
где ![]() -
оператор момента импульса. Рассуждая аналогично предыдущему случаю, приходим к
выводу о сохранении момента
импульса замкнутой системы.
-
оператор момента импульса. Рассуждая аналогично предыдущему случаю, приходим к
выводу о сохранении момента
импульса замкнутой системы.
Симметрия правого и левого.
Указанная симметрия проявляется в инвариантности гамильтониана системы по отношению к инверсии её координат. В отличие от рассмотренных ранее преобразований симметрии данное преобразование является дискретным и в классической физике не приводит к каким-либо законам сохранения. В квантовой механике симметрия правого и левого приводит к ещё одному закону сохранения.
Введём оператор инверсии ![]() , действие которого сводится к перемене
знака всех координат
, действие которого сводится к перемене
знака всех координат
![]() (1.104)
(1.104)
Найдём собственные функции и собственные значения оператора инверсии. Собственные функции должны удовлетворять уравнению
![]() , (1.105)
, (1.105)
где ![]() -
собственное значение оператора. Подействуем оператором инверсии на обе стороны
выражения (1.105). С учётом того, что двукратное применение оператора инверсии
оставляет функцию неизменной, получим
-
собственное значение оператора. Подействуем оператором инверсии на обе стороны
выражения (1.105). С учётом того, что двукратное применение оператора инверсии
оставляет функцию неизменной, получим
![]() (1.106)
(1.106)
Как видно из последнего равенства ![]() может принимать только два значения 1 или
-1. Соответственно, собственные функции разбиваются на два типа. Функции,
принадлежащие собственному значению +1, оказываются чётными
может принимать только два значения 1 или
-1. Соответственно, собственные функции разбиваются на два типа. Функции,
принадлежащие собственному значению +1, оказываются чётными
![]() , (1.107)
, (1.107)
а собственному значению -1, нечётными
![]() . (1.108)
. (1.108)
В силу симметрии правого и левого, собственные значения оператора инверсии, а следовательно и указанные свойства волновых функций, должны сохраняться во времени. Свойство волновой функции системы оставаться чётной (или нечётной) с течением времени называется законом сохранения чётности.
Все рассмотренные выше законы сохранения имеют место для замкнутой системы. При наличии внешнего поля, у которого имеются некоторые элементы симметрии, могут иметь место отдельные законы сохранения, связанные с соответствующими преобразованиями симметрии. В частности, если потенциальная функция не зависит явно от времени, имеет место закон сохранения энергии системы. Неизменность потенциальной функции при сдвиге вдоль (повороте вокруг) некоторой оси, ведёт к сохранению проекции импульса (момента импульса) на данную ось.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.