Изменение средних значений, наблюдаемых во времени. Соотношение неопределённости для энергии. Теоремы Эренфеста и предельный переход к классической механике. Законы сохранения и их связь с симметрией пространства, времени и внешнего поля

Лекция №6.

План лекции:

Изменение средних значений наблюдаемых во времени

Соотношение неопределённости для энергии

Теоремы Эренфеста и предельный переход к классической механике

Законы сохранения и их связь с симметрией пространства, времени и внешнего поля

Ключевые слова:

теорема о сохранении наблюдаемых

соотношения неопределённости для энергии и времени

естественная ширина уровня

теоремы Эренфеста законы сохранения:

энергии импульса

момента импульса

чётности

Изменение средних значений наблюдаемых во времени

Зависимость волновой функции от времени приводит к тому, что с течением времени изменяются средние значения наблюдаемых, даже если оператор этих наблюдаемых не зависит явно от времени. По определению среднего

.

Найдём производную по времени от

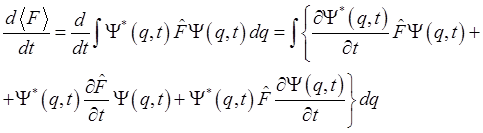
Выражая производные по времени от волновых функций из уравнений (1.68) и (1.69), а также, воспользовавшись свойством эрмитовости оператора Гамильтона  (1.14), получим

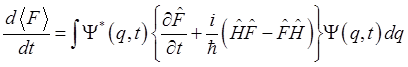                    (1.77).

Полученная формула выражает закон сохранения наблюдаемых в квантовой механике.

Среднее значение наблюдаемой сохраняется, если её оператор не зависит явно от времени и коммутирует с оператором Гамильтона.

Рассмотрим теперь вопрос об определении скорости изменения наблюдаемых в квантовой механике. Величину нельзя ввести как предел, к которому стремится отношение  при , так как этот предел просто не существует. Сопоставим этой величине оператор , который определим следующим образом. Будем считать, что производная по времени от среднего значения наблюдаемой равна среднему значению производной по времени от наблюдаемой 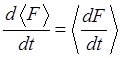. Отсюда, имея в виду, что

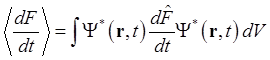
получим

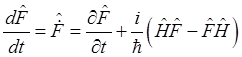.                                     (1.78)

Соотношение неопределённости для энергии

Перепишем соотношение (1.78) в виде

.

Тогда, применяя доказанную ранее теорему (см. формулы (1.42) и (1.46)), получим

.

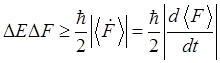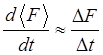Пусть - время, в течение которого среднее значение наблюдаемой F меняется на величину равную среднеквадратичной флуктуации . Тогда полагая  получим

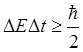.                                                     (1.79)

Полученное неравенство носит название соотношения неопределённости для энергии и времени. Несмотря на внешнее сходство,оно по своему смыслу отличается от аналогичных соотношений для координаты и импульса. В частности оно не запрещает иметь определённое значение энергии в данный момент времени. Пусть, например, среднее значение координаты частицы меняется на величину своей среднеквадратичной флуктуации за время . Тогда неопределённость энергии этой частицы определяется соотношением (1.79). Рассмотрим систему, находящуюся в состоянии, которое распадается за время . Такое состояние принято называть квазистационарным, а - временем жизни этого состояния. Тогда, подставив значение в формулу (1.79) можно найти неопределённость в значении энергии состояния. Величина , которая связана с временем жизни соотношением

                                                        (1.80)

называется естественной шириной энергетического уровня.

Теоремы Эренфеста и предельный переход к классической механике

Найдём производные по времени от , воспользовавшись для этого выражением (1.77). Вычисление коммутаторов оператора Гамильтона с операторами координаты и импульса даёт

,

      .

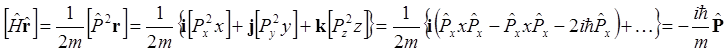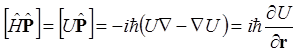Подставляя вычисленные коммутаторы в формулу (1.77), получим

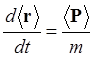                            ,           (1.81)                  

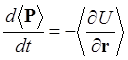  .                              (1.82)

Как видно из полученных формул известные соотношения классической механики выполняются и в квантовой механике, но для средних значений наблюдаемых. В этом и состоит смысл теорем Эренфеста. Дифференцируя по времени правую и левую сторону равенства (1.80) получим выражение

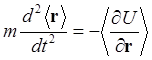                 ,           (1.83)

которое можно назвать квантовым уравнением Ньютона. Это уравнение имеет принципиальное отличие от своего классического аналога. В классической механике ускорение частицы определяется силой, действующей в той точке, где находится частица. Стоящее же в правой части уравнения (1.83) выражение представляет собой квантовомеханическое усреднение по всему пространству. Для перехода к классическому пределу необходимо заменить 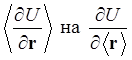. Рассмотрим условия такого перехода и в целях упрощения ограничимся одномерным случаем. Разложим стоящую под знаком усреднения величину в ряд Тейлора по отклонению координаты частицы от её среднего значения

  .

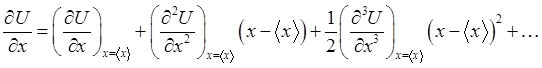Результат разложения не изменится, если в производных сначала подставить вместо x  его среднее значение, а затем взять производную по . Так, например, вместо 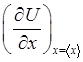 будем иметь ,  где U  теперь надо рассматривать как функцию . Считая отклонения координаты от среднего малыми величинами, ограничимся первыми тремя членами разложения. Тогда после усреднения получим