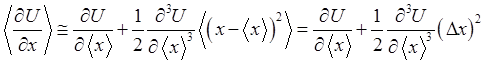 . (1.84)
. (1.84)
При усреднении было учтено очевидное
равенство ![]() , а для среднеквадратичной
флуктуации координаты введено обозначение
, а для среднеквадратичной
флуктуации координаты введено обозначение ![]() .
Из полученной формулы видно, что квантовое уравнение движения переходит в
классическое
.
Из полученной формулы видно, что квантовое уравнение движения переходит в
классическое
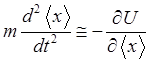 , (1.85)
, (1.85)
если можно пренебречь вторым слагаемым в формуле (1.84). Для этого должно выполняться условие
![]()
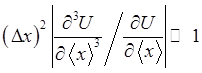 . (1.86)
. (1.86)
Выполнению этого условия способствует локализация частицы в ограниченной области пространства и достаточно гладкие потенциальные функции.
Классическая
механика предполагает также квадратичную зависимость кинетической энергии от
импульса частицы, то есть в данном случае для средних значений должно
выполняться равенство 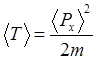 . Вместо этого в
квантовой механике имеем
. Вместо этого в
квантовой механике имеем 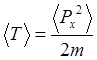 . Условие
перехода от квантовой к классической формуле видно из следующих простых
выкладок
. Условие
перехода от квантовой к классической формуле видно из следующих простых
выкладок
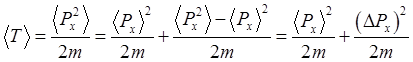 , где
, где ![]() -
среднеквадратичная флуктуация импульса. Переход к классическому выражению
возможен при условии, что
-
среднеквадратичная флуктуация импульса. Переход к классическому выражению
возможен при условии, что
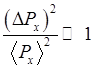 , (1.87)
, (1.87)
для выполнения которого нужно, чтобы
частица обладала достаточно большим импульсом. Выражения (1.86)
и (1.87) можно объединить. Перемножая почленно левые и
правые части неравенств, и учитывая, что ![]() ,
получим
,
получим
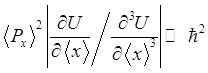 или
или
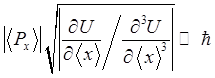 .
(1.88)
.
(1.88)
Итак, стоящая в левой части неравенства величина, имеющая размерность момента, должна быть намного больше постоянной Планка.
В квантовой механике момент
импульса обладает дискретным спектром, а его проекции могут изменяться только
на величину кратную постоянной Планка (см. лекцию №4). Фактом квантования
момента можно пренебречь и считать спектр его значений непрерывным, если
среднее значение момента намного больше ![]() .
Таким образом, переход к классическому описанию возможен, если все величины,
характеризующие систему и имеющие размерность момента намного больше постоянной
Планка.
.
Таким образом, переход к классическому описанию возможен, если все величины,
характеризующие систему и имеющие размерность момента намного больше постоянной
Планка.
Законы сохранения и их связь с симметрией пространства, времени и внешнего поля.
Особую роль в квантовой механике играют физические величины, операторы которых не зависят от времени и коммутируют с оператором Гамильтона. Выше было показано, что среднее значение таких величин сохраняется. Существует связь между законами сохранения и симметрией пространства, времени и внешнего поля. Совокупность экспериментальных фактов свидетельствует о том, что пространство является однородным и изотропным, а время однородным. Кроме того, во всех фундаментальных физических взаимодействиях, за исключением «слабого» имеет место симметрия правого и левого. Симметрия системы проявляется в инвариантности уравнений теории по отношению к тем или иным преобразованиям координат и времени. При этом неизменным должно оставаться в данном случае не только уравнение Шредингера, но и оператор Гамильтона системы. Преобразования, которые оставляют гамильтониан системы инвариантным называются преобразованиями симметрии данной системы
Прежде, чем
рассматривать преобразования симметрии, определим, как меняются волновые
функции системы при произвольных преобразованиях координат. Пусть s - некоторое преобразование координат, в результате
которого точка системы r переходит в ![]() , так что
, так что
![]() . (1.89)
. (1.89)
При переходе к новым координатам вид волновой функции должен
измениться. Это изменение можно описать с помощью оператора ![]() , который является отображением
преобразования координат s на пространство
волновых функций:
, который является отображением
преобразования координат s на пространство
волновых функций:
![]() . (1.90)
. (1.90)
При этом должно иметь место равенство
![]() , (1.91)
, (1.91)
поскольку ![]() - координаты
одной и той же точки системы, соответственно, до и после преобразования.
Подставляя в (1.91) выражение (1.90),
получим
- координаты
одной и той же точки системы, соответственно, до и после преобразования.
Подставляя в (1.91) выражение (1.90),
получим
![]() , (1.92)
, (1.92)
где символом ![]() обозначено
обратное преобразование координат
обозначено
обратное преобразование координат ![]() . Из последней
формулы вытекает, что действие оператора на волновую функцию сводится к
обратному преобразованию над её аргументом.
. Из последней
формулы вытекает, что действие оператора на волновую функцию сводится к
обратному преобразованию над её аргументом.
Рассмотрим
теперь, как изменится уравнение Шредингера, если провести преобразование s над координатами системы. Для этого подействуем
оператором ![]() на обе стороны уравнения
Шредингера и вставим в правую его часть единичный оператор
на обе стороны уравнения
Шредингера и вставим в правую его часть единичный оператор ![]() , который не меняет стоящее справа от него
выражение (
, который не меняет стоящее справа от него
выражение (![]() - оператор обратного по отношению
к оператору
- оператор обратного по отношению
к оператору ![]() преобразования).
преобразования).
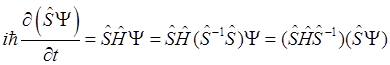 . (1.93)
. (1.93)
С учётом формулы (1.90) получим
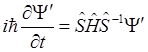 . (1.94)
. (1.94)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.