Усадочные процессы при формировании отливок, страница 7

На графике вертикальная координатная ось представляет сразу две величины изменения температуры и усадочных деформаций, так как приближенно можно считать, что деформации находятся в линейной зависимости от температуры. Температура перехода из пластического в упругое состояние приближенно оценивается

, где Т₀ – температура затвердевания.

Для упрощения будем считать, что массивная и тонкая части бруса одновременно перешли из жидкого состояния в твердое при температуре Т₀. Но в дальнейшем, начиная с температуры Т₀, тонкая и массивная части бруса охлаждаются с разными скоростями и в различное время проходят стадию перехода из пластического состояния в упругое: тонкая часть ко времени t₁, а массивная – t₂. До момента времени t₁ обе части бруса находятся в пластическом состоянии и общая усадка бруса протекает по пунктирной кривой, равноудаленной от величины усадки тонкой и массивной части. Но начиная с момента времени t₁ и до времени t₂ тонкая часть бруса находится в упругом состоянии, а массивная часть остается в пластическом. Поэтому кинетическая кривая усадки DL всего бруса располагается параллельно кривой усадки тонкой части. Но с момента времени t₂ и массивная часть перешла в упругое состояние и кинетическая кривая усадки бруса (на рис. 82 не изображена) располагается между кривыми усадки тонкой и массивной частей и к концу охлаждения при 20°С величина усадки бруса определится положением точки l₀. Чтобы оценить величину и характер напряжений в брусе после полного охлаждения в момент t₂ мысленно отделим тонкую часть от массивной и предоставим гипотетически возможность охлаждаться и сокращаться в размерах за счет усадки самостоятельно. Кинетическая кривая усадки тонкой части DL_F располагается параллельно кривой Т_F, и при 20°С длина тонкой части определялась бы точкой l₂. В свою очередь кинетическая кривая усадки массивной части DL_f располагается параллельно кривой Т_f, и при 20°С длина массивной части определялась бы положением точки l₁. Таким образом, отрезок прямой l₂ – l₀ представляет упругую деформацию тонкой части, а отрезок прямой l₀ – l₁ – упругую деформацию массивной части. Из графического представления кинетики охлаждения и усадочных деформаций бруса, очевидно, что в массивной части остаточные температурные напряжения будут растягивающими, а в тонкой части сжимающими.

По аналогии с методикой расчета временных температурных напряжений величина остаточных напряжений определится:

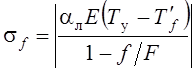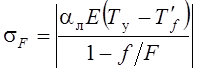; , где  – температура тонкой части бруса к моменту времени t₂, когда массивная часть бруса перешла в упругое состояние.

Внутренние температурные напряжения могут суммироваться с фазовыми напряжениями или напряжениями, вызванными затрудненной усадкой, если они совпадают по знаку. Если же знак напряжений: растяжение или сжатие от разных причин различен, то соответственно снижается величина внутренних напряжений.

Под действием внутренних напряжений могут происходить коробления, приводящие к искажению размеров отливок, а также трещины и даже полное разрушение отливок.

Коробления отливок происходят, когда величина внутренних напряжений на какой-либо стадии охлаждения отливки достигнет величины предела пропорциональности, в результате чего происходят упругие или пластические деформации.

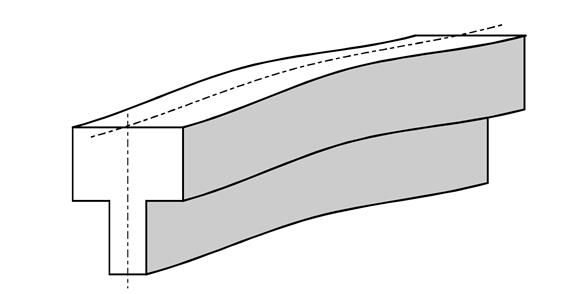
Рис. 84. Схема коробления отливки «брус» на стадии образования временных температурных напряжений (сжимающие – в массивной части, растягивающие – в тонкой части).

На рис. 84 схематично изображено коробление бруса под действием временных температурных напряжений, когда в массивной части развиваются сжимающие, а в тонкой части – растягивающие напряжения. Если изображенный изгиб бруса не выйдет из пределов упругих деформаций, то затем отливка примет первоначальную форму.