Усадочные процессы при формировании отливок, страница 6

Плотность структурных составляющих сплавов Fe-С

В связи с неравномерностью охлаждения отдельных частей отливок в них могут оказаться на разных стадиях перекристаллизации (фазовом переходе в твердом состоянии) различные структурные составляющие, а значит неодинаково будут протекать изменения объемов и линейных размеров. И в наибольшей степени это проявится при графитизации чугунов – «рост» размеров. Деформации и напряжения, связанные с этим явлением получили название фазовых.

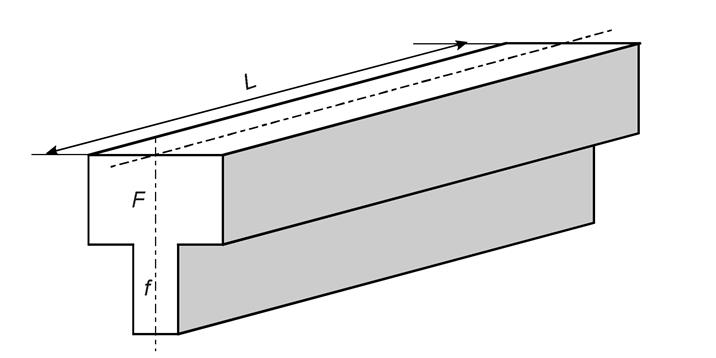
Рис. 81. Отливка «брус», у которой сечение F >> f

И все-таки температурные напряжения в отливках являются преобладающими, они имеют место на всех сплавах и на отливках с разной толщиной стенок, с тепловыми узлами. Рассмотрим развитие температурных напряжений в твердой отливке типа «брус» постоянного поперечного сечения, но характеризующегося с большой разнотолщинностью стенок (рис. 81). Естественно, что массивная часть бруса «F» охлаждается значительно медленнее, чем тонкая часть «f».

Температурные напряжения в отливках классифицируют на временные, развивающиеся на стадии промежуточного охлаждения твердой отливки, и остаточные, имеющие место в полностью охлажденной отливке. Временные и остаточные напряжения могут существенно различаться не только по величине, но и по знаку.

Вначале оценим временные напряжения в отливке «брус» для промежуточного интервала времени t, как это схематично представлено на рис. 82. При охлаждении с некоторой одинаковой исходной температуры Т₀ ко времени t₁ массивная часть охладится до температуры Т_F, а тонкая часть до температуры Т_f. Здесь очевидно, что Т_F > Т_f. По этой причине если бы тонкая и массивная части бруса не были жестко связаны друг с другом, то за счет усадки сократились бы на неодинаковую величину: тонкая часть на , а массивная часть на величину ; при этом . Но поскольку обе части бруса жестко связаны между собой, то они сократятся на одинаковую величину, а разница в температурных изменениях размеров будет уравновешена возникшими внутренними напряжениями. Если принять, что коробления бруса не происходит, то величина напряжений по закону Гука пропорциональна относительной величине упругих деформаций:

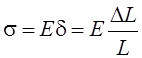, где Е – величина модуля упругости материала отливки при соответствующей температуре.

Составим уравнение баланса деформаций тонкой и массивной частей бруса:

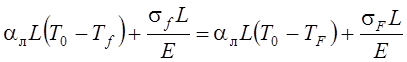, где s_f и s_F – величина напряжений соответственно в тонкой и массивной частях.

Поскольку в одном вышеприведенном алгебраическом выражении две неизвестных величины: s_f и s_F, запишем еще одно уравнение равновесия сил в тонкой и массивной частях:

.

После решения системы двух алгебраических уравнений получим:

; .

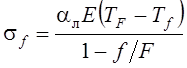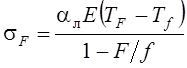Здесь величины напряжений s_f и s_F различны как по величине, так и по знаку. Очевидно, что временные температурные напряжения в массивной части бруса будут сжимающими, а в тонкой части растягивающими, так как тонкая часть без силового воздействия массивной части сократилась бы на большую величину, а массивная часть бруса без силового воздействия тонкой сократилась бы на меньшую величину.

Остаточные напряжения в полностью охлажденной отливке будут отличаться не только по величине, но возможно и по знаку. Для расчета остаточных напряжений в отливке «брус» проанализируем кинетику деформаций в обеих частях бруса с учетом разницы температур и неодновременности перехода обеих частей из пластического в упругое состояние, как это схематично представлено на рис. 83.