Геометрическая конфигурация усадочной раковины и ее расположение зависит от условий и направленности затвердевания отливки. При строго направленном затвердевании снизу вверх отливки постоянного поперечного сечения усадочная раковина полностью располагается в верхней части и представляет собой уменьшенную высоту отливки по сравнению с высотой формы, заполненной расплавом. В этом случае не происходит затвердевание металла на боковых поверхностях.
А теперь рассмотрим другой случай, когда затвердевание отливки происходит только с боковой поверхности и полностью отсутствует затвердевание отливки в направлении ее вертикальной оси. Для цилиндрической отливки радиусом R и высотой Н форму усадочной раковины рассчитаем для ряда частных условий: а) отливка формируется из чистого металла; б) металл заливается в форму без перегрева, т.е. температура заливки равна температуре затвердевания.
За некоторый промежуток времени после заливки на боковой поверхности
затвердеет корка металла толщиной x
(рис. 75). При этом незатвердевший металл будет представлять цилиндр радиусом r = R – x и высотой h.
Определенно, что h < Н в результате
опускания уровня металла по причине усадки. За элементарный промежуток времени dt толщина затвердевшего слоя возрастет на dx. По геометрической
сути 
.
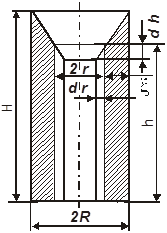
Рис. 75.
Схема формирования усадочной раковины при боковом теплоотводе.
За счет затвердевания элементарного слоя уменьшится объем металла по причине усадки на величину:
, где dVот – элементарный
объем затвердевшего металла, геометрическая форма которого представляет
тонкостенный цилиндр; объем его можно принять:
.
И, следовательно, объем сократившийся в результате усадки составит
.
За счет сокращения объема уровень металла незатвердевшей части отливки понизится на некоторую элементарную высоту dh. Составим уравнение материального баланса усевшего металла, где приравняем увеличение объема усадочной раковины за счет понижения уровня металла объему за счет усадки металла:
.
Преобразуем полученное дифференциальное уравнение и разделим переменные:
.
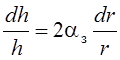Интегрируем левую и правую части дифференциального уравнения:
.
Постоянную интегрирования «с» найдем из начального условия, т.е. при самом начале затвердевания, когда время t = 0, то r = R, а h = H.
.
Решение уравнения приобретает вид:
.
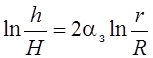После потенциоранирования получаем:
.
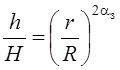Полученная зависимость высоты положения усадочной раковины находится в параболической зависимости от радиуса усадочной раковины и при r = 0, высота раковины h = 0, т.е. основание усадочной раковины достигает дна отливки (рис. 75). В реальных условиях литейной технологии теплоотвод и затвердевание протекает одновременно и в осевом, и в радиальном направлении. Соответственно усадочная раковина в отливке близка к параболической зависимости, но не доходит до дна отливки, а заканчивается в верхней ее части (рис. 76) и hус.р << Но. Это обусловлено тем обстоятельством, что кроме осевого затвердевания отливки снизу вверх за счет теплоотвода в нижнюю часть формы наличие конвекции в расплаве сдвигает усадочную раковину в верхнюю часть отливки. А поскольку усадочная раковина представляет физическую несплошность металла, то при проектировании технологии отливки предусматривают прибыли – увеличенные объемы в верхней части отливки, в которых гарантированно располагается усадочная раковина и не достигает металла отливки (рис. 77).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.