Определение вероятности беспрерывной работы станка. Определение вероятности правильных ответов студентов

значения функции Ф(х)-стандартного нормального распределения даны в статистических таблицах. а) ;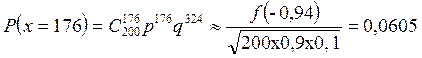

b) ;

c) ;

d) ;

2. Сколько нужно посеять семян, чтобы с вероятностью 0,99 можно было утверждать, что доля взошедших семян среди них отклонится по абсолютной величине от вероятности взойти каждому семени не более, чем на 0,06?

Решение:

Найдем необходимую численность повторной выборки по формуле 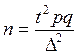, где t – параметр функции Лапласа (Ф(t)=0,99), ∆- абсолютная величина ошибки (отклонение доли взошедших).

Подставим данные: 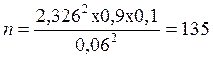 семян.

Задание 4

На пути движения автомобиля четыре светофора, каждый из которых (независимо от других) запрещает дальнейшее движение автомобиля с вероятностью 0,4. Рассматривается случайная величина с.в.  – число светофоров, пройденных автомобилем без остановки.

1.  Составить ряд распределения с.в.  и представить его графически.

2.  Найти функцию распределения с.в.  и построить её график.

3.  Вычислить математическое ожидание (среднее значение) М, дисперсию D и среднее квадратическое (стандартное) отклонение ().

4.  Определить вероятности: а) Р; b) Р; c) Р

Решение:

1.Число пройденных без остановки светофоров случайная величина имеющая распределение  параметрами

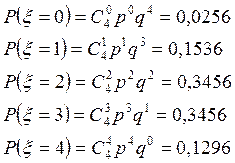
Распишем все возможные значения с.в. ;

k=	0	1	2	3	4	сумма
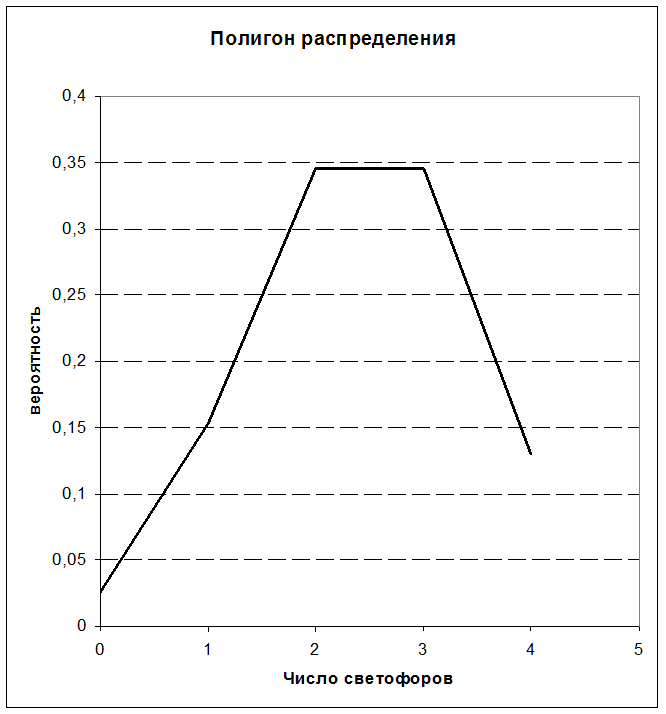
P(ξ=k)	0,1296	0,3456	0,3456	0,1536	0,0256	1

Т.к. сумма всех P(ξ=k) равна 1, то действительно получили ряд распределения.

Для графического изображения ряда отложим по оси абсцисс число пройденных светофоров (k), а по оси ординат соответствующую им вероятность (P(=k)) и соединим полученные точки.

2. Функция распределения с.в.  находится как сумма накопленных вероятностей т.е.  

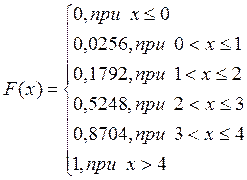
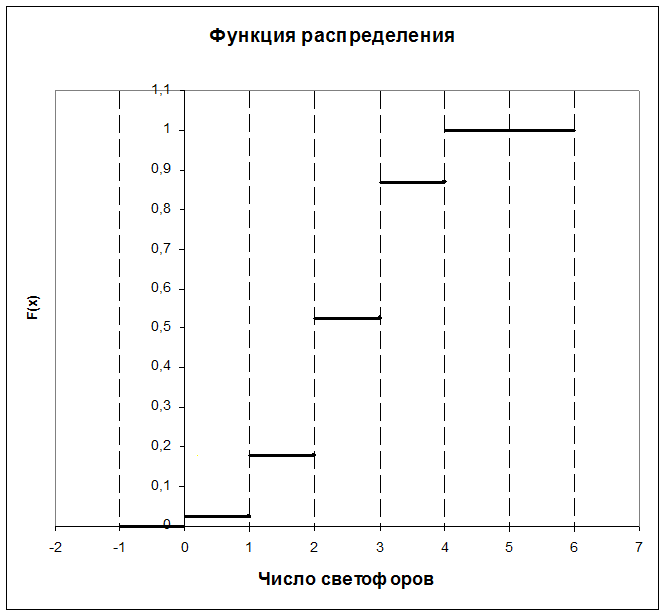
Так же строим график функции распределения.

3. Вычислим математическое ожидание (среднее значение):

, дисперсию D  

среднее квадратическое (стандартное) отклонение

4. Определим вероятности: а) ;

b) ;

c) .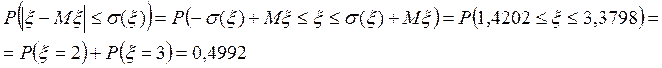

Задание 5

Годовой облагаемый налогом доход  (в тыс. у.е.) наудачу выбранного частного предпринимателя города N является случайным с плотностью распределения

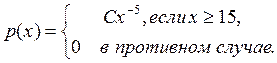
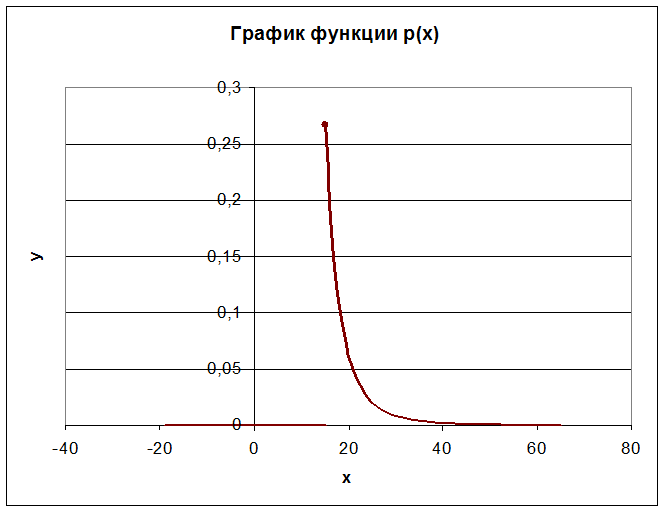
1.  Установить неизвестную постоянную С и построить график функции p(x).

2.  Найти функцию распределения с.в.  и построить её график.

3.  Вычислить математическое ожидание (среднее значение) М, дисперсию D и среднее квадратическое (стандартное) отклонение ().

4.  Во сколько раз число частных предпринимателей города N с доходом, облагаемым налогом меньше среднего, превышает число частных предпринимателей с доходом, облагаемым налогом больше среднего?

Решение:

1. По определению интегральной функции распределения 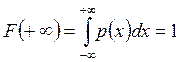 воспользуемся этим свойством:

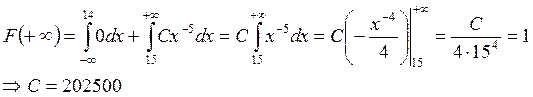
Построим график функции p(x).

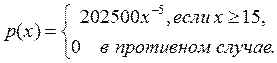
2. Найти функцию распределения с.в.  и построить её график.

Функция распределения:

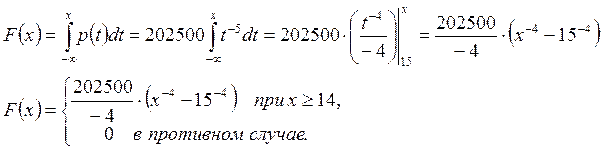
Построим график функции распределения.

3. Вычислим математическое ожидание (среднее значение):

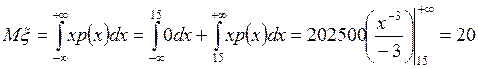, дисперсию D  

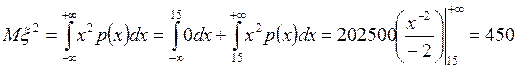
среднее квадратическое (стандартное) отклонение

4Найдем вероятности предпринимателя иметь доход меньше среднего и больше среднего.

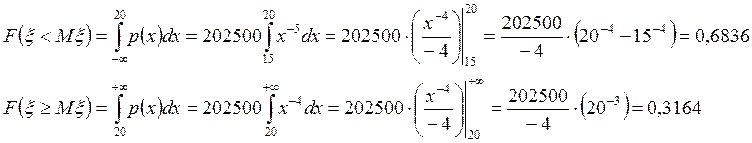 следовательно искомое отношение числа предпринимателей с величиной дохода меньше среднего к числу предпринимателей с величиной дохода больше среднего равно:

Задание 6

При проверке длины 25 деталей изготовленных станком – автоматом были обнаружены следующие отклонения от номинала (в мм):

-0,341	0,291	-0,413	0,849	-0,155	-0,412	-0,125	-0,769	-0,611	0,77
0,605	0,565	-0,167	-0,167	-0,62	-0,072	-0,124	0,085	0,775	-0,132
0,956	0,428	-0,918	1,008	-0,052

Необходимо:

1. Определить исследуемый признак и его тип (дискретный или непрерывный).

2. В зависимости от типа признака построить полигон или гистограмму относительных частот.

3. На основе визуального анализа полигона (гистограммы) сформулировать гипотезу о законе распределения признака.

4. Вычислить выборочные характеристики изучаемого признака: среднее, дисперсию, среднее квадратическое (стандартное) отклонение.

5. Используя критерий согласия «хи-квадрат» Пирсона, проверить соответствие выборочных данных выдвинутому в п.3 закону распределения при уровне значимости 0,05.

6. Для генеральной средней и дисперсии построить доверительные интервалы, соответствующие доверительной вероятности 0,95.

7. С надежностью 0,95 проверить гипотезу о равенстве:

а) генеральной средней значению С;

б) генеральной дисперсии значению 0,25×С ², где C = 1,11.

Решение:

1. Исследуемый признак непрерывный, так как может принимать любые значения на интервале и только точность измерения заставляет их округлять.

2. Ранжируем значения и проведем разбиение на k=1+3,32×lg(25)≈5 интервалов.

Найдем шаг интервала: ;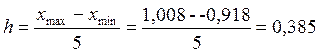

группа по величине отклонения, мм	число деталей	относительная частота
от -0,918 до -0,533	4	0,16
от -0,533 до -0,148	6	0,24
от -0,148 до 0,237	6	0,24
от 0,237 до 0,622	4	0,16
от 0,622 до 1,008	5	0,2
итого	25	1

Построим гистограмму:

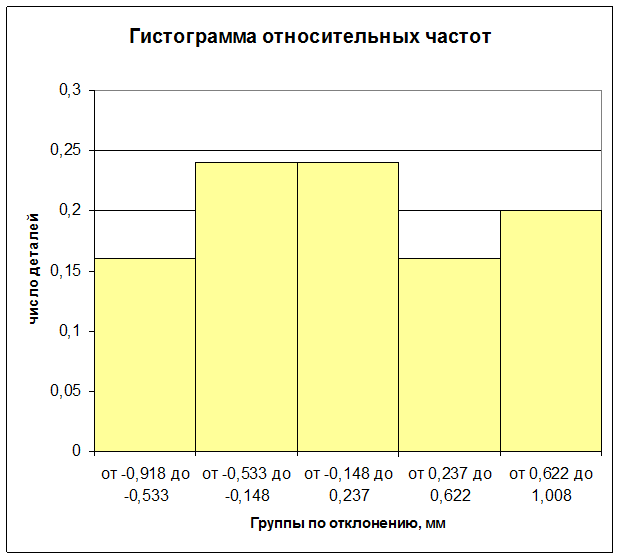
3. При визуальном анализе гистограммы можем выдвинуть гипотезу о том, что признак распределен по нормальному закону.

4. Найдем выборочные характеристики изучаемого признака.

Расчетная таблица:

i	xi	xi2
1	-0,918	0,84272
2	-0,769	0,59136
3	-0,62	0,3844
4	-0,611	0,37332
5	-0,413	0,17057
6	-0,412	0,16974
7	-0,341	0,11628
8	-0,167	0,02789
9	-0,167	0,02789
10	-0,155	0,02403
11	-0,132	0,01742
12	-0,125	0,01563
13	-0,124	0,01538
14	-0,072	0,00518
15	-0,052	0,0027
16	0,085	0,00723
17	0,291	0,08468
18	0,428	0,18318
19	0,565	0,31923
20	0,605	0,36603
21	0,77	0,5929
22	0,775	0,60063
23	0,849	0,7208
24	0,956	0,91394
25	1,008	1,01606
Сумма	1,254	7,58918

Среднее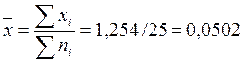

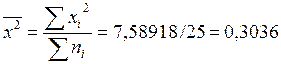
Дисперсия

Среднее квадратическое (стандартное) отклонение

5. Фактическое значение статистики χ² определяется по формуле 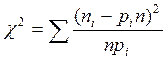, где p_i – теоретическая вероятность попадания случайной величины в i-й интервал 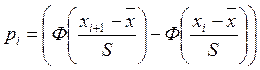, она находится с помощью функции стандартного нормального распределения, значения