Порошковая кристаллография макромолекул, страница 4

Perutz (1954) использовал возмущение параметров решетки у монокристалличнеских данных в первых попытках решить фазовую проблему дискретизацией с повышенной частотой обратного пространства. Этот метод был несомненно нерабочит, из-за развития других более простых фазовых методов. До сих пор мы не пытались использовать отличая в интенсивности, получаемые изз-за изменений элементарной ячейки, не смотря на то, что в теории метод повышения дискретизации обратного пространства может быть применен.

Так же структурная расшифровка может быть улучшена использований подгонки по многим параметрам, с помошью могут быть внесены этого незначительные изменения в структурные факторы. Два независимых исследования hen egg white lysozyme (HEWL) показали, что подгонка по многим параметрам с слабым изменением параметров решетки ведет за собой увеличение полученных интенсивностие и хорошие структурные расшифровки (Bassoetal., 2005; Von Dreele, 2007) с использование модифицированной версии GSAS, которая могла считать малые растяжения пространственной решетки по разным параметрам (Larson & Von Dreele 2004). В нашей лаборатории мы приготовили всего 44 разных HEWL образца при 277 K и комнатной темперетуре и значении pH между 6,56 и 3,33 (Basso etal., 2005). Были собраны высокоразрешенные данные порошковой дифракции при комнатной температуре (λ =1.249826A,ID31,ESRF). Анизотропныя эффект pH на кристаллизацию в тетрагональной пространственной решетку HEWL, здвиг пиков значителен облегчает проблему перекрывания пиков. Для того, чтобы попытаться получить от изучения многих образцов мы выбрали 5 образцов (Картинка 5 с конечной Rietveld расчетом) поперек – изменение pH с использованием расчета Pawley. Рефлексы со значительным отношением сигнал-шум были исследованы визуально и показал максимальное разрешение в 3,2 A.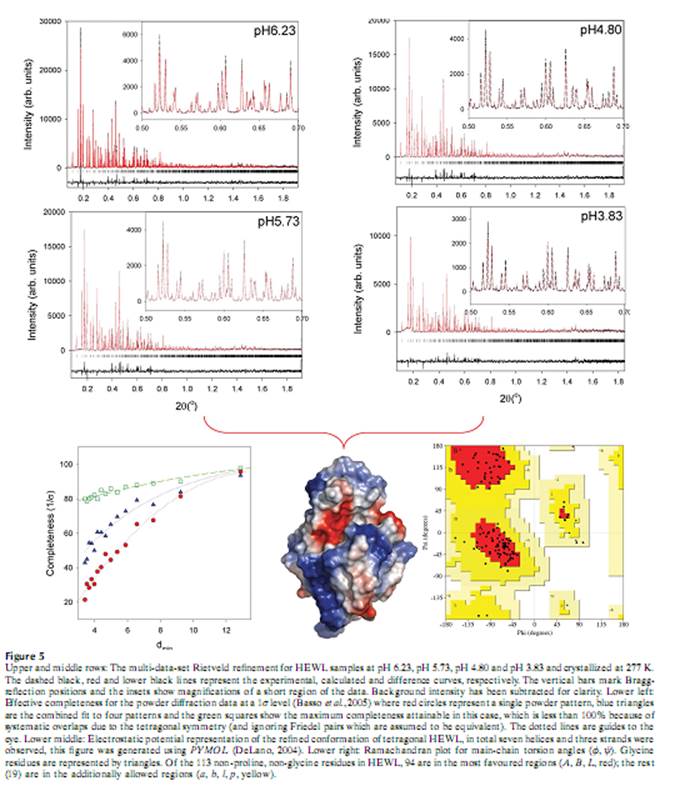

Мы пытались определить предел разрешения этих данных от многих образцов используя методологию, описанную у Sivia (2000). Матрица наименьших квадратов из расчето многих образцов Pawley (1981) характеризовала данные и показала, что характеристическое значение спектральной матрицы связано с ошибкой при извлечении данных интенсивностей (или комбмнации интенсивностей, если пики перекрываются). Для обеспецения легкого сравнения с монокристальной статистикой обработки данных, мы посчитали эффективную полноту для объединенных данных как часть пиков, имеющих отношение I/σ(I) больше, чем порог рис.5 (нижний левый) показывает значительное улечшение эффективной полноты как результат использования объединенные профили для извлечения интенсивностей. Von Dreele (2007) предложил более  легкую схему обсчета, которая так же старается определить улучшения, вызванные использованием данных от многих образцов и может быть применена для обсчета Rietveld.

Такие де четыре гистограммы как те, которые использовались для анализа на полноту были использованы в multi-data-setRietveld обсчете (Rietveld, 1969) для того, чтобы получить среднюю структурную модель для тетрагонального HEWL использую GSAS программное обеспечение (Larson&VonDreele,2004). Некоторые отличия между дифракцией образцов обсчитано с помощью допущением введения коэфициэнта распределения растворителя для того, чтобы отличить для каждой из гистограмм закономерность, что самые большие отличая в интенсивности пиков в основном на малых углах. Более детальное описание этого обсчета можно найти в (Bassoetal., 2005) и модели расположены в pdb database код 2a6u. Верхние картинки на рисунке 5показывают прекрасную подгонку которая может быть достигнута. Мы нашли, что это приближение имело следствием более гладкую и точную расшифровку и выдало структурную модель с прекрасной стереохимией (the resulting Ramachandran plot is shown in the lower right panel of Fig.5)

Von Dreele так же применял пиближение по многим образцам для HEWL но использовал данные с монокристальным разрешени