Исследовать переходные процессы в простейших электрических цепях, содержащих катушки индуктивности, конденсаторы и резисторы

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА ТЕОРЕТИЧЕСКИЕ

ОСНОВЫ ЭЛЕКТРОТЕХНИКИ

ОТЧЕТ

о лабораторной работе №9

«Исследование переходных процессов

в линейных электрических цепях»

Работу выполнил студент группы 3022/1     

           Сморгонский А. В.

Работу принял преподаватель

           Важнов С. А.

Санкт-Петербург, 2005 г.

1.  Цель работы:

Исследовать переходные процессы в простейших электрических цепях, содержащих катушки индуктивности, конденсаторы и резисторы, при подключении их к источнику постоянного напряжения, а также при отключении их от источника.

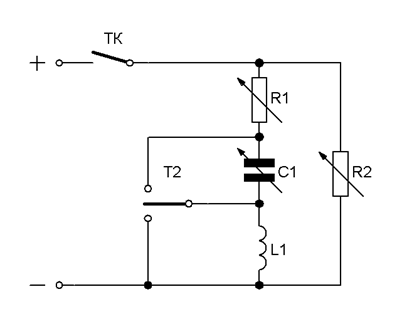
2.  Схема установки:

3.  Программа работы:

3.1  Переходные процессы в цепи с последовательным соединением элементов с R и L.

А) Теоретический расчет.

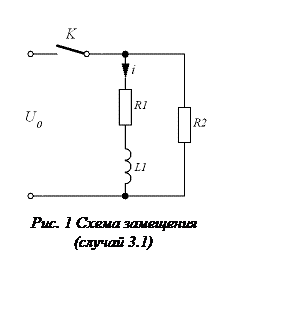Переходный процесс в электрической цепи, изображенной на рис. 1, при подключении к источнику постоянного напряжения описывается следующим уравнением:

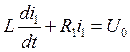
            Решим его:

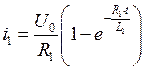
Обозначим через 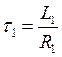постоянную времени цепи и преобразуем полученное выражение:

                                                           

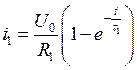
            При отключении от источника постоянного напряжения, переходный процесс в цепи, изображенной на рис. 1 будет описываться следующим уравнением:

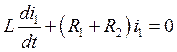
            Его решение:

                                                                                                                          

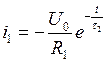
где 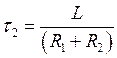 - постоянная времени при выключении цепи.

Б) Экспериментальное исследование.

            В ходе эксперимента были подобраны следующие параметры цепи, при которых характер изучаемых зависимостей выражен наиболее ярко:

R₁ = 1000 Ом, R₂ = 100 Ом, L₁ = 0,235 Гн

            Определим теоретические значения τ₁ и τ₂ используя формулы, полученные в п. 3.1.А:

    

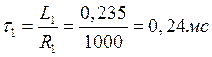
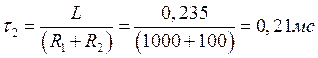
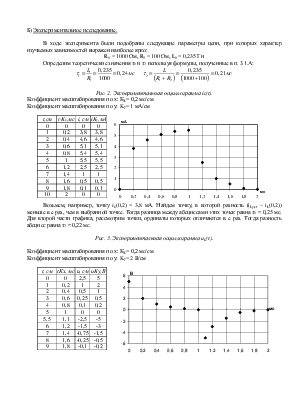
Рис. 2. Экспериментальная осциллограмма i_L(t).

Коэффициент масштабирования по х: К_Х= 0,2 мс/см

Коэффициент масштабирования по у: K_у= 1 мА/см

t,см	t∙Kх,мс	i, см	iKy,мА
0	0	0	0
1	0,2	3,8	3,8
2	0,4	4,6	4,6
3	0,6	5,1	5,1
4	0,8	5,4	5,4
5	1	5,5	5,5
6	1,2	2,5	2,5
7	1,4	1	1
8	1,6	0,5	0,5
9	1,8	0,1	0,1
10	2	0	0

       

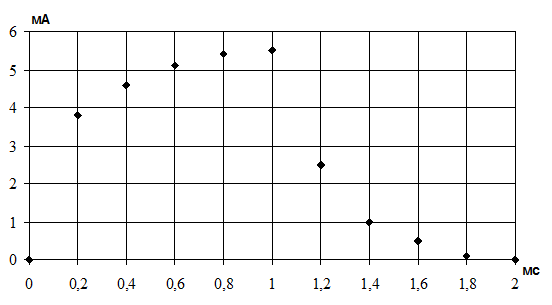
            Возьмем, например, точку i_L(0,2) = 3,8 мА. Найдем точку, в которой разность (i_Lуст – i_L(0,2)) меньше в е раз, чем в выбранной точке. Тогда разница между абсциссами этих точек равна τ₁ ≈ 0,25 мс. Для второй части графика, рассмотрим точки, ординаты которых отличаются в е раз. Тогда разность абсцисс равна τ₂ ≈ 0,22 мс.

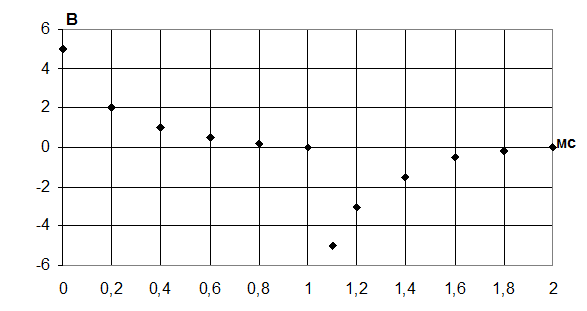
Рис. 3. Экспериментальная осциллограмма u_L(t).

Коэффициент масштабирования по х: К_Х= 0,2 мс/см

Коэффициент масштабирования по у: K_у= 2 B/см

t, см	tKх, мс	u, см	uKy,В
0	0	2,5	5
1	0,2	1	2
2	0,4	0,5	1
3	0,6	0,25	0,5
4	0,8	0,1	0,2
5	1	0	0
5,5	1,1	-2,5	-5
6	1,2	-1,5	-3
7	1,4	-0,75	-1,5
8	1,6	-0,25	-0,5
9	1,8	-0,1	-0,2

3.2  Переходные процессы в цепи с последовательным соединением элементов с R и С.

А) Теоретический расчет.

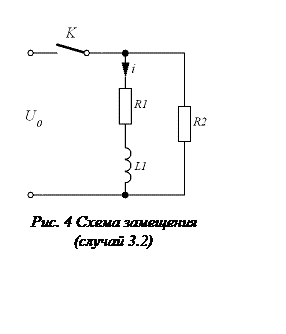Переходный процесс в электрической цепи, изображенной на рис. 4, при подключении к источнику постоянного напряжения описывается следующим уравнением:

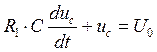
            Решим его:

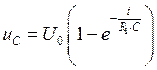
Обозначим через постоянную времени цепи и преобразуем полученное выражение:

                                                           

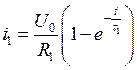
            При отключении от источника постоянного напряжения,

переходный процесс в цепи, изображенной на рис. 4 будет описываться следующим уравнением:

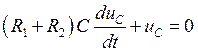
            Его решение:

                                                                                                                            

где  - постоянная времени при выключении цепи.

Б) Экспериментальное исследование.

            В ходе эксперимента были подобраны следующие параметры цепи, при которых характер изучаемых зависимостей выражен наиболее ярко:

R₁ = 1000 Ом, R₂ = 100 Ом, С = 0,2 мкФ

            Определим теоретические значения τ₁ и τ₂ используя формулы, полученные в п. 3.1.А:

Рис. 5. Экспериментальная осциллограмма i_С(t).

Коэффициент масштабирования по х: К_Х= 0,1 мс/см

Коэффициент масштабирования по у: K_у= 2 мА/см

t, см	t∙Kх, мс	i, см,	i∙Ky,мА
0	0	2,25	4,5
1	0,1	1,25	2,5
2	0,2	0,75	1,5
3	0,3	0,25	0,5
4	0,4	0,1	0,2
5	0,5	0	0
5,5	0,55	-2,25	-4,5
6	0,6	-1,75	-3,5
7	0,7	-1	-2
8	0,8	-0,75	-1,5
9	0,9	-0,25	-0,5

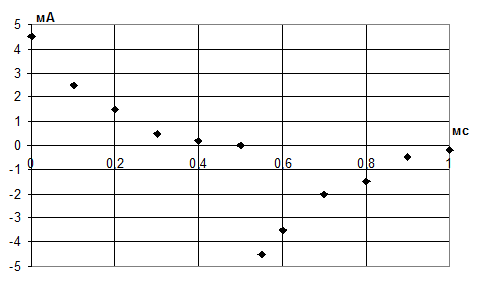
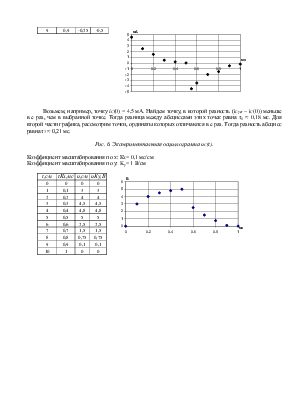
            Возьмем, например, точку i_С(0) = 4,5 мА. Найдем точку, в которой разность (i_Суст – i_С(0)) меньше в е раз, чем в выбранной точке. Тогда разница между абсциссами этих точек равна τ₁ ≈ 0,18 мс. Для второй части графика, рассмотрим точки, ординаты которых отличаются в е раз. Тогда разность абсцисс равна τ₂ ≈ 0,21 мс.

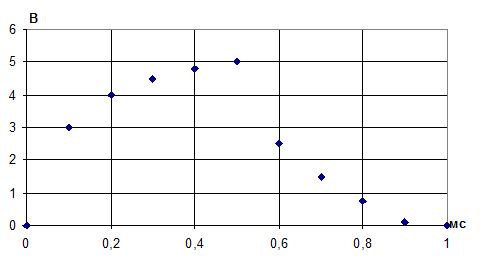
Рис. 6. Экспериментальная осциллограмма u_С(t).

Коэффициент масштабирования по х: К_Х= 0,1 мс/см

Коэффициент масштабирования по у: K_у= 1 B/см

t,см	tKх,мс	u,см	uKy,В
0	0	0	0
1	0,1	3	3
2	0,2	4	4
3	0,3	4,5	4,5
4	0,4	4,8	4,8
5	0,5	5	5
6	0,6	2,5	2,5
7	0,7	1,5	1,5
8	0,8	0,75	0,75
9	0,9	0,1	0,1
10	1	0	0

3.3  Переходные процессы в цепи с последовательным соединением элементов с R, L  и С.

А) Теоретический расчет.

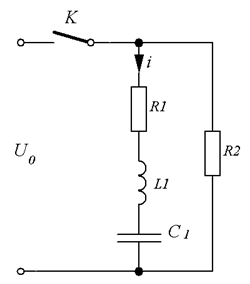Переходный процесс в электрической цепи, изображенной на рис. 7, при подключении к источнику постоянного напряжения описывается следующим уравнением:

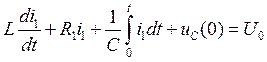
            При нулевых начальных условиях, т.е. при

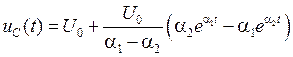
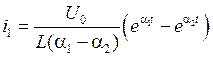
где  - корни характеристического уравнения, .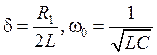

            Характер переходного процесса зависит от соотношения между параметрами R, L, C. При δ > ω₀, корни α₁ и α₂ – вещественные и переходный процесс апериодический. Если же δ < ω₀, корни α₁ и α₂ –комплексные и получаем затухающие колебания тока и напряжения на конденсаторе.

            При размыкании ключа, процессы в этой цепи описываются следующими соотношениями:

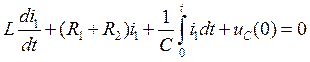
Если принять u_C(0) = U₀, то

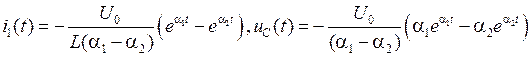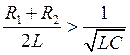
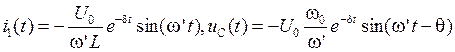 при

 при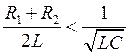

Так как при разрядке конденсатора 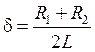, то корни характеристического уравнения, а также угловая частота ω’ колебаний и начальная фаза θ напряжения на конденсаторе будут отличаться от найденных выше.

            Однако, если δ >> ω₀, то для корней можем написать приближенные выражения:

  

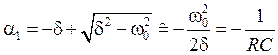
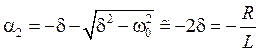
Вместо R здесь следует написать R₁ или R₁+R₂ соответственно при заряде или разряде конденсатора.

Б) Экспериментальное исследование.

            В ходе эксперимента были подобраны следующие параметры цепи, при которых характер изучаемых зависимостей выражен наиболее ярко:

R₁ = 50 Ом, R₂ = 20 Ом, С = 0,4 мкФ, L = 46 мГн

            Определим теоретические значения δ и ω₀:

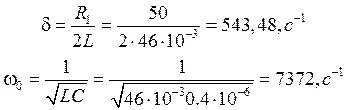
            1) Затухающий колебательный процесс.

            Теперь проверим условие возникновения затухающих колебаний. Видим, что δ < ω₀, т.е. условие выполняется.

Рис. 8. Экспериментальная осциллограмма i_С(t).

 

Рис. 9. Экспериментальная осциллограмма u_С(t).

            Определим значения δ и ω₀ из графиков. Для этого возьмем две соседние точки, в которых функция обращается в ноль. Разница абсцисс этих точек есть период этих колебаний. Тогда ω₀:

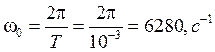
            Декремент затухания есть величина, обратная времени, в течение которого, амплитуда колебаний уменьшается в е раз.

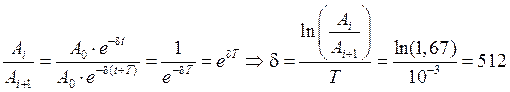
2) Апериодический процесс.

R₁’ = 5000 Ом

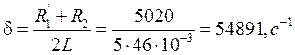
            Проверим условие возникновения апериодических колебаний. Видим, что δ > ω₀, т.е. условие выполняется.

Рис. 10. Экспериментальная осциллограмма i_С(t).

Рис. 11. Экспериментальная осциллограмма u_С(t).