2. Область значений - вся числовая ось
3. При a>1 функция строго возрастает при 0<a<1 функция строго убывает
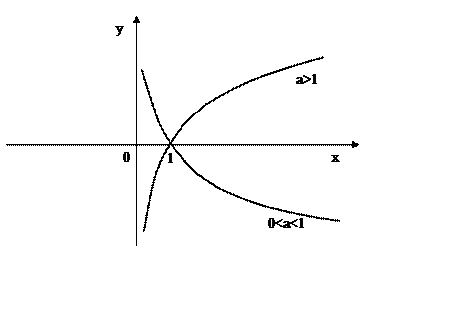
Рис. 1.4
г) Тригонометрические функции y=sin(x), y=cos(x) Свойства для функции y=sin(x)
1. Область определения вся числовая ось
2. Область значений [-1,+1]. Функция ограничена |sin(x)|<1
3. Функция y=sin(x) нечетная функция: sin(-x)= - sin(x)
4. Функция y=sin(x) периодическая с основным периодом 2π sin(x+2π)=sin(x). Для y=cos(x) все то же, только эта функция четная cos(-x)=cos(x)
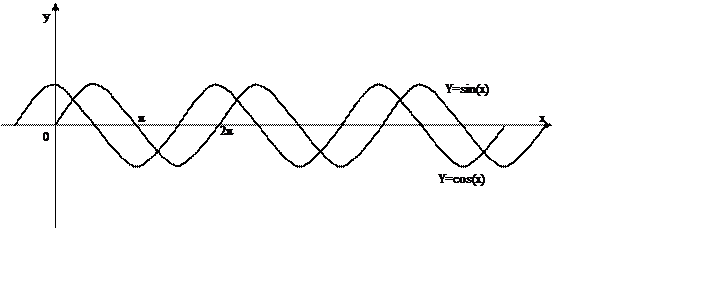
Рис. 1.5
д) Натуральный логарифм y=ln(x)
Десятичный логарифм y=lg(x)
Связь:
ln(x)=2,303∙lg(x)
lg(x)=0,4343∙ln(x)
e) Экспоненциальная функция
y=ex обратная функции y=ln(x) называется экспоненциальной
1.3. Предел функции
Пусть функция f (х) определена в некотором интервале (х0 - h; x0 + h), h> 0, за исключением, быть может, точки х0. В этой точке х0 для функции f(х) возможны только следующие случаи: 1) непрерывность, 2) разрыв, 3) функция не определена в точке х0. Однако бывает так, что в двух последних случаях функции f(х) можно приписать в точке х0 такое значение А, что она станет непрерывной в точке х0. Это называется доопределить функцию f(х) по непрерывности в точке x0, а число А называется тогда пределом функции f(х) при x, стремящемся к х0.
Определение
1. Число А
называется пределом функции f(х)
при х, стремящемся к х0 (х→х0), если функция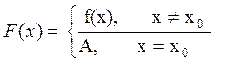 
непрерывна в точке х0. Коротко (символически) это записывают так:
Например, если функция f(х) непрерывна в точке х0, то, взяв A = f(x0), мы получим, что F(x) = f(x), и, следовательно, для любой непрерывной в точке х0 функции справедливо равенство
и обратно.
Какие
наглядные представления полезно связать с пределом функции? Непрерывность
функции F(х) в точке х0 означает,
что F(х) ≈ F(х0) для всех х, близких к х0, и
точность этого равенства можно сделать как угодно большой за счет приближения х
к х0. Если это переписать в терминах функции f(х), то получим: равенство 
означает, что f(х) ≈ А для всех х ≠ х0 и
близких к х0 (при х = х0 функция f(х) может быть не определена, а для х ≠ х0 F(x) = f(x); F(x0) = A) и точность этого равенства можно сделать как угодно
большой за счет приближения х к х0.
Теорема 5. Если существуют 
и 
, то
1) 
2) 
3) 
4) 
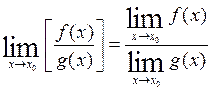, если 
Следующие теоремы рассмотрим без доказательства.
Теорема 1. Если существует
, а функция f(t) непрерывна
в точке t0, то
Коротко говорят: знак предела и знак непрерывной функции можно менять местами.
Теорема
2 (замена
переменной). Если существуют 
и 
, а g(x)≠t0 при x≠x0, то выполняется равенство 
Теорема 3 (единственность предела).
При x→х0 функция f (х) не может иметь двух пределов.
Теорема 4 (о промежуточной функции).
Если f(x)≤p(x)≤g(x) при всех х≠x0 и
, то 
Теорема
5. Пусть . Если f(x)≥0, то А≥0. Если
f(x)≤0, то А≤0.
Теорема 6. (переход к пределу в неравенствах). Если f (x)≤g(x), то
(если эти пределы существуют).
Определение 2. Функция α(х) называется бесконечно малой при х→x0, если
Бесконечно малые функции обычно обозначают греческими буквами а(х), β(х), . . . или, опуская аргумент, α, β.
Теорема
7. Для равенства необходимо и достаточно,
чтобы функция α(x) = f(x)-A была бесконечно малой при х→x0.
1.4. Замечательные пределы:
Первый замечательный
предел: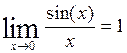 
Для доказательства
возьмем сектор ОАС окружности радиуса 1 (Рис. 1.6) с центральным углом, равным x (радиан), 0<x<π/2, и проведем 
. Тогда площадь
треугольников и сектора будут связаны соотношением:
пл. ∆ОАС < пл. сект. ОАС < пл. ∆ОВС
или
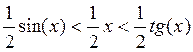
Рис. 1.6
Разделив
все части этого неравенства на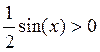 
, получим
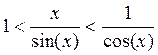или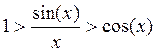 
Это неравенство, доказанное для любых х из интервала (0; π/2), верно для любого х≠0 из интервала (- π/2; π/2) в силу четности функций, входящих в это неравенство.
Второй замечательный предел имеет две формы записи:
1) 
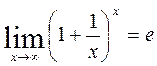2) 
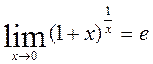
Это выражение мы доказывать не будем, доказательство довольно сложное. Предел обозначается буквой е в честь открывшего его петербургского математика Леонарда Эйлера. Это иррациональное число: е=2,718281828459… (обычно в расчетах используют е≈2,7).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.