2) Аналитический способ
Это способ задания функций с помощью формул. Он компактен, легко воспроизводим и, главное, наиболее приспособлен к выполнению математических действий - арифметических (сложение, умножение), действий высшей математики (дифференцирование, интегрирование). Но он не всегда нагляден.
Аналитический способ задания функции состоит в том, что соответствие между x и y задается при помощи формулы.
а) в явном виде: y2=r2 – x2
б) в неявном виде: f(x,y)=0; x2 + y2 – r2=0
Достоинства аналитического способа задания функции – понятна область определения, точные значения функции можно вычислить, работать с функцией несложно. Недостаток аналитического способа задания функции – его малая наглядность, т.е. трудно получить ответы на вопросы как ведет себя функция на некотором интервале, особенно если формула сложна.
3) Параметрический способ
когда X и Y выражаются через вспомогательные параметры:
x=Rcos(x)
y=Rsin(x)
x2+y2=R2
4) Графический способ
Сначала определим понятие графика функции.
Определение: Графиком функции y=f(x) называется множество точек на плоскости с координатами (x; f(x)), где x – любое число из области определения функции.
|
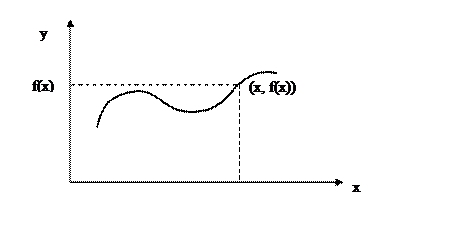
Рис. 1
График представляет собой линию (Рис. 1) состоящую из одного или нескольких кусков. Например, графиком функции y=kx+b служит прямая линия (график состоит из одного куска), а графиком функции y=1/x служит гипербола (линия состоит из двух кусков). График функции есть такая линия, координаты любой точки которой связаны соотношением y=f(x). Задать функцию графически значит нарисовать ее график. Это делают все самопишущие приборы – они вычерчивают графики изучаемых функций. Графическое задание функции чрезвычайно наглядно, по графику видно как меняется функция, когда она возрастает, а когда убывает. Однако в точности графическое представление функции проигрывает. Из чертежа можно получить любое значение функции, измерив ординату соответствующей точки графика. Это измерение можно сделать только с некоторой ошибкой, зависящей от чертежа и измерительных приборов, – это недостаток способа. Удобнее всего изучать функцию, заданную и аналитически, и графически.
Основные характеристики функции.
1) Областью определения функции называют совокупность всех значений аргумента х, для которых функция y=f(x) определена. Обозначают D(f).
2) Совокупность всех возможных значений y называют областью значений функции и обозначают E(f).
3) Возрастающие и убывающие функции.
Функция называется возрастающей если: Δx>0, Δy>0; Δx<0, Δy<0.
Функция называется убывающей если: Δx>0, Δy<0; Δx<0, Δy>0.
4) Периодичность функции.
Функция называется периодической если выполняется равенство f(x)=f(x+T), где Т называется периодом функции.
5) Четность и нечетность функции.
Функция называется четной если выполняется равенство: f(-x)=f(x)
Функция называется нечетной если выполняется равенство: f(-x)=-f(x)
6) Экстремум функции.
Если функция y=f(x) имеет экстремум в точке х=а, тогда если выполняется условие f(a)>f(x), то в этой точке будет максимум функции.
Если функция y=f(x) имеет экстремум в точке х=а, тогда если выполняется условие f(a)<f(x), то в этой точке будет минимум функции.
7) Обратная функция.
Функция f называется обратной, если обратное ей соответствие – функция.
y=f(x) и x=φ(y).
Чтобы для функции f(x), заданной формулой, найти ей обратную, нужно в формуле
поменятьx на y иy на x
и разрешить уравнение относительно y. Пример: y=x2 обратная x=y2 или y=
.
1.2. Графики основных элементарных функций.
a) Степенная функция y=xn
Область определения зависит от
показателя степени n: для n
0 областью определения служит вся
числовая ось, для n<0 – вся
числовая ось за исключением точки х=0.
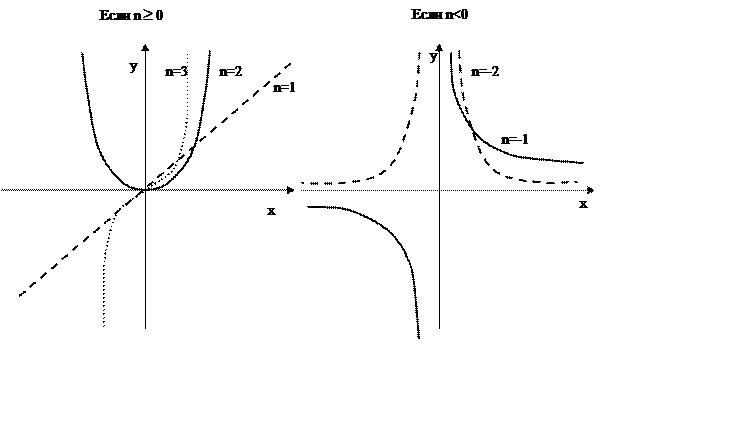
Рис. 1.2
б) Показательная функция y=ax
(a>0 и a≠1)
1. Область определения вся числовая ось.
2. Область значений - только положительные значения.
3. Если а>1
показательная функция строго возрастает если 0<a<1 показательная функция
строго убывает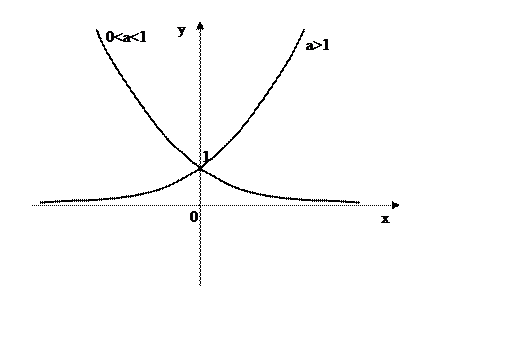 
Рис. 1.3
в) Логарифмическая функция y=loga (x) обратная показательной функции
Свойства:
1. Область определения - положительные числа
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.