Производная функции. Пример задачи приводящей к понятию производной. Физический смысл производной, страница 3

Рис. 2.5

Таким образом, средняя скорость не может отразить особенностей движения тела и дать представление об истинной скорости его движения в момент времени t. Однако по мере уменьшения промежутка времени ∆t средняя скорость движения тела будет характеризовать движение более полно. При ∆t→0 средняя скорость стремится к своему пределу, представляющему скорость движения тела в данный момент времени, или мгновенную скорость. Поэтому

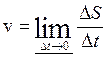.  Мгновенная скорость есть предел отношения приращения пути к приращению времени, когда приращение времени стремится к нулю.

Отвлекаясь от конкретного содержания каждой задачи, результат соответствующих математических вычислений называют Производной. Рассмотрим понятие производной и на примере некоторых задач покажем, как оно возникает и как при помощи производной и родственных понятий решаются задачи.

2.3. Производная функции

Производной функции   y = f(x) в точке х₀ называется предел отношения приращения функции к приращению аргумента при стремлении этого приращения к нулю:

.

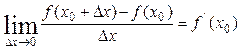Очень удобна более короткая запись для этого предела и более короткое обозначение для производной  .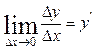

Примеры.

1. y = f(x)=x², тогда

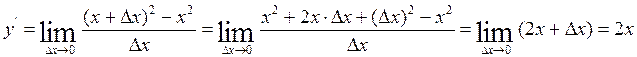
Коротко полученный результат записывается так: (х²)' = 2х.

2. (С)' =0 (С — постоянная):

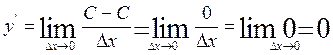
2.4. Физический смысл производной:

Производная функции y=f(x) по аргументу х есть мгновенная скорость изменения функции y=f(x).

Путь, который проходит точка, зависит от времени t, т.е. путь s есть функция от времени t: s=s(t). Чтобы вычислить скорость точки v, надо взять два ее положения в моменты времени t и t+Δt. Тогда v=Δs/Δt, причем это равенство тем точнее, чем короче промежуток времени Δt.  В пределе же, при Δt→0,  получим точное равенство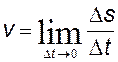 

Аналогично можно рассмотреть определение ускорения а. Производная от скорости по времени есть ускорение.

Пусть точка М движется по прямой. Путь s, который проходит эта точка, зависит от времени t,  т.e. путь s есть функция от времени t: s=s(t). Чтобы вычислить скорость v точки, надо взять два ее положения М и М₁  в моменты времени t и t + ∆t. Тогда , причем, это равенство тем точнее, чем короче промежуток времени ∆t. В пределе же, при ∆t→0, получим точное равенство

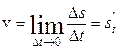
Чтобы подсчитать ускорение а, надо подсчитать изменение скорости v за единицу времени. Сама скорость v есть функция времени: v=v(t). За промежуток времени от t до t + ∆t скорость изменилась на величину ∆v=v(t+∆t)-v(t)  и потому . Так же как и при вычислении скорости, это равенство переходит в точное, если перейти к пределу при ∆t→0:

.

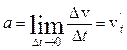Производная - это скорость изменения функции. Из определения производной  следует: 

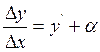, где α - бесконечно малая при ∆х→0. Отбросив α, получим приближенное равенство 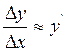, из которого видно, что у' есть коэффициент пропорциональности между ∆y и ∆x. Если у' = 2, то ∆y в 2 раза больше ∆x; если у' = 0,1, то ∆y в 10 раз меньше ∆x(больше в 0,1 раза); если у' = - 3, то ∆y имеет знак, противоположный знаку ∆x, и по модулю в 3 раза больше (т. е. с увеличением ∆xуменьшается ∆y). Это и имеется в виду, когда говорят, что производная - это скорость изменения функции.

2.5. Геометрический смысл  производной: