Специализация перегрузочных комплексов, страница 3

,     γ = 1, 2, …, c;            (11.7)

4) знак аргумента X_ijγ ≥ a.

Необходимо найти значение (X_ijγ), минимизирующее целевую функцию.

Для оптимизации решения задачи специализации причалов и складов порта можно использовать специальный математический метод, а именно:

симплекс-метод с выполнением расчетов на ЭВМ по стандартной программе.

Вместе с тем, учитывая степень точности исходной информации, допускается применение упрощенного метода, позволяющего найти оптимальное или близкое к оптимальному решение с меньшей трудоемкостью. В основу данного метода положен метод разрешающих множителей Л. В. Канторовича с трактовкой применительно к задаче специализации причалов и складов порта.

Идею метода удобно пояснить на цифровом примере.

Условие задачи. В течение навигации порт должен освоить четыре грузопотока с разной характеристикой на трех  взаимозаменяемых  причалах. Оборудование причалов неодинаково, но условия складирования идентичны и не ограничивают возможности причалов.

Необходимо распределить грузопотоки по причалам так, чтобы минимизировать комплексные расходы по порту и флоту на их освоение. Исходные данные сведены в табл. 11.2. В клетках структурной части этой таблицы на пересечении линии i-гo грузопотока и j-го причала записаны сверху удельный бюджет времени причала τ_ij , (ч/т), снизу удельные комплексные расходы S_ij , (р./т), затрачиваемые на тонну грузопотока.

По всем причалам плановый бюджет времени T_j = 4900 ч.

Порядок распределения грузопотоков предусматривает первоочередное использование причалов, следование груза через которые связано с минимальными комплексными расходами. Но ввиду различия трудоемкости грузов комплексные расходы по их освоению в натуральном виде (табл. 11.2) несопоставимы. Требуется выразить их в соизмеримых величинах с помощью условных оценок, которые назовем разрешающими множителями.

Система условных оценок состоит из двух групп: оценки трудоемкости и условных расходов.

Оценка трудоемкости ε_i, учитывающая сравнительные затраты средств на освоение разных грузопотоков по причалам, определяется из выражения

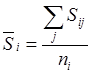 ;      ,       (11.8)

где А — любое число. Удобно принять А = _max.

Условные расходы по i-му грузопотоку при следовании через j-и причал S_ij΄ определяются по формуле

.             (11.9)

В цифровом выражении:

по первому грузопотоку

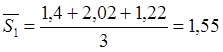
аналогично   .

Наибольшее среднее значение условных расходов у третьего грузопотока .

Тогда ;  аналогично ε₂ = 1,66; ε₃ = 1; ε₄ = 2;

Условные расходы по первому грузопотоку при следовании его через первый причал составят    ; .

Преобразованные таким образом исходные данные заносим в рабочую матрицу (табл. 11.3). Она строится на базе табл. 11.2 с добавлением столбца значении ε_i, и двух строк: нижней с величиной планового бюджета времени причала Т_j  и строки над ней, учитывающей неиспользованный  бюджет времени причала (резерв). Кроме того, в структурной части табл. 11.3 в клетках значение удельных комплексных расходов заменяются соответствующей величиной условных расходов S_ij΄.

Таблица 11.2