Определение средней урожайности зерновых с/х предприятий. Расчет сводных индексов цен, физического объема реализации и товарооборота

Задача 1. На основании следующих данных по двум с/х предприятиям определите насколько и в каком из них средняя урожайность зерновых выше.

Культура	Предприятие 1		Предприятие 2
	Валовой сбор, ц	Урожайность, ц/га	Посевная площадь, га	Урожайность, ц/га
	xf	x	f	x
Пшеница	32000	26	1580	20
Рожь	1600	19	130	19
Ячмень	13750	20	660	18
Просо	1750	13	120	13
Итого	49100	-	2490	-

Найдем среднюю урожайность по каждому предприятию с применением средней арифметической взвешенной. Взвешенная средняя учитывает различное значение отдельных вариантов в пределах совокупности и применяется, когда варианты имеют различную численность.

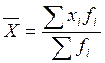
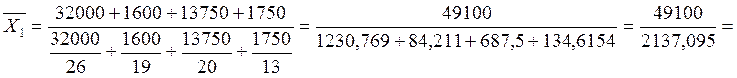
 ц/га

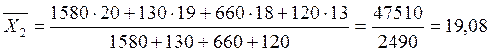ц/га

 ц/га

Таким образом, на предприятии 1 средняя урожайность зерновых выше на 3,895 ц/га.

Задача 2.

По данным таблицы найдите:

·  Моду и медиану, используя частоты и частости;

·  Дисперсию и среднее квадратичное отклонение, коэффициент вариации.

Размер Прибыли млрд.руб.	3,7-4,6	4,6-5,5	5,5-6,4	6,4-7,3	7,3-8,1	Итого
Число банков	2	5	9	4	2	22

Решение

Мода – это чаще всего встречающийся вариант.

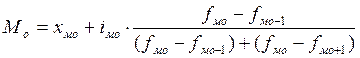, где     х_мо – нижняя граница модального интервала,

i_мо – величина модального интервала,

f_мо,f_мо-1,f_мо+1 – частота модального, домодального и послемодального интервала

Медианой в статистике называется вариант, делящий численность упорядоченного вариационного ряда на две равные части. Медиана ряда наблюдений может быть очень далека от типичной величины. Медиана имеет особое свойство – сумма отклонений членов ряда от медианы есть величина наименьшая.

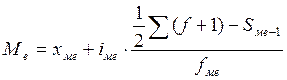, где     х_ме – нижняя граница медианного интервала,

i_мо – величина медианного интервала,

S_ме-1 – сумма накопленных частот в домодальном интервале.

Для удобства часть вычислений занесём в таблицу:

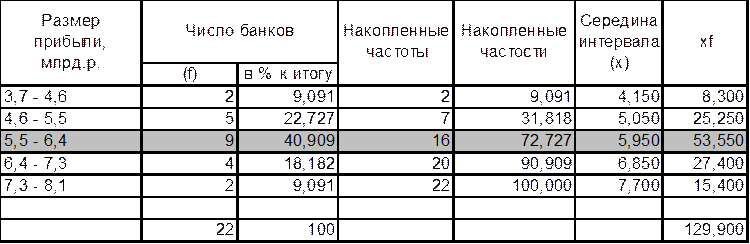
Сначала вычислим моду и медиану через частоты:

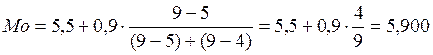 млрд.руб.,

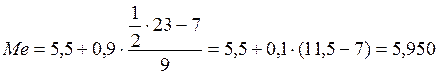   млрд.руб.

Теперь вычислим значения моды и медианы через частости:

 

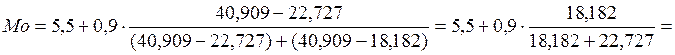
млрд.руб.,

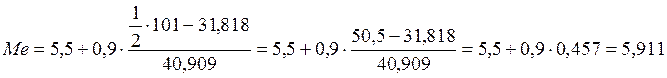 млрд.руб.

Вычислим среднее арифметическое взвешенное:

,

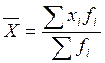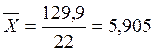 млрд.руб.

5,911	>	5,905	>	5,900
Ме				Мо

Можно сказать, что средняя арифметическая взвешенная, медиана и мода практически совпадают. В этом случае говорят, что данная группа симметрична.

Вариация – это различие в значениях какого-либо признака у разных единиц одной совокупности в один и тот же период или момент времени. Степень колеблемости отдельных значений признака от средней отражают следующие обобщающие показатели: дисперсия, среднее квадратическое отклонение и коэффициент вариации.

Дисперсия – средняя арифметическая квадратов отклонений отдельных значений признака от их средней арифметической.

.

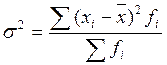Среднее квадратическое отклонение () – корень квадратный из дисперсии. Это абсолютная мера вариации признака в совокупности.

Для сравнения величины вариации различных признаков и также для сравнения степени вариации одноименных признаков в нескольких совокупностях исчисляется относительный показатель вариации – коэффициент вариации. По величине этого коэффициента можно судить о степени вариации признаков. Чем больше величина коэффициента вариации, тем больше разброс значений признака вокруг средней, и тем исследуемая совокупность по своему составу менее однородна.

.

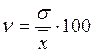Опять занесем часть вычислений в таблицу:

, 

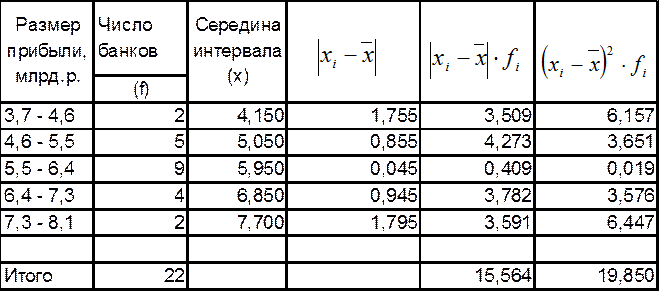
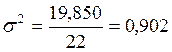 млрд.руб,

.

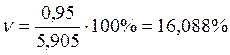16,088 % < 30 % , значит совокупность однородна.

Ответ: Мо = 5,9 млрд.руб., Ме = 5,911 млрд.руб., = 0,902,

            = 0,95 млрд.руб., = 16,088%.

Задача 3.

По данным таблицы рассчитайте сводные индексы цен, физического объема реализации и товарооборота, а также величину перерасхода покупателей от роста цен.

Решение.

Занесем часть промежуточных вычислений в таблицу:

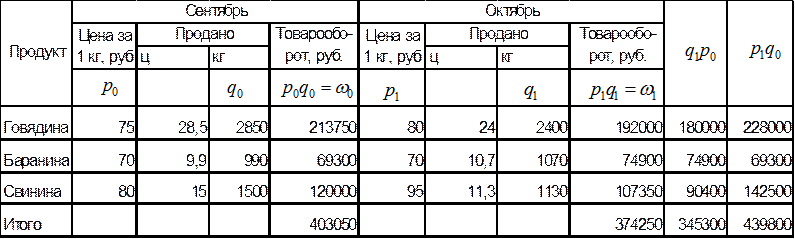
Рассчитаем сводные индексы по двум видам формул:

1.  По формулам Ласпейреса.

Индекс физического объема	Индекс цены

2.  По формулам Паше.

Индекс физического объема	Индекс цены

Теперь найдем индекс товарооборота:

, 

или

, .

Таким образом, произошло уменьшение товарооборота на 7,1%  в связи с увеличением цены на 8,4 % и уменьшением физического объема реализации на 14,9%. Показатели ухудшились из-за уменьшения физического объема реализации. Найдем величину перерасхода покупателей от роста цен.

,

млрд.руб.

Ответ: сводный индекс цен – 1,084, сводный индекс физического объема реализации – 0,851, сводный индекс товарооборота – 0,929, величина перерасхода покупателей от роста цен – 28950 млрд. руб.

Задача 4

Имеются следующие данные о производстве электроэнергии в регионе за 1996-2000 гг. (млрд. кВт/ч):

Для анализа ряда динамики определите:

1.  цепные и базисные:

·  абсолютные приросты;

·  темпы роста;

·  темпы прироста;

2.  абсолютное значение прироста;

3.  средний уровень ряда, среднегодовой абсолютный прирост, среднегодовой темп роста, среднегодовой темп прироста.

Решение.

Ряд динамики представляет собой ряд расположенных в хронологической последовательности числовых значений показателя, показывающих изменение явлений во времени.

Для анализа рядов динамики применяются следующие показатели: абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процента прироста.

Показатели ряда динамики могут вычисляться как на постоянной, так и на переменной базах сравнения. Сравниваемый уровень называется отчетным, а уровень, с которым производится сравнение – базисным. При расчете показателей ряда динамики на постоянной базе сравнения в качестве