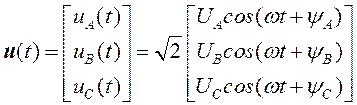Энергетические компоненты трехфазного тока, их оплата и компенсация, страница 2

Синусоидальный режим с уравновешенным током. В синусоидальном  режиме в точке присоединения к сети с синусоидальным (несимметричным) напряжением

                                  (15) в трёхпроводном сечении  протекают синусоидальные токи

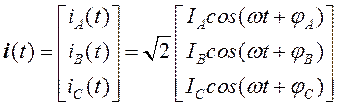.                                 (16)

Синусоидальные напряжения и токи однозначно определены трёхмерными векторами с комплексными действующими величинами (3D-комплексами):

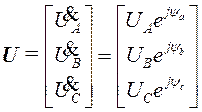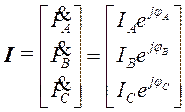,        .                    (17)

3D-комплексы позволяют компактно записать векторы мгновенных значений напряжения и тока:

,       .                                  (18)

При этом действующие величины тока  и напряжения можно вычислить, не используя интегралы (7) и (10):

 ,                   (19)

Для трёхпроводного сечения  эквивалентные проводимости фаз определяются [5] как

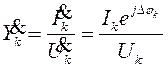
                                      (20)

где  – разность фаз между током и напряжением в k-фазе.

Если в сечении  подключена нагрузка типа звезды с заземлённой нейтралью, то введённые проводимости (20) равны проводимостям фаз нагрузки. Если эквивалентные проводимости (20) во всех фазах одинаковы:

 ,                     (21)

то ток сбалансирован с напряжением (уравновешен) [3]. В уравновешенном режиме для мгновенных трёхфазных величин тока справедливо выражение:

   .                                            (22)

Величина  и имеет размерность проводимости, а  – общий фазовый сдвиг между трёхфазными токами и напряжениями.

Комплексная проводимость

                                     (23а) 

                                (23б)

определяет комплексную мощность

.                                  (24)

Вещественная часть комплексной мощности (24) равна средней (активной) мощности

;                                               (25)

мнимая часть – определяет  реактивную мощность

 .                                              (26)

Активная мощность (активная проводимость) положительна – нагрузка потребляет энергию. Реактивная мощность (реактивная проводимость) как положительна, так отрицательна. Функция знака величины

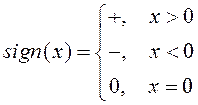                                         (27)

позволяет учесть смену "направления поступления" реактивной мощности (от потребителя к поставщику).

Положительная реактивная мощность, или отрицательная реактивная (индуктивная) проводимость интерпретируется как потребление электроэнергии. Отрицательная реактивная мощность или положительная емкостная проводимость интерпретируется как отдача (генерация) электроэнергии

 ,                            .

Уравновешенный ток (22) представляется суммой двух составляющих:

 .                         (28)

Первая компонента (синфазная с напряжением) определяет активный ток Fryze [7]:

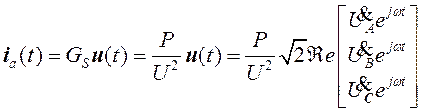 ,                         (29)

вторая компонента сдвинута на четверть периода () и определяет реактивный ток

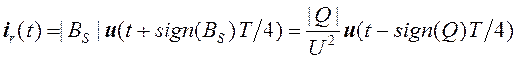.              (30)

3D-комплексы этих токов равны соответственно:

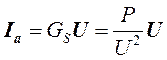 ,                                             (31)

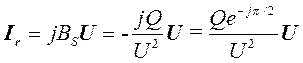.                        (32)

Действующие величины активного и реактивного токов записывают как

 ,                                                     (33)

.                                                    (34)

Для активной и реактивной мощности выполнены условия

 ,                  (35)

 ;                    (36)

модуль комплексной мощности (геометрическая полная мощность [8]):

,                    (37)

и полная мощность (9) равны (соответственно: не надо имеется ввиду, что эти мощности равны друг другу)

    и       .                   (38)

Уравнение нормированных потерь (на один Ом) для уравновешенного режима в точке подключения записывается как

  .                            (39)