

























МІНІСТЕРСТВО ОСВІТИ ТА НАУКИ УКРАЇНИ
НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ
«ХАРКІВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ»
Кафедра автоматизації енергосистем
КУРСОВА РОБОТА
на тему
"Створення математичної моделі асинхронного генератора в автономному режимі"
по курсу
"Моделювання в енергетиці"
Виконала:
студентка гр. Э-33б
Бернер Г. В.
Перевірив:
доц. Піскурьов М. Ф.
Харьков 2008
Зміст
ВСТУП.........................................................................................................
1. Математична модель асинхронної машини...........................................
2. Дослідження асинхронного генератора в автономному режимі...........
2.1. Загальні положення..........................................................................
2.2. Режим холостого ходу.....................................................................
2.3. Робота з ємнісним навантаженням…………………………………….
ВИСНОВКИ................................................................................................
СПИСОК ДЖЕРЕЛ ІНФОРМАЦІЇ............................................................
ВСТУП
Асинхронні машини найбільшого поширення набули як двигуни. Це основний двигун, що використовується в промисловості, сільському господарстві і в побуті.
В генераторному режимі асинхронні машини застосовуються рідко Основна причина цього в тому, що асинхронна машина не є джерелом реактивної потужності. Для створення магнітного поля в асинхронній машині реактивна потужність поступає з мережі або від конденсаторів.
В асинхронному генераторі, що працює в автономній системі, частота напруги залежить як від частоти обертання ротора, так і від параметрів генератора й елементів автономної системи. Це ускладнює розрахунки режимів роботи автономної системи і проектування асинхронного генератора.
Значні габарити конденсаторів і громіздкі схеми регулювання обмежують застосування асинхронних генераторів в автономних системах. Залежно від співвідношення реактивного опору машини і параметрів зовнішньої мережі самозбудження може характеризуватися плавним ростом напруги й струмів в обмотці статора або мати коливальний характер, при цьому виді самозбудження з'являються биття напруги й струмів у ланцюзі.
У даній роботі зроблена спроба проаналізувати на математичній моделі асинхронного генератора в автономному режимі умови виникнення і протікання процесу самозбудження, зміни параметрів режиму асинхронного генератора в перехідному процесі і кількісні значення цих параметрів в сталому режимі.
1 МАТЕМАТИЧНА МОДЕЛЬ АСИНХРОННОЇ МАШИНИ
Для проектування і експлуатації енергосистем необхідне знання процесів, що відбуваються в енергосистемах, як в нормальному режимі, так і при різних аварійних режимах. Всі ці режими не можуть бути досліджені на реальній енергосистемі, тому для дослідження процесів енергосистема описується за допомогою математичної моделі, яка має схожі з початковою енергосистемою властивості.
Математична модель енергосистеми, навіть з урахуванням всіх можливих спрощень, може виявитися дуже складною для аналітичного розгляду, проте ця ж модель може бути приблизно розрахована за допомогою ЕОМ з достатньою точністю.
У даній курсовій роботі використана модель асинхронного генератора у фазних координатах. Ця модель є системою диференціальних рівнянь зв'язку між струмами і напругою в обмотках асинхронної машини. Модель зручна тим, що в неї входять безпосередньо фазні струми і напруга.
Для моделювання застосований пакет Simulink, що входить в систему Matlab.
У роботі прийнятий ряд допущень.
Допущення, що стосуються моделі АГ:
· частота обертання машини є постійною
· відсутнє магнітне насичення в обмотках машини
· властивості всіх обмоток статора однакові
· враховані тільки обмотки фаз і демпферні обмотки
Моделювання АГ у фазних координатах.
Система рівнянь АГ для напруги у фазних координатах має вигляд:
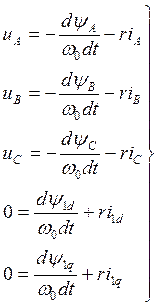 , (1.1)
, (1.1)
де
![]() -
швидкість обертання поля статора;
-
швидкість обертання поля статора;
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() - активні опори обмоток статора
і ротора;
- активні опори обмоток статора
і ротора;
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() - потокозчеплення обмоток статору
і роторних по відповідних осях;
- потокозчеплення обмоток статору
і роторних по відповідних осях;
![]()
![]()
![]()
![]() ,
,![]() - струми
в обмотках статору і роторних по відповідних осях;
- струми
в обмотках статору і роторних по відповідних осях;
![]()
![]()
![]() -
напруга обмоток статору по відповідних осях.
-
напруга обмоток статору по відповідних осях.
У пакеті simulink модель цієї системи виглядає таким чином:
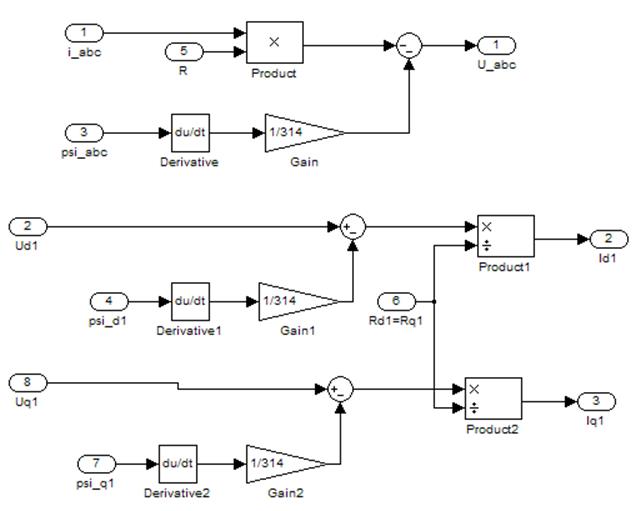
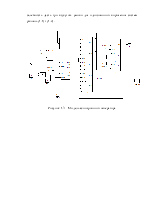
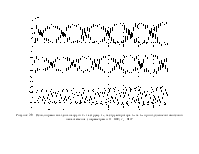
Рисунок 1.1 – Система (1) у пакеті simulink
У верхній частині моделі зображено перші три рівняння системи. Оскільки вони мають однаковий вигляд, для їх опису можна використовувати загальну структурну схему. Це дозволяє зробити модель менш громіздкою. Таке об'єднання сигналів може вважатися вектором. У simulink є можливість застосування поелементних операцій над векторами і над вектором і числом. Ця модель і інші буде підсистемою іншої моделі, для зовнішньої моделі будуть доступні тільки входи (In) і виходи (Out).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.