4 УРОВНЕНИЯ ПЕРЕХОДНОГО ПРОЦЕССА СИНХРОННОЙ МАШИНЫ В ФАЗНЫХ КООРДИНАТАХ
4.1 Общие замечания и допущения
Аналитическое исследование переходных процессов машины с учетом всех влияющих на них факторов представляет сложную задачу. Чтобы несколько упростить ее, приходится вводить ряд допущений, придавая машине некоторые свойства и качества, которыми она в действительности не обладает, т.е. рассматривать в известной мере « идеализированную » машину.
Рассматриваемые в данном разделе математические модели синхронного генератора (СГ) составлены при следующих допущениях:
1. Магнитная система машины ненасыщенна, в силу чего индуктивности машины не зависят от намагничивающих сил (н.с).
2. Вместо действительных кривых распределения н. с. и индукции в воздушном зазоре по расточке статора принимают только их основные, первые гармонические, соответственно чему наведенные в статоре ЭДС выражаются синусоидами основной частоты.
3. В магнитной системе машины отсутствуют какие-либо потери.
4. Конструктивное выполнение машины обеспечивает полную симметрию фазных обмоток статора и ротора.
При этих допущениях наиболее точной будет модель СГ в фазных координатах А, В, С.
4.2 Исходные уравнения
Дифференциальные уравнения равновесия ЭДС и падений напряжений в каждой из обмоток будут:
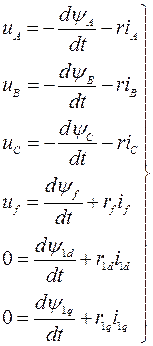(4.1)
где 
-
активные сопротивления соответственно для контуров каждой
фазы, цепи возбуждения и демпферных обмоток;
- результирующие потокосцепления
соответствующих обмоток (включая их потокосцепления рассеяния).
Потокосцепления, при принятых допущениях представляют собой линейные зависимости от тока данного контура и токов магнитносвязанных с ним других контуров. Коэффициентами пропорциональности при этом будут индуктивность L рассматриваемого контура и его взаимоиндуктивности М с другими контурами.
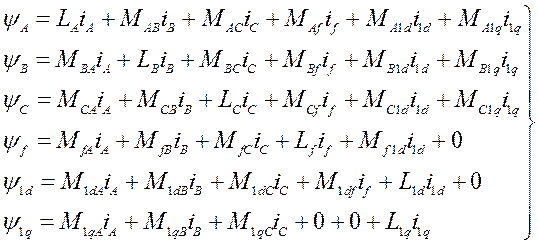(4.2)
Во вращающейся
машине только индуктивности 
можно считать
постоянными. Все же остальные Lи М
зависят от положения ротора относительно обмоток статора и, следовательно,
являются функциями времени.
После подстановки потокосцеплений из (4.2) в систему уравнений (4.1) получим систему дифференциальных уравнений с переменными коэффициентами.
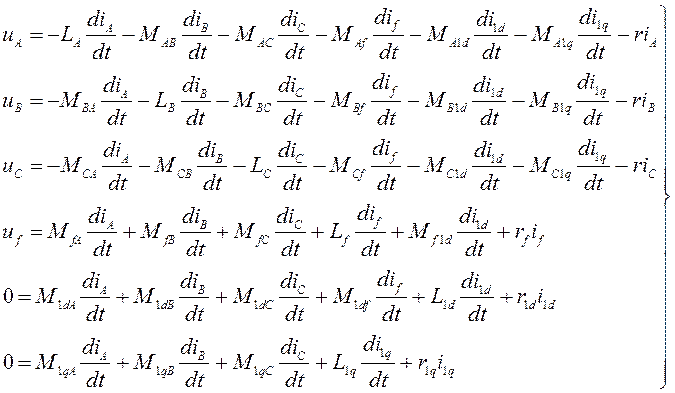(4.3)
Наличие переменных коэффициентов, резко усложняет решение этой системы. Поэтому до последнего времени эта математическая модель СГ практически не использовалась.
4.1 Индуктивности обмоток синхронной машины
Исходя из уравнений (4.1), (4.2), (4.3), в качестве примера, на рисунке 4.1 представлен верхний уровень структурной схема математической модели синхронного генератора в фазных координатах. С целью упрощения в этой модели не учитываются демпферные обмотки. Как видно из рисунка структурная схема состоит из 4 субсистем, каждая из которых реализует расчет определенных величин:
Субсистема 1 (рисунок 4.2) реализует расчет соответствующих индуктивностей и взаимоиндуктивностей. В свою очередь субсистема 1 состоит из четырех подсистем (1.1-1.4), приведенных на рисунках 4.3-4.6.
Виртуальная модель, приведенная на рисунке 4.5, реализует решение уравнений
,
,
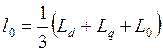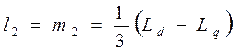(4.4)
.
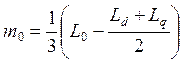и позволяет рассчитать постоянные составляющие соответствующих индуктивностей (l0и m0) и амплитуды вторых гармоник тех же индуктивностей (l2и m2).
Виртуальная модель, приведенная на рисунке 4.4, реализует решение системы уравнений 2.5:
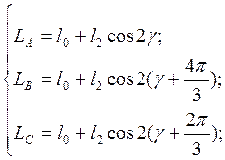(4.5)
и позволяет рассчитать индуктивности La,Lb,Lc.
Виртуальная модель, приведенная на рисунке 4.5, реализует решение системы уравнений 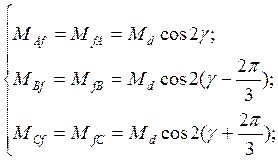4.6:
(4.6)
и позволяет рассчитать взаимоиндуктивности между обмотками статора Mab, Mac, Mbc.
Виртуальная модель, приведенная на рисунке 4.6, реализует решение системы уравнений 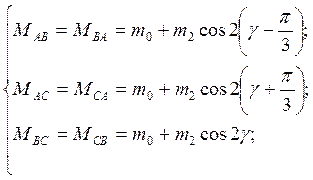4.7:
(4.7)
и позволяет рассчитать взаимоиндуктивности между обмоткой возбуждения и обмотками статора Maf, Mbf, Mcf.
На рисунке 4.7 приведена субсистема 2 расчета потокосцеплений соответствующих обмоток генератора, реализующая решение системы уравнений 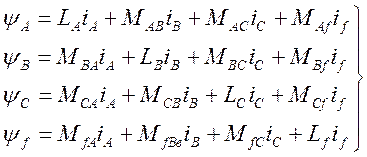4.8:
(4.8)
Эта субсистема состоит из четырех подсистем 2.1-2.4. В качестве примера на рисунке 4.8 приведена модель расчета потокосцепления фазы А в соответствии с уравнением 1 системы 4.8 (подсистема 2.1). Подсистемы 2.2-2.4 расчета потокосцепления фаз В. С и обмотки возбуждения по своей структуре аналогичны подсистеме 2.1.
4.4 Математическая модель СГ в фазных координатах реализованная в пакете Matlab
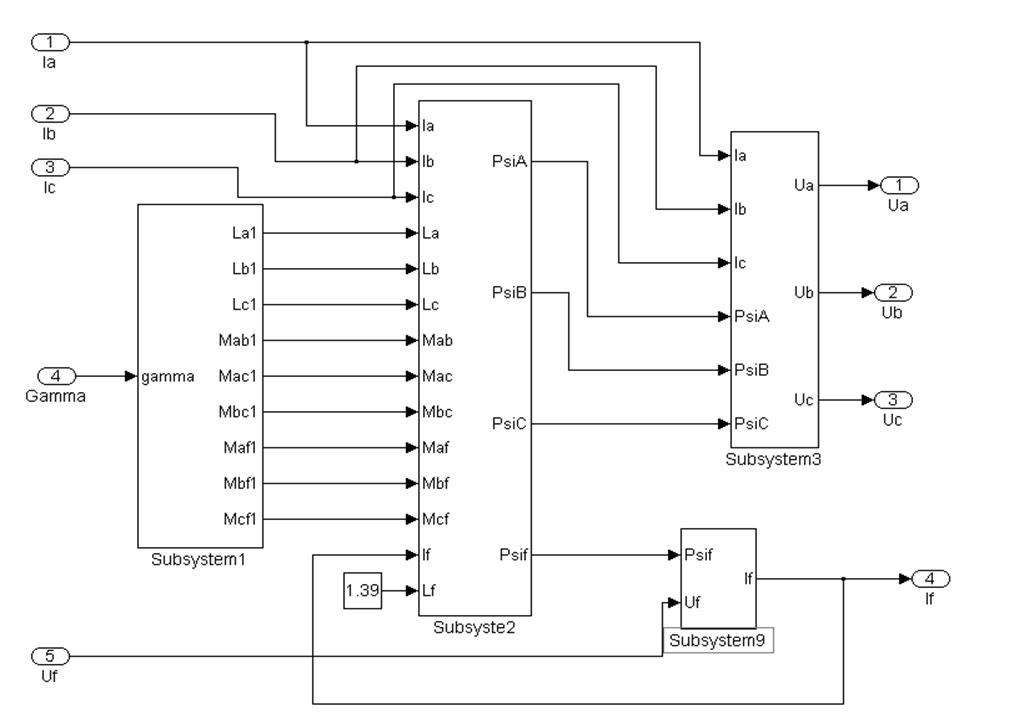
Рис 4.1 Структурная схема синхронного генератора в координатах 
в режиме холостого хода
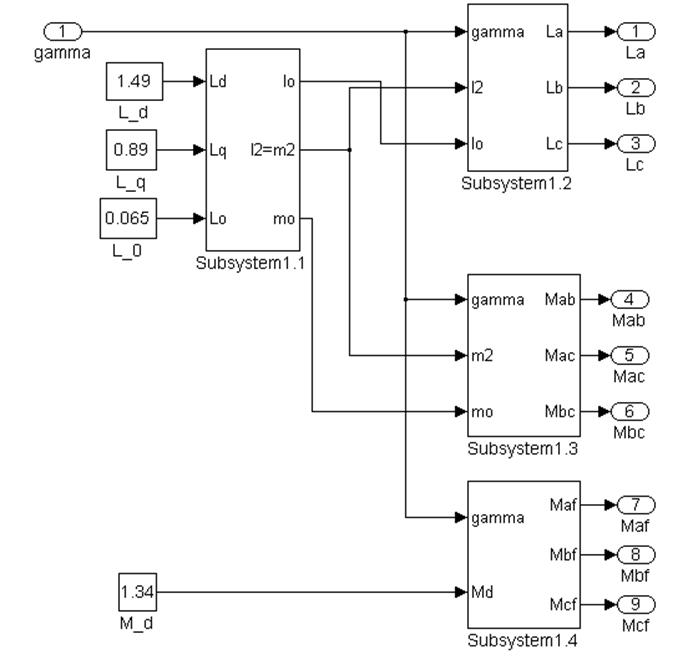
Рис 4.2 Субсистема 1.Структурная схема расчета индуктивностей и взаимоиндуктивностей.
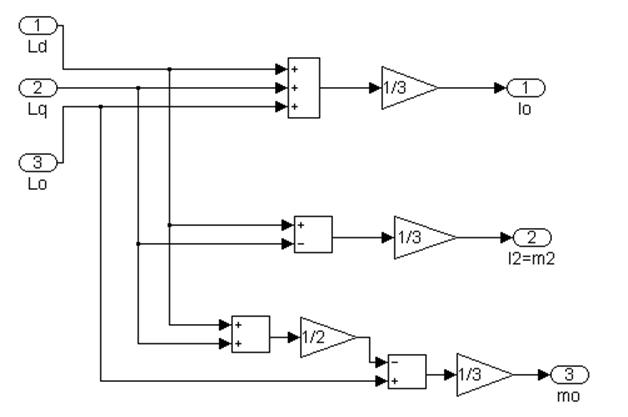
Рис 4.3 Подсистема 1.1. Расчет коэффициентов
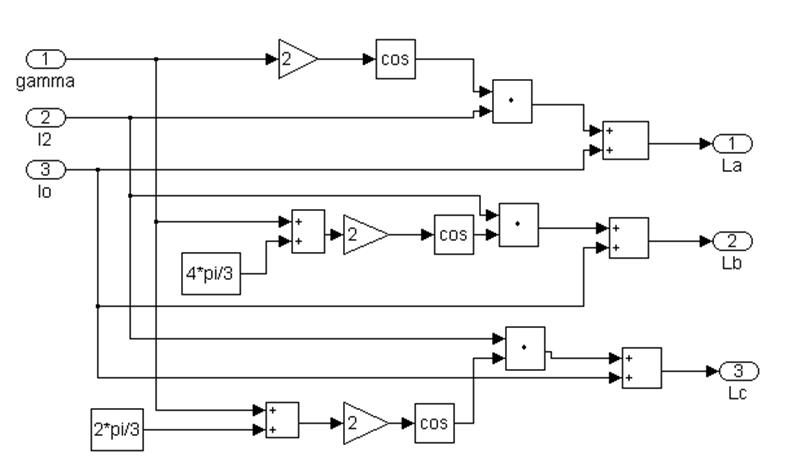
Рис 4.4 Подсистема 1.2. Расчет индуктивностей La,Lb,Lc
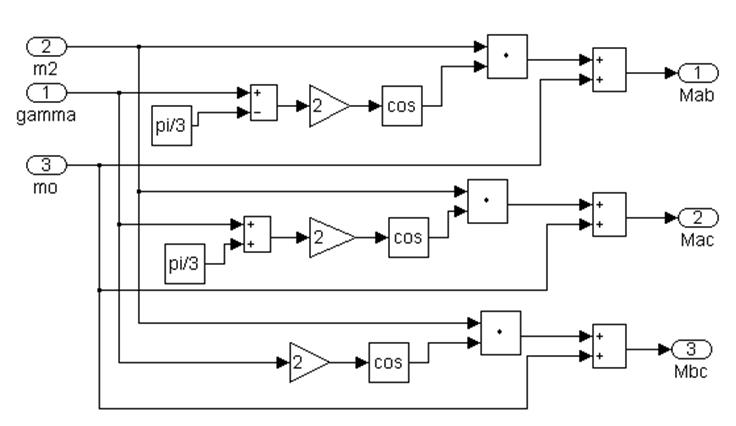
Рис 4.5 Подсистема 1.3. Расчет взаимоиндуктивностей между обмотками статора Mab, Mac, Mbc
Эта модель и многие последующие будет являться подсистемой другой модели, для внешней модели будут доступны только входы (In) и выходы (Out).
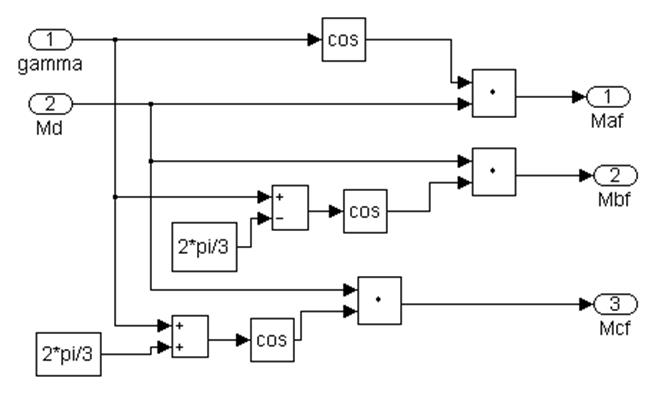
Рис 4.6 Подсистема 1.4. Расчет взаимоиндуктивностей между обмоткой возбуждения и обмотками статора Maf, Mbf, Mcf.
На рисунке 4.9,субсистема 3 реализует решение системы уравнений 4.9 и позволяет смоделировать фазные напряжения генератора.
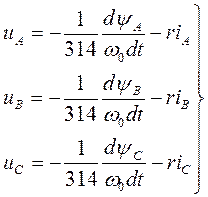(4.9)
Субсистема 4, представленная на рисунке 4.10, моделирует ток в обмотке возбуждения в соответствии с уравнением:
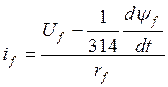(4.10)
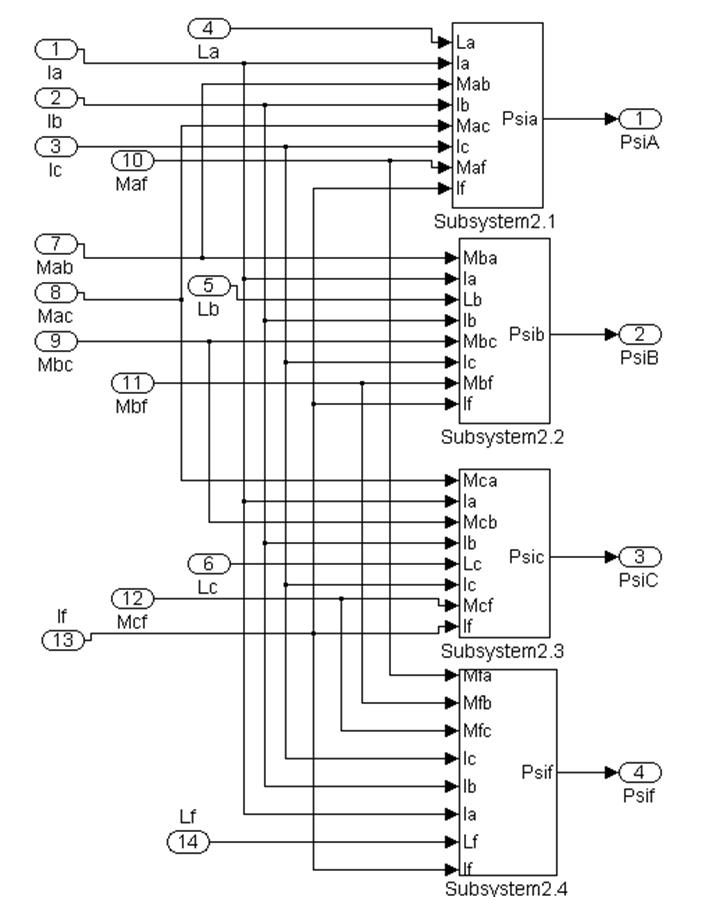
Рис 4.7 Субсистема 2 Структурная схема расчета потокосцеплений
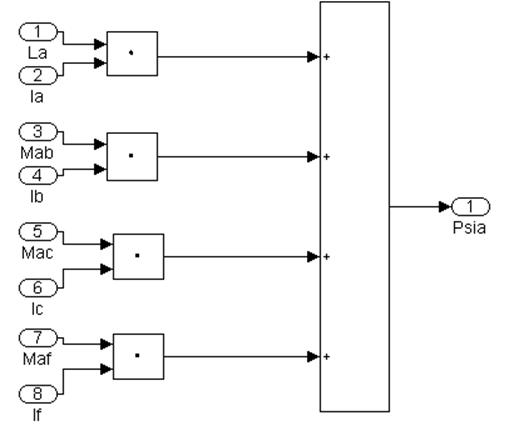
Рис 4.8. Подсистема 2.1. Расчет потокосцепления фазы А.
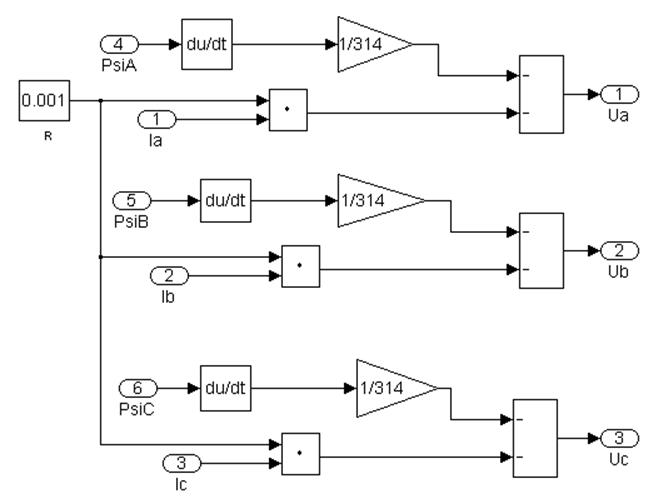
Рис 4.9 Субсистема 3. Расчет фазных напряжений генератора.
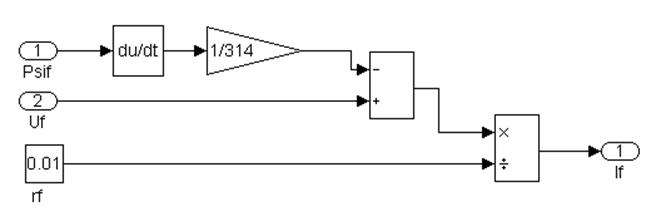
Рис 4.10. Субсистема 4. Расчет тока в обмотке возбуждения
Модель генератора можно составить как подсистему, состоящую из описанных выше подсистем.
При этом выходными параметрами модели будут напряжения в фазах
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
