Створення математичної моделі асинхронного генератора в автономному режимі, страница 2

Потокозчеплення визначені як добуток струмів на відповідні індуктивності і взаємоіндуктивності:

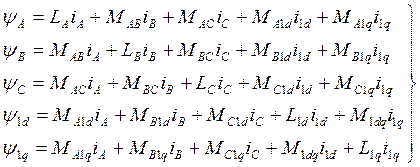,                     (1.2)

де M і L - відповідні індуктивності і взаємоіндуктивності.

Для спрощення моделювання цієї системи можна об'єднати струми фаз і роторних обмоток в п’ятивимірний вектор, тоді кожне з рівнянь буде скалярним добутком цього вектора на інший вектор, що складається з індуктивності і взаємоіндуктивностей.

Рисунок 1.2 – Система (2) у пакеті simulink

Елемент Dot Product - реалізує скалярний добуток векторів, при цьому сигнали, об'єднані за допомогою елементу Mux, автоматично вважаються векторами.

У машині, що обертається, тільки взаємоіндуктивності між ротором і статором залежать від положення ротора щодо обмоток статора і, отже, є функціями часу. Решту L і М можна вважати незмінною.

;                                   (1.3)

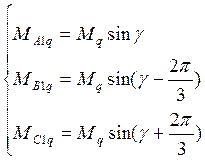.                                    (1.4)

Тут блоком constant заданий вектор кутів, при яких відповідні індуктивності максимальні. При проведенні математичних операцій з вектором всі операнди-числа при необхідності автоматично перетворяться у вектора цієї ж розмірності, так що збільшення до вектора число, використовуючи суматор, коректно. Таким же чином можна побудувати підсистеми для розрахунку взаємоіндуктивностей.

Складові індуктивностей можна виразити через індуктивності, якими зазвичай характеризується синхронна машина:

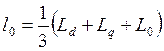                                           ;                                           (1.5)

                                           .                                       (1.6)

Модель генератора можна скласти як підсистему, що складається з описаних вище підсистем.

При цьому вихідними параметрами моделі буде напруга у фазах. Вхідними параметрами напруги будуть струми у фазах. Залежність струмів від напруги визначатиметься режимом роботи енергосистеми, модель режиму роботи розташовуватиметься поза моделлю генератора. Ця залежність дасть три відсутніх умови для однозначного вирішення систем рівнянь (1.1) і (1.2).

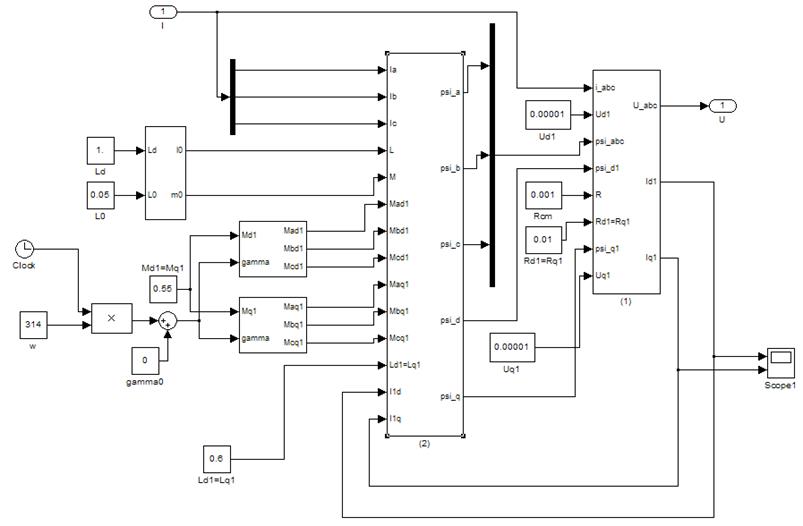
Рисунок 1.3 – Модель асинхронного генератора

2 ДОСЛІДЖЕННЯ АСИНХРОННОГО ГЕНЕРАТОРА

У АВТОНОМНОМУ РЕЖИМІ

2.1 Загальні положення

Дослідження проводилися при наступних допущеннях:

- не враховувалося насичення магнітної системи асинхронної машини, тому сталий режим не наступав, і фіксувався тільки факт відсутності або появи самозбудження;

- враховувався вплив на параметри режиму самозбудження тільки одного чинника, інші при цьому вважалися постійними. Наприклад, змінювали ємність, а частота обертання ротора, активний і індуктивний опори зовнішнього ланцюга статора не змінювалися;

- розрахунок проводився у відносних одиницях.

АГ працює у автономному режимі коли до його шин підключається лише ізольоване навантаження, тобто він не має зв'язку з системою. В цьому режимі струм у ланцюгах генератора та навантаження з'являється за рахунок процесу самозбудження. Одна із умов виникнення самозбудження – наявність залишкової індукції у роторі. У математичній моделі залишкова індукція у роторі моделюється поданням на ротор невеликої напруги, значення якої дорівнює 0,00001. Для цього використовується елемент Constant.

Для виникнення самозбудження також необхідно обертання ротора з частотою, близькою до номінальної. У математичній моделі це досягнуто за рахунок моделювання змінних у часі взаємоіндуктивностей  та , які змінюються відповідно по косинусоїдальному та синусоїдальному законам з частотою 314. Схема що моделює змінні взаємоіндуктивності, приведена на рисунку 2.1:

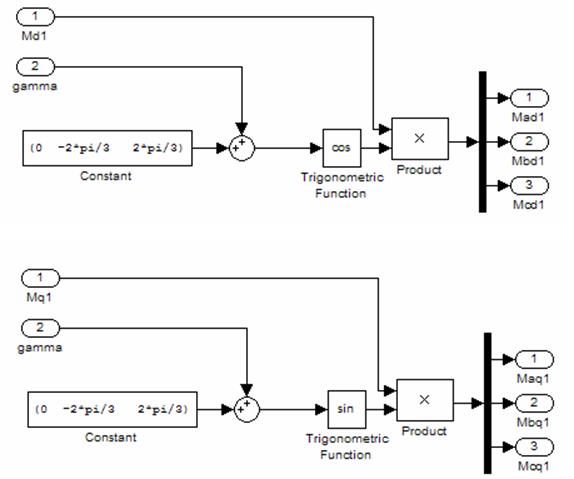
Рисунок 2.1 – Схема що моделює змінні взаємоіндуктивності

Результати досліджень показані на трьох осцилограмах: вихідного струму у фазі А, вихідної напруги тієї ж фази, а також струмів ротору, які виводились на одну осцилограму.