Расчет несимметричного короткого замыкания

2. РАСЧЕТ НЕСИММЕТРИЧНОГО КОРОТКОГО ЗАМЫКАНИЯ

При расчете несимметричного КЗ применяется метод симметричных составляющих.

Если необходимо определить токи и напряжения для произвольных моментов времени не только  в точке КЗ, но и в местах, удаленных от точки КЗ, то применяют метод спрямленных характеристик.

2.1. Расчет действующего значения периодической составляющей тока и напряжения однофазного КЗ в точка К2 для момента времени t=0,2c.

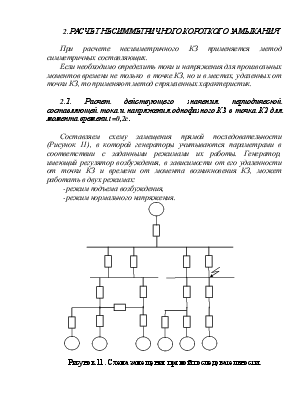
Составляем схему замещения прямой последовательности (Рисунок 11), в которой генераторы учитываются параметрами в соответствии с заданными режимами их работы. Генератор, имеющий регулятор возбуждения, в зависимости от его удаленности от точки КЗ и времени от момента возникновения КЗ, может работать в двух режимах:

-режим подъема возбуждения,

-режим нормального напряжения.

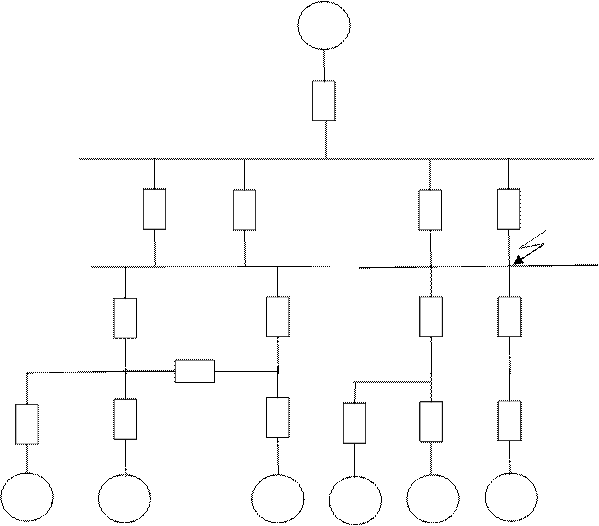Рисунок 11. Схема замещения прямой последовательности.

Если t0,5с, то можно считать, что все генераторы работают в  режиме подъема возбуждения. Параметры генераторов в этом случае ЭДС  и сопротивлением , которые определяем  по спрямленным характеристикам (рис.4.1  [1]) в зависимости от заданного момента времени t и величины заданного предшествующего тока возбуждения . Значения даны в относительных единицах по отношению к номинальной мощности генераторов, поэтому их необходимо привести к базисным условиям. При t=0,2c.и =2,2 и 2,0 для соответствующих генераторов о по спрямленным характеристикам получаем для генераторов Г1, Г2 и  для генератора Г3.

Нагрузка в схеме замещения учитывается сопротивлением  и ЭДС = 0.

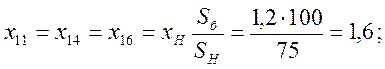
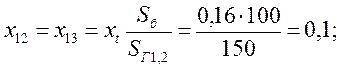
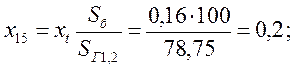
Так как сопротивлениенагрузки на порядок больше сопротивлений других элементов, все нагрузочные ветви отбрасываем. Получим схему замещения представленную на рисунке 12.

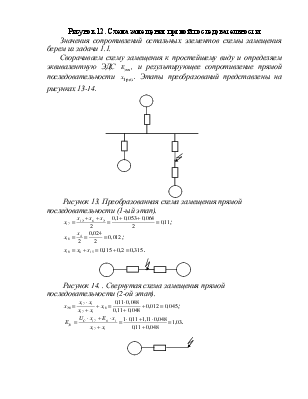
Рисунок 12. Схема замещения прямой последовательности.

Значения сопротивлений остальных элементов схемы замещения берем из задачи 1.1.

Сворачиваем схему замещения к простейшему виду и определяем эквивалентную ЭДС , и результирующее сопротивление прямой последовательности . Этапы преобразований представлены на рисунках 13-14.

Рисунок 13. Преобразованная схема замещения прямой последовательности (1-ый этап).

;

;

.

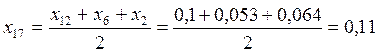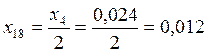Рисунок 14. . Свернутая схема замещения прямой последовательности (2-ой этап).

;

.

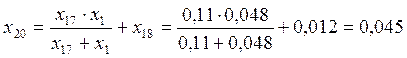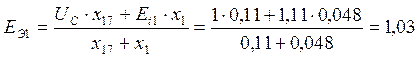Рисунок 15. . Свернутая схема замещения прямой последовательности.

;

.

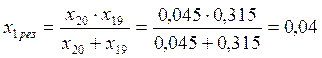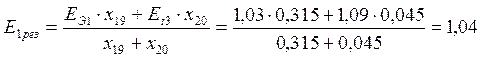Составляем схему замещения обратной последовательности (рисунок 16. Схема  замещения обратной последовательности по своей конфигурации аналогична схема  замещения прямой последовательности, но в ней отсутствуют источники ЭДС и сопротивления генераторов рассчитываются по формуле:

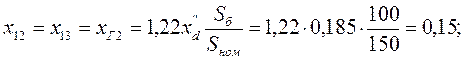
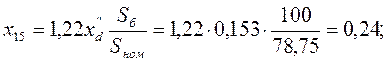
Рисунок 16. Схема замещения обратной последовательности.

Преобразовываем схему замещения обратной последовательности и находим ее результирующее сопротивление. Этапы преобразований представлены на рисунках 17-19.

;

.

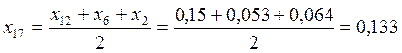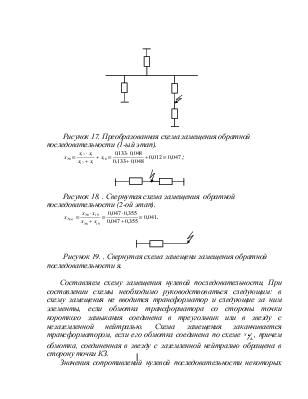
Рисунок 17. Преобразованная схема замещения обратной последовательности (1-ый этап).

;

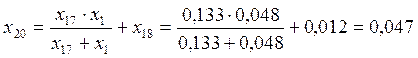Рисунок 18. . Свернутая схема замещения  обратной последовательности (2-ой этап).

.

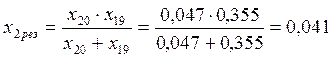Рисунок 19. . Свернутая схема замещени замещения обратной последовательности я.

Составляем схему замещения нулевой последовательности, При составлении схемы необходимо руководствоваться следующим: в схему замещения не вводится трансформатор и следующие за ним элементы, если обмотка трансформатора со стороны точки короткого замыкания соединена в треугольник или в звезду с незаземленной нейтралью. Схема замещения заканчивается трансформатором, если его обмотка соединена по схеме , причем обмотка, соединенная в звезду с заземленной нейтралью обращена в сторону точки КЗ.

Значения сопротивлений нулевой последовательности некоторых элементов, выраженные через сопротивления прямой последовательности, приведены в таблице 4.1.[1]

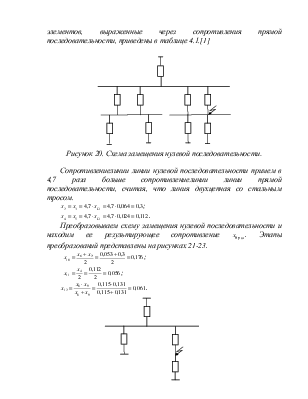
Рисунок 20. Схема замещения нулевой последовательности.

Сопротивлениелинии линии нулевой последовательности примем в 4,7 раза больше сопротивлениелинии линии прямой последовательности, считая, что линия двухцепная со стальным тросом.

;

.

Преобразовываем схему замещения нулевой последовательности и находим ее результирующее сопротивление . Этапы преобразований представлены на рисунках 21-23.

;

;

.

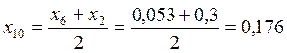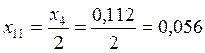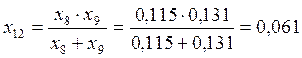Рисунок 21. Преобразованная схема замещения нулевой последовательности (1-ый этап).

.

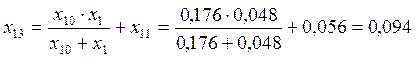Рисунок 22. Свернутая схема замещения  нулевой последовательности (2-ой этап).

.

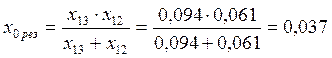Рисунок 23. Свернутая схема замещени замещения  нулевой последовательности я.

Определяем ток прямой последовательности особой фазы однофазного КЗ в относительных единицах.

.

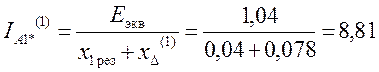где  сопротивления шунта.

Определяем ток прямой последовательности особой фазы однофазного КЗ в (КА).

Определяем модуль тока поврежденной фазы однофазного КЗ в КА.

;

где .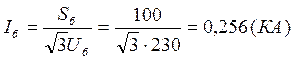

Рассчитываем напряжение прямой последовательности особой фазы в  относительных единицах

Рассчитываем напряжения обратной и нулевой последовательностей особой фазы в  относительных единицах

Умножив напряжения всех последовательностей в относительных единицах на базисное напряжение получим напряжения в (КВ).

Строим векторные диаграммы токов и напряжений в точке КЗ (приложение 1 и 2).

2.2. Расчет действующего значения периодической составляющей тока в указанном сечении и напряжения в указанном узле для заданного момента времени.

Используя значения симметричных составляющих тока и напряжения в точке КЗ из задачи 2.1, разворачиваем поочередно схемы замещения прямой, обратной и нулевой последовательностей и находим составляющие токов в сечении F-F и составляющие напряжений в точке “M”.

Рассчитываем ток прямой последовательности фазы А в сечении    F-F.

;

;

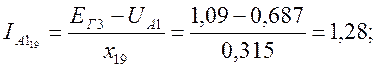
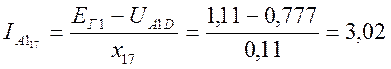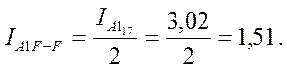
Рассчитываем ток обратной последовательности фазы А в сечении    F-F.

;

;

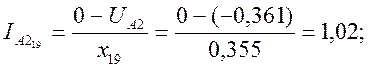
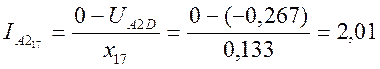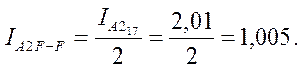
Рассчитываем ток нулевой последовательности фазы А в сечении    F-F.

;

;

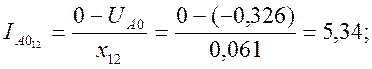
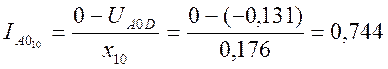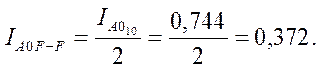
2.2.1 Построение векторных диаграмм токов в сечении и напряжений в точке.

Если трансформатор, за которым расположена точка “M” имеет схему соединения обмоток  - 11, то при переходе через векторы напряжения прямой последовательности должны быть повернуты на 30⁰ против хода часовой стрелки, а векторы напряжения обратной последовательности - на 30⁰ по ходу часовой стрелки.

Фазные токи в сечении F-F определяем геометрическим суммированием симметричных составляющих токов, при этом вектор тока прямой последовательности особой фазы направляем по вещественной оси. Векторная диаграмма токов в сеченииF-F представлена в приложении 3.

Фазные напряжения в точке “M” определяем геометрическим суммированием симметричных составляющих всех последовательностей, при этом вектор напряжения прямой последовательности направляем по мнимой оси. Векторная диаграмма напряжений в точка “M” представлена в приложении 4.