Анализ статической устойчивости. Анализ динамической устойчивости электро-энергетической системы

АНАЛИЗ СТАТИЧЕСКОЙ УСТОЙЧИВОСТИ.

Все расчеты проводятся в пренебрежении активным сопротивлением передачи, поэтому в начале и конце передачи равны. Потери же реактивной мощности в передаче имеют место. Поэтому меньше в конце передачи, чем в ее начале.

Расчет ведется в относительных единицах по формулам точного приведения. В качестве базисных величин рекомендуется принять: , . Базисная мощность только численно равна мощности .

Параметры элементов схемы замещения и параметры режима, приводятся к ступени напряжения  [3].

5.1. Расчет предела передаваемой мощности и коэффициент запаса статической устойчивости без учета нагрузки.

При отсутствии нагрузки ЭЭС является простейшей.

5.1.1. Генераторы станции не имеют АРВ.

Порядок расчета:

-Составляем схему замещения, в которой генераторы задаются синхронными параметрами ЭДС - и сопротивлениями , и рассчитываем ее параметры.

Сопротивление генераторов –

.

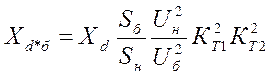Сопротивление трансформаторов –

.

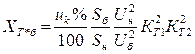Сопротивление линии –

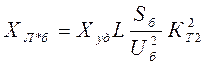, где - удельное сопротивление линии (Ом/км).

Сопротивление автотрансформатора-

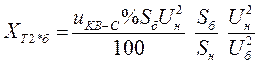
В дальнейших расчетах индекс " * " при соответствующих величинах опустить, т.к. действия проводятся только с относительными базисными величинами.

- Сворачиваем схему замещения к простейшему виду   и рассчитываем суммарное сопротивление передачи.

, где - сопротивление связи генераторов с системой.

- По известным и рассчитывают модуль ЭДС эквивалентного генератора  по формуле

, аргумент:

;

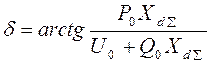- Задавая углы  от 0 до  строим угловую характеристику мощности по формуле:

Рассчитываем предел передаваемой мощности:

Предел статической устойчивости  (из уравнения ).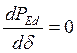

Коэффициент запаса статической устойчивости:

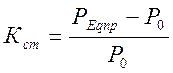
5.1.2. Генераторы станции  имеют АРВ пропорционального действия.

Порядок расчета:

-Составляем схему замещения, в которой генераторы задаются переходными параметрами ЭДС - и сопротивлениями, и рассчитываем сопротивления генераторов

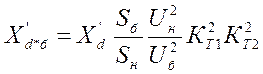
- Сворачиваем схему замещения к простейшему виду  и рассчитываем суммарное сопротивление передачи.

,

- Рассчитываем Модуль ЭДС:

Где    ,

;

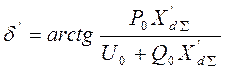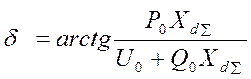
- Задавая углы  от 0 до , строим характеристику мощности по формуле

.

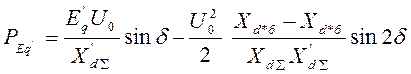Предел статической устойчивости определяют из условия:

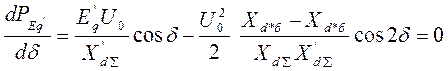         при

Замечание. В последнем уравнении неизвестная величина  входит  под знак косинуса. Перейдя от косинуса двойного угла к косинусу одинарного угла и, решив квадратное уравнение относительно косинуса искомого угла, получим.

,

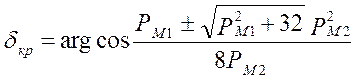Где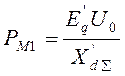     

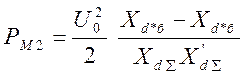
- Рассчитываем предел передаваемой мощности  путем подстановки  угла . В формулу характеристики мощности.

- Рассчитываем коэффициент запаса статической устойчивости

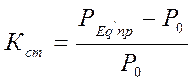
5.1.3. Генераторы станции имеют  АРВ сильного действия.

Порядок расчета:

-Составляем схему замещения, в которой генераторы задаются напряжением  и сопротивлением равным нулю.

- Рассчитываем модуль напряжения  :

где    ,

;

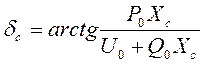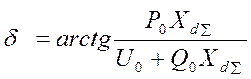
- Задавая углы  от 0 до , строим характеристику мощности по формуле

.

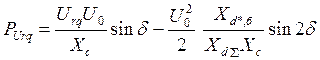Предел статической устойчивости определяем из условия:

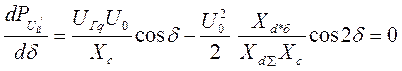         при

,

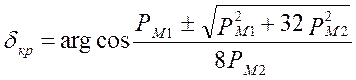Где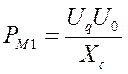     

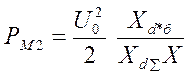
- Рассчитываем предел передаваемой мощности  путем подстановки  угла . В формулу характеристики мощности.

- Рассчитываем коэффициент запаса статической устойчивости

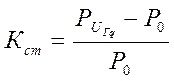
5.2. Расчет предел передаваемой мощности и коэффициент запаса статической устойчивости cучетом нагрузки.

Включение нагрузки превращает исследуемую систему в сложную.  Поэтому следует воспользоваться выражением угловой характеристики мощности генератора, работающего в сложной системе.

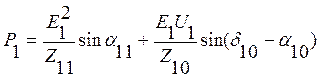
5.2.1. . Генераторы станции  имеют АРВ пропорционального действия.

Порядок расчета:

-Составляем схему замещения, в которой генераторы задаются переходными параметрами ЭДС - и сопротивлениями рис. 5.1.

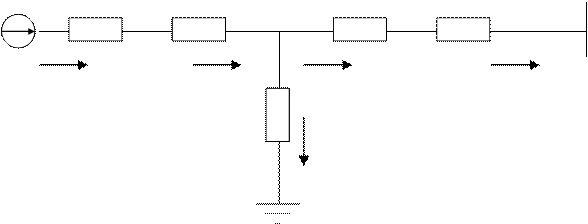Е¹              X_Г                      X_Т1U_Н            X_ЛX_Т2

U_О

Р_1Н, Q_1Н                  Р_1О, Q_1О            Р_О, Q_О

Z_Н

Р_Н, Q_Н

                     

Рисунок 5.1.Схема замещения электропередачи с учетом нагрузки.

Сопротивление нагрузки равно:

;

;

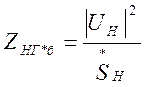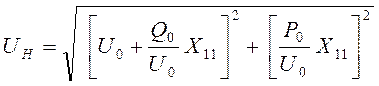где  ;

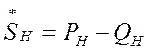   -сопряженный комплекс мощности нагрузки.

Сопротивления других элементов схемы замещения взять из задачи 5.1.2.

- Рассчитываем мощности протекающие в системе.

Мощность, вытекающая из узла нагрузки в систему отличается от на величину потерь реактивной мощности в сопротивлении.

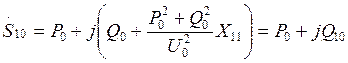
Мощность, притекающая к узлу нагрузки от электростанции:

- Рассчитываем ЭДС генератора без АРВ:

;

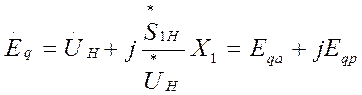Модуль ЭДС   и аргумент  равны:

;               

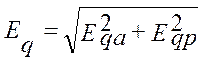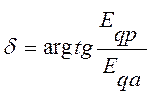
где - сопряженный комплекс мощности, притекающей к узлу нагрузки;

- сопряженный комплекс напряжения на шинах нагрузки;

               

- Рассчитываем ЭДС генератора без АРВ:

;

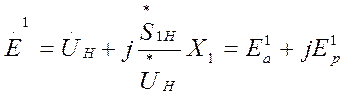Модуль ЭДС   и аргумент  равны:

;               

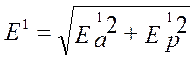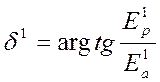
Модуль ЭДС 

Комплексные значения собственного и взаимного сопротивлений Z₁₁ и Z₁₀ определяем методом преобразований  схемы рис. 5.1 по формулам:

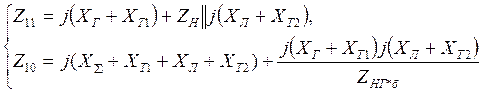
По найденным комплексным сопротивлениям определяют их моду-  ли. Углы  и рассчитывают по формулам:

,

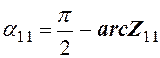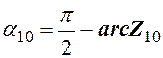
Предел передаваемой мощности генератора в сложной системе имеет  значения:

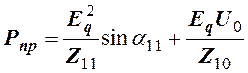
Предел статической устойчивости  наступает при выполнении условия:

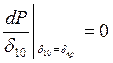 т.е. при

Коэффициент запаса статической устойчивости определяют так же, как в п.5.1.

Полученные результаты необходимо представить в виде таблицы и сделать выводы о влиянии АРВ и нагрузки на предел передаваемой мощности, предел статической устойчивости и коэффициент запаса статической устойчивости.

Таблица 1

Наличие и тип АРВ
	без нагр.	с нагр.	без нагр.	с нагр.	без нагр.	с нагр.
без АРВ	+		+		+
с АРВ пропорционального типа	+		+		+
с АРВ сильного действия	+		+		+

6. АНАЛИЗ ДИНАМИЧЕСКОЙ УСТОЙЧИВОСТИ ЭЛЕКТРО-

ЭНЕРГЕТИЧЕСКОЙ СИСТЕМЫ