1.Режим подъема возбуждения ему соотв. прямой NtT´.
Параметры:Et,Xt.
2.Режим нормального напряжения.
Соответствует N0nt.
Расчетные параметры:
E=Uн;
X=0;
Для решения о режиме работы, необходимо сравнить его внешнюю реактивность с критической.
Если:
Xвн≤Xкрt, то Г раб. в режиме подъема возбуждения
Xвн≥Xкрt, режим нормального напряжения;
Если:
Xвн=Xкрt, то выполняется условие двух режимов.
Величина
Xкрt находится как и для установленного режима. 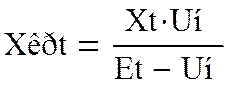
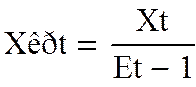
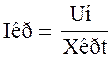
Величина
Параметры Et, Xt находим по кривым в участке Ульянова.
Техника расчета.
Составляют схему замещения, в которую Г без АРВ вводят Et, Xt.
Г с АРВ вводят в зависимости от режима работы либо Et, Xt- в случае режима подъема возбуждения. Либо E=Uн; X=0- в случае реал. норм. напр.
Для выбора режима необходимо сравнить Xвн и Xкрt. Но в сложных схемах,
Xвн для каждого Г не может быть определено. Поэтому расчет ведется методом последовательных приближений. Сначала режимами работы попросту задаются, анализируя схему. Если момент времени < 0.5с, то инерционность схемы с АРВ, можно принимать режим подъема возбуждения. Затем , сворачиваем схему относительно места короткого замыкания, находят EtΣ, XtΣ.
После чего вычисляют Int в месте короткого замыкания.
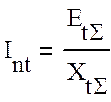
и находим распределение токов в схеме. Затем проводят проверку режимов работы Г.
Для Г, работа в режиме возбуждения.
![]()
Для Г, работа в режиме нормального напряжения.
![]()
Если режим работы хотя бы одного Г не подтверждается, необходимо провести повторный расчет по методу последовательной приближ. Основным и принципиальным допущением метода спрямленных характеристик является, то, что параметры Et, Xt получили для простейшей схемы, используем для схемы с несколькими Г. , но всё равно этот метод более точен, чем метод расчетных кривых. Возможны также и некоторые уточнения. В частности, на постоянную времени Tf0. Если Tf0 Г отличается в 1.5 и более раз отличается от Tf0 кривых, то надо находить Et, Xt для момента времени t:
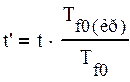
Электромагнитные переходные процессы при нарушении симметрии трёх фазной цепи.
Несимметрия является однократной. Они происходят только в одном месте. Может быть либо поперечной (несимметричное короткое замыкание различных видов) и продольной (разрыв одной двух фаз). Будем говорить ноль.
Однократной поперечной несимметричной.
Несимметричное к.з. в отличии от трех фазного создает различные условия для фаз. С-ма фазных токов и напряжений будут несимметричными. Углы сдвига по фазе между напряжением и током будут различными.
Обычно анализ несимметричных режимов ведётся методом симметричных составляющих. Анализ прост, но в применении к расчету несимметричных п.п. еще требует обоснования. Но этот метод обеспечивает сведение несимметричных к.з. к некоторому фиктивному трех фазному к.з.
Основные положения метода.
Любую несимметричную систему E, I, U, Ψ трех фазной цепи можно однозначно представить как сумму трех симметричных систем- систем прямого следования фаз, обратного, нулевого, которое коротко называется симметричными составляющими.
Графически это можно представить так:
 |
Математически:
F´A=F´A1+F´A2+F´A0
F´B=F´B1+F´B2+F´B0
F´C=F´C1+F´C2+F´C0
Можно принять какую-то составляющую за основную, а две другие выразить через неё:
a=1·ej120
FA=FA1+FA2+FA0
FB=a2FA1+aFA2+FA0
FC=aFA1+a2FA2+FA0
Выразим симметричные составляющие через несимметричные.
FA0=⅓·(FA+FB+FC)
FA1=⅓·(FA+aFB+a2FC)
FA2=⅓·(FA+a2FB+aFC)
Системы величин прямой и обратной последовательности является симметричными и уравновешенными системами. А системы величин нулевой последовательности- симметричными, но неуравновешенными. Они характеризуются соотношением:
FA+FB+FC≠0
Т.о. система нулевой последовательности может быть в составе только неуравновешенной.
Составляющие нулевой последовательности появляются только в том случае, если к.з. связано с землей. Система фазных напряжений тоже содержит нулевую последовательность при к.з. на землю. Система междуфазных напряжений всегда уравновешена, в составе никогда не содержит нулевых составляющих.
Применимость метода симметричных составляющих к анализу несимметричных п.п.
Все элементы электрической схемы являются симметричными т.е. сопротивление фаз элементов одинаковы. Это упрощает применение метода симметричных составляющих, потому что при выполнении этого условия каждую последовательность величин можно рассчитывать независимо, т.к. системы токов, связанные законами Ома, Кирхгофа и т.д. с системами напряжений только одноименной последовательности. Если предположить что какой либо элемент схемы обладает по отношению к системам тока прямой, обратной, нулевой последовательности сопротивлениями Z1,Z2,Z0 соответственно, то симметричные составляющие падения напряжения на этом элементе можно записать в следующем виде:
ΔŮ1=İ1z1 ΔŮ1=jİ1x1
ΔŮ2=İ2z2 ΔŮ2=jİ2x2
ΔŮ0=İ0z0 ΔŮ0=jİ0x0
Эти сопротивления называются сопротивлениями в отношении систем токов. Коротко: сопротивление нулевой, обратной, прямой последовательности.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.