Реализация схемных мероприятий по оптимизации системы и повышению ее точности в статических режимах

Министерство высшего образования Российской Федерации

Санкт-Петербургский Государственный Политехнический Университет

Электромеханический факультет

Кафедра “Электрические сети и системы”

Курс “Теория автоматического регулирования”

Пояснительная записка

по курсовой работе

Вариант № 4

Выполнили:

Студенты группы 3023/1

Лукьяненко М.Н.

Шескин Е.Б.

Проверил: Попков Е.Н.

Санкт-Петербург

2006

Параметры нагрузки:C=1000 мкФ,R=1.5 Ом,R₀=2.5

Номинальное значение регулируемой переменной в установившемся режиме: I=1000 A

Пункт 1

I.Операторное пространство

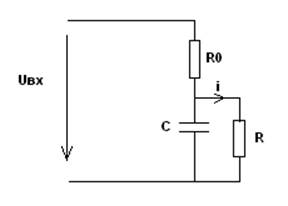X_вых=i

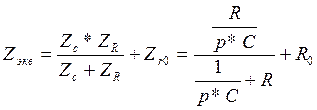
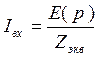
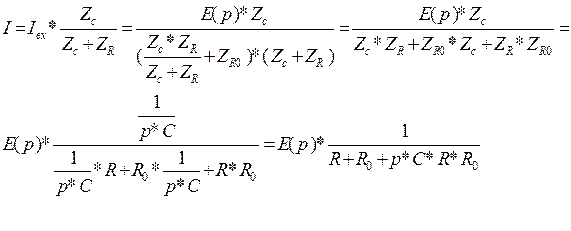
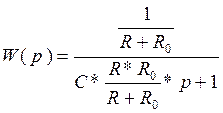
2.Физическое пространство.

1)Компонентные уравнения:

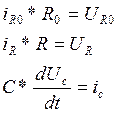
2)I закон Кирхгофа

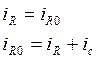
3)II закон Кирхгофа

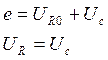
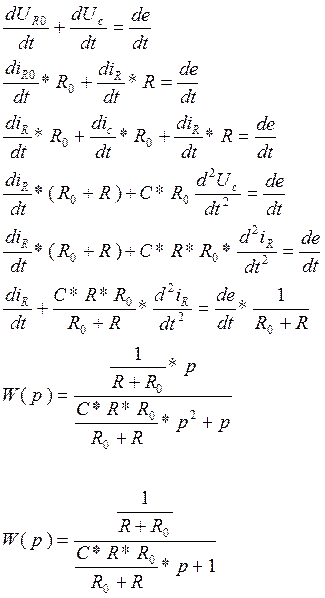
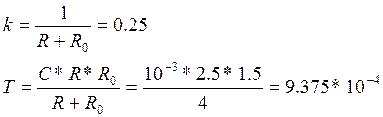
Пункт 2

Расчёт ЭДС двумя способами:

1 способ:

 

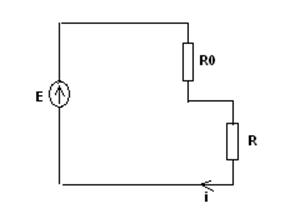
E=i*(R+R₀)=100*4=400 B

2 способ:

E(p)=i(p)/W(p)

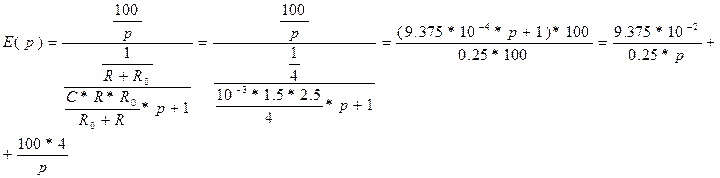
Пункт 3

Переходная характеристика  инерционного звена первого порядка:

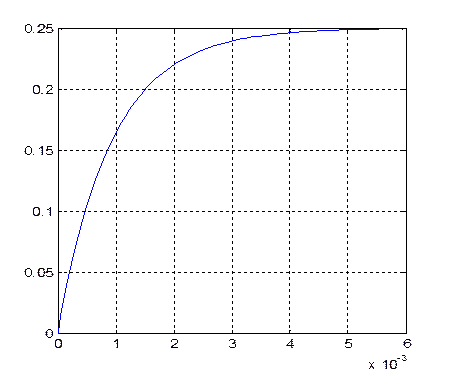
Это аналитическая переходная характеристика звена, эквивалентирующего нагрузку

Пункт 4

Имитационная модель для вычислительного комплекса РИТМ:

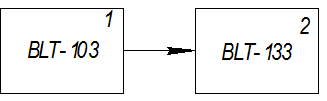
BLT-103-генератор кусочно-постоянного сигнала

BLT-133-инерционное звено первого порядка

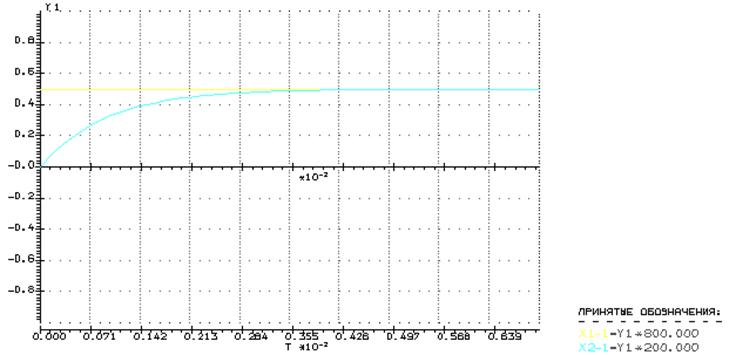
Экспериментальная переходная характеристика, полученная в вычислительном комплексе РИТМ:

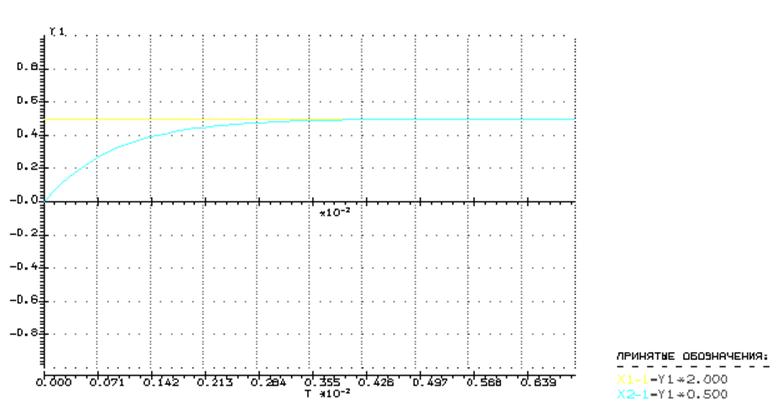
Экспериментальное определение параметров цепи T и k:

 

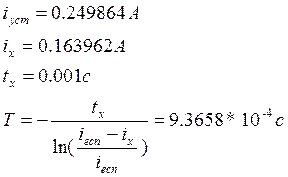
k=0.25 – установившееся значение

Точность расчета:

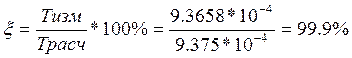
Пункт 5

            Для проверки правильности определения ЭДС, зададим входной сигнал, равный величине рассчитанной ЭДС. Таким образом, на выходе мы должны получить номинальный ток в установившемся режиме при правильном расчете. Схема имитационной модели осталась такая же.

 

            На вход подаем ЭДС Е=400 В, получаем ток i=100 А, что соответствует действительности.

Пункт 6

Для экспериментального определения АФЧХ нам потребуются семь значений . Для их определения воспользуемся расчетной АФЧХ инерционного звена 1-го порядка с нашими параметрами.

Для ее построения воспользуемся следующими формулами:

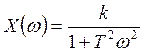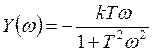;, где k=0.25, T=0.0009375

,

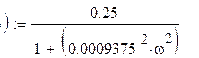
где X(ω), Y(ω) – соответственно вещественная и мнимая части функции W(jω).

Эта зависимость имеет вид:

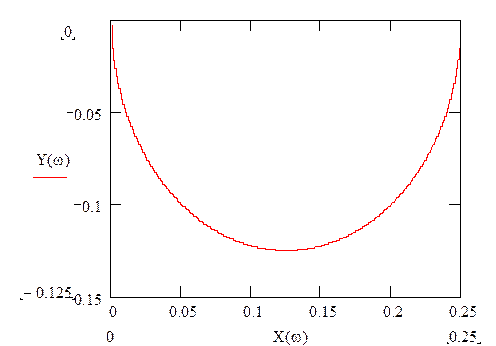
Воспользовавшись функцией трассировки данных, доступной в математическом пакете MathCAD 11, получим семь значений X(ω):

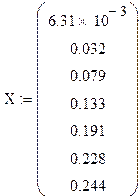
Выразив ω через X, найдем искомые семь значений ω для снятия экспериментальной АФЧХ.

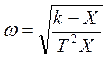
Проведя расчет в математическом пакете MATLAB 6.5, получим:

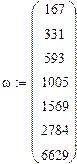
Для проверки подставим эти значения в выражения для X(ω) и Y(ω) и построим

полученную зависимость:

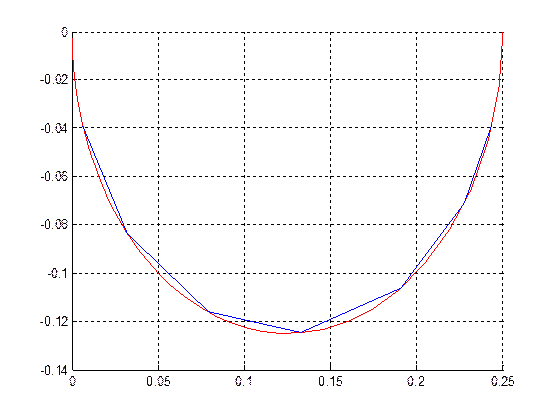Условные обозначения:

- аналитическая АФЧХ

 - проверочная АФЧХ

Таким образом, видно, что полученные значения ω истинны.

На основании этих данных заполним таблицу:

№ опыта	ω, рад/с	f, Гц	T, c	Tок, c	Тга, с	Xm	φ, рад	W'	W''
1	167,3	26,626622	0,037556	0,2253	0,1878	0,24698	-0,156	0,2440	-0,0383
2	331,3	52,728033	0,018965	0,1138	0,0948	0,23875	-0,301	0,2280	-0,0708
3	592,8	94,34705	0,010599	0,0636	0,0530	0,21851	-0,507	0,1910	-0,1062
4	1000,5	159,234521	0,006280	0,0377	0,0314	0,18233	-0,753	0,1330	-0,1247
5	1569,3	249,761852	0,004004	0,0240	0,0200	0,14054	-0,973	0,0791	-0,1162
6	2784,1	443,103277	0,002257	0,0135	0,0113	0,08944	-1,205	0,0320	-0,0835
7	6628,8	1055,006287	0,000948	0,0057	0,0047	0,03968	-1,41	0,0064	-0,0392

Помимо этих, есть еще две величины, не представленные в таблице по той причине, что они остаются одинаковыми для всех опытов. Эти величины:

1. τ – время окончания переходного процесса, с.

τ = 0.0009375 с

2. h – шаг расчета, с

h =  c

Пункт 7

Эти данные позволят нам смоделировать эксперимент по снятию АФЧХ инерционного звена 1-го порядка в вычислительном комплексе РИТМ. Сущность эксперимента состоит в том, что мы будем подавать на вход звена гармонический сигнал с разными частотами ω (см. таблицу), и нулевой начальной фазой. Регистрируя амплитуду выходного сигнала и разность фаз входного и выходного сигналов, мы получим данные, необходимые нам для построения экспериментальной АФЧХ.

      Схема имитационной модели имеет вид:

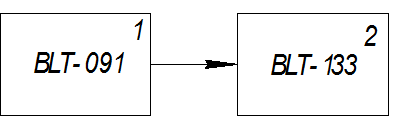
BLT-091-генератор гармонического сигнала

BLT-133-инерционное звено первого порядка

Вид входного и выходного сигналов для сдвига фаз

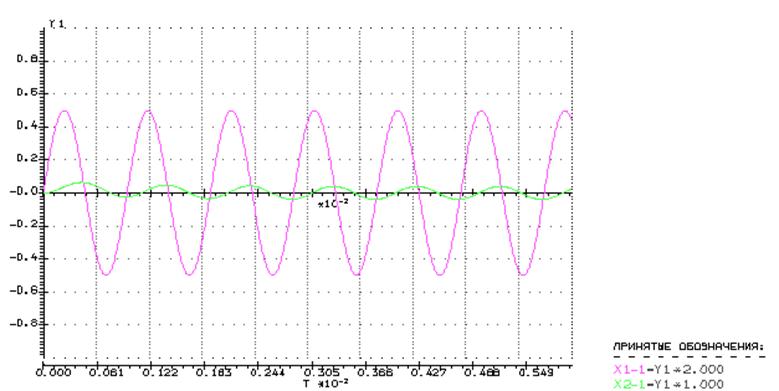
Результатами эксперимента являются данные в графах Xm и φ. Графы W’ и W’’ содержат информацию, являющуюся результатом обработки полученных данных. Используем их для построения экспериментальной АФЧХ:

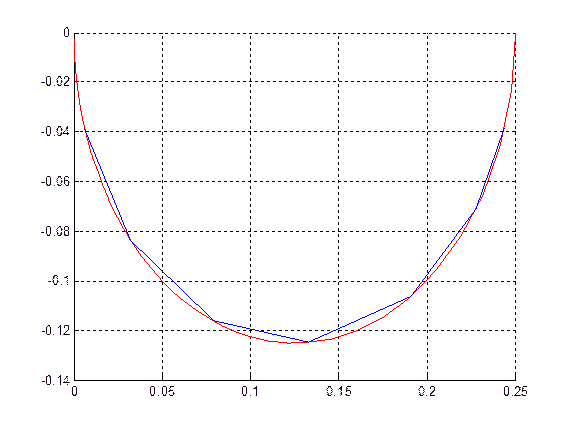
Условные обозначения:

- аналитическая АФЧХ

 - экспериментальная АФЧХ

Пункт 8

Составление структурной алгоритмической схемы системы автоматического управления.

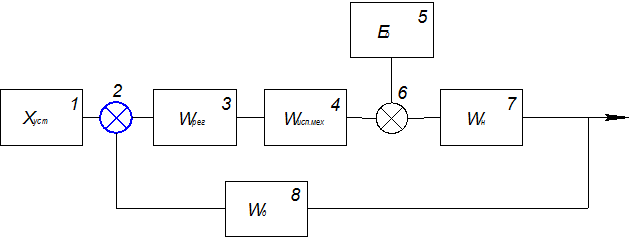
Эквивалентная схема:

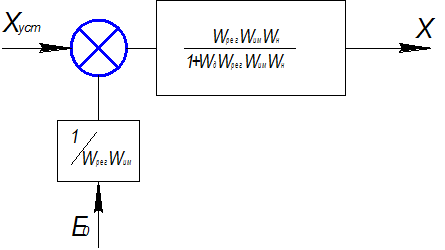
1)входной сигнал E₀

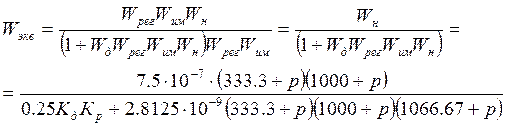
2)входной сигнал X_уст

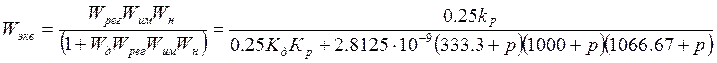
Из выражений видно, что, независимо от входного сигнала(E₀ ,X_уст), характеристический полином в знаменателе остаётся неизменным.

Пункт 9

Для определения границы устойчивости существует 3 математических условия:

-свободный член характеристического полинома равен нулю.

2)-коэффициент при старшей степени равен нулю.

3)-предпоследний определитель матрицы Гурвица равен нулю.

В нашем случае из этих трех условий мы можем реализовать только 1) и 3), т.к. а₀ не зависит от К_р и К_д.

Рассмотрим первое математическое условие:

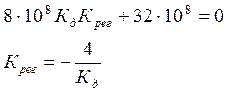
Рассмотрим второе математическое условие:

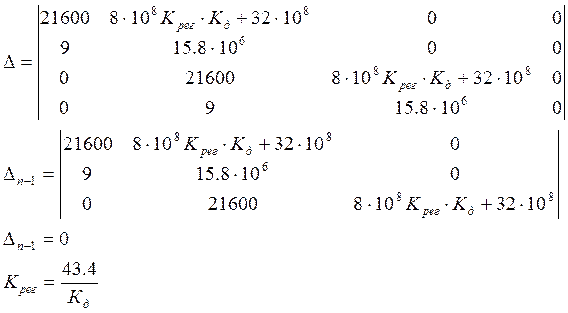
Область устойчивости

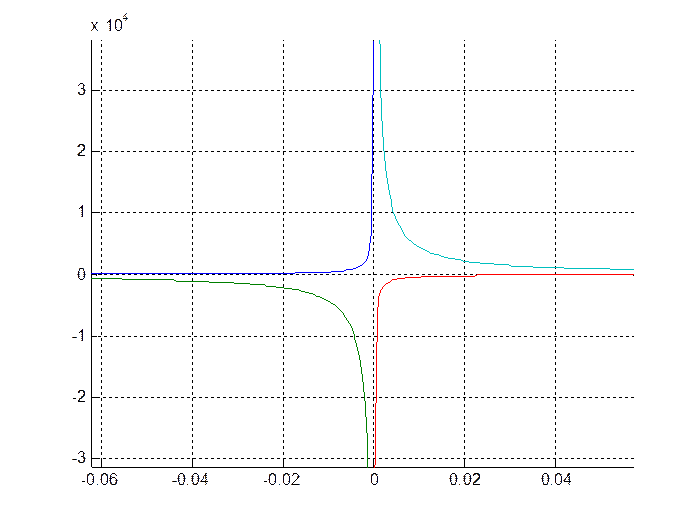
Пункт 10

По указанию преподавателя из области устойчивости мы выбрали

            Произведем проверку точки на устойчивость критерием устойчивости Гурвица.

Условия устойчивости:

Положительность определителя Гурвица и всех его диагональных миноров, т.е. должны выполняться следующие условия:

 

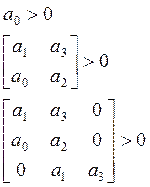
В нашем случае получили:

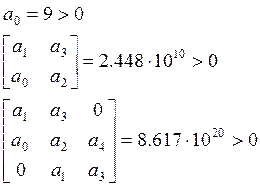
Таким образом, выполняются все условия устойчивости по Гурвицу, следовательно система при выбранных настройках будет работать устойчиво.

            Осциллограмма переходного процесса:

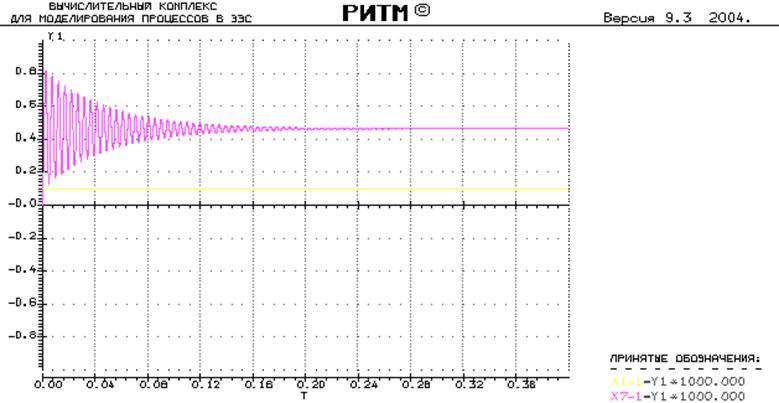
            Как видно из приведенной осциллограммы, система устойчива, но при номинальном значении ЭДС основного источника  на выходе звена нагрузки не обеспечивается номинальное значение выходной величины.

Это связано с тем, что сигнал, поступающий на сумматор проходит пропорциональное звено с коэффициентом  Это приводит к тому, что на регулятор и исполнительный механизм всегда поступает  разность сигналов уставки и нагрузки, что ведет к резкому увеличению сигнала на выходе нагрузки.

Эту проблему можно решить путем введения в схему последовательно с источником сигнала уставки такого же пропорционального звена.

Таким образом, нивелируется разность сигналов в установившемся режиме.

Пункт 11