Реализация схемных мероприятий по оптимизации системы и повышению ее точности в статических режимах, страница 2

Новая схема имитационной модели:

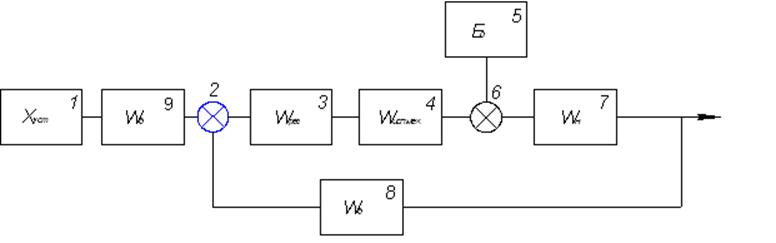
Переходный процесс принимает вид:

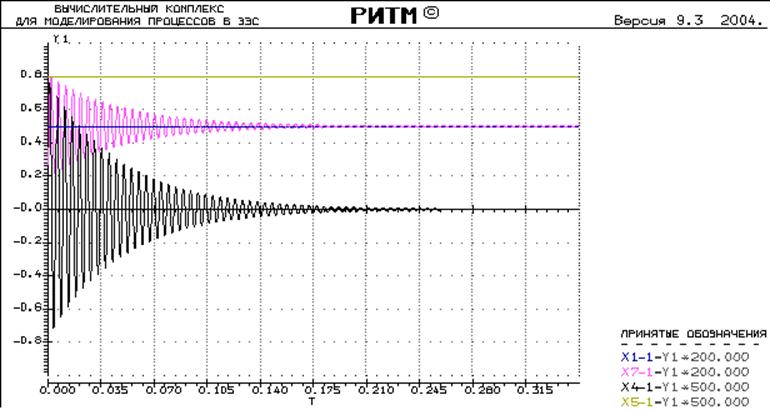
Как видно, теперь на выходе нагрузки обеспечивается номинальное значение выходной величины в 100 А в статическом режиме.

Теоретический расчет величины статизма и перерегулирования:

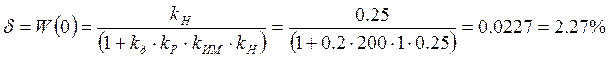
Для теоретического определения величины перерегулирования необходимо найти значения корней характеристического полинома при заданных значениях :

Корни:

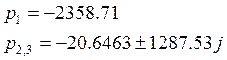
Отношение мнимой части корней к вещественной:

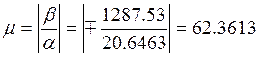
Формула для расчета теоретического перерегулирования:

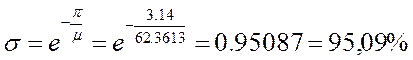
Проведем теперь обработку экспериментальных данных:

,

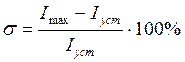=59.3%-перерегулирование

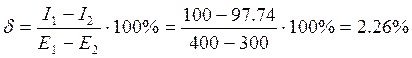-статизм

Как видно из полученных результатов, значение статизма, полученное теоретически и экспериментально, практически совпадают.

Пункт 12
Схема имитационной модели осталась прежней.

Осциллограмма процесса:

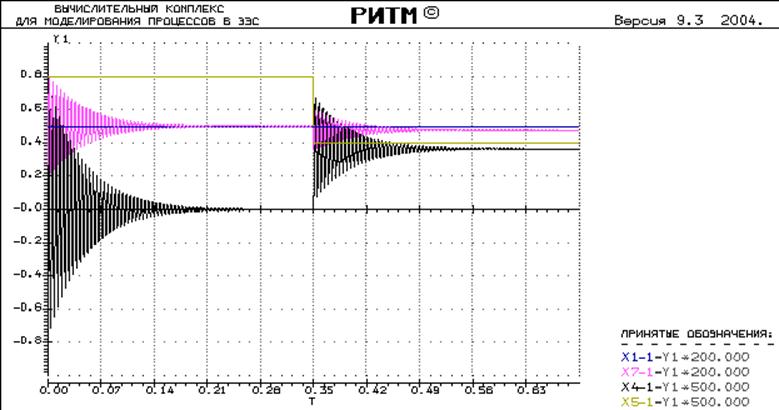
Авария происходит через 0.35 секунд после включения.

Необходимо обработать новые экспериментальные данные и определить новые значения статизма и перерегулирования и сравнить их со старыми:

,

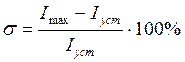=59.3%-перерегулирование

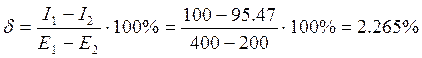-статизм

Как видно из приведенных выше результатов, значения совпадают.

Пункт 13

Как видно из результатов, только один из требуемых показателей системы соответствует требованиям (статизм <5%, перерегулирование <30%). Необходимо найти такую точку в области устойчивости, где бы обеспечивались оба требования.

Попробуем доказать экспериментально, что такой точки в области устойчивости нет. Для этого воспользуемся условием  и найдем границы области хорошего статизма в координатах Kр(Кд):

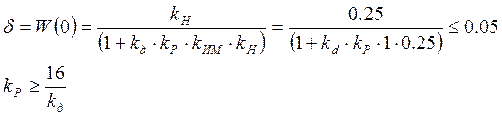
Решение этого уравнения дает нам область настроек, где статизм будет меньше 5%.

Построим эту область на области устойчивости:

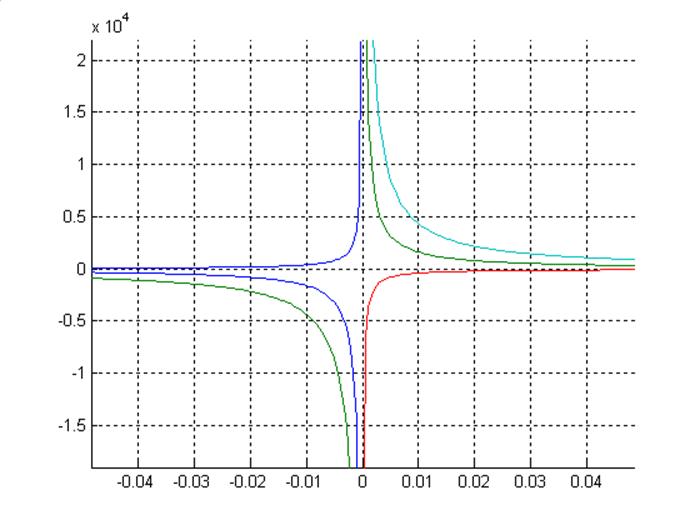
Полученная область устойчивости с хорошим статизмом находится в первом и третьем квадрантах между границами области хорошего статизма и границами области устойчивости.

Для дальнейшего доказательства проведем 3 одинаковых эксперимента с различными значениями коэффициентов Кр, Кд из разных областей.

1. Первую точку мы уже исследовали – это точка со значениями Кр=200, Кд=0.2

Значения статизма и перерегулирования для нее:

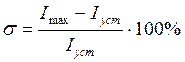=59.3%-перерегулирование

-статизм

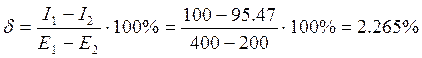2. Возьмем теперь точку на границе области с хорошим статизмом:

Значения коэффициентов: Кр=40, Кд=0.4

Экспериментальные данные:

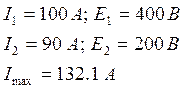
Значение статизма и перерегулирования в этой точке:

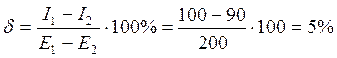
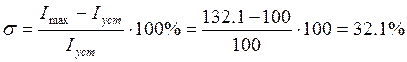
Как видно из результатов, на границе области с хорошим статизмом перерегулирование все равно превышает заданные требования.

3. Возьмем теперь точку вне области хорошего статизма:

Значения коэффициентов Кр=40, Кд=0.2

Экспериментальные данные:

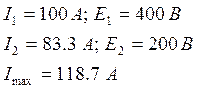
Значение статизма и перерегулирования в этой точке:

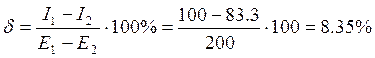
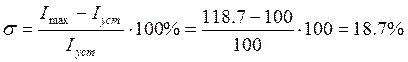
Таким образом, в этой точке обеспечивается хорошее значение перерегулирования, но статизм в этой точке не удовлетворяет тем требованиям, которые мы к нему предъявляем. Можно сделать вывод, что при удалении точки настроек от границ области устойчивости перерегулирование снижается, а статизм растет. Таким образом, считаем, что нет такой точки в области устойчивости, при выборе настроек в которой оба показателя системы были бы в пределах наложенных на них ограничений.

Несмотря на это, выберем точку 3 из области устойчивости, так как есть некоторые мероприятия, позволяющие улучшить статизм системы.

Пункт 14

            Для улучшения показателей системы, необходимо уменьшить статизм. Для этого воспользуемся методом астатического управления. Суть метода заключается во введении в слаботочную цепь схемы интегрирующего звена, причем таким образом, чтобы оно попало в глобальную обратную связь системы.

            При этом структурно-алгоритмическая схема примет следующий вид:

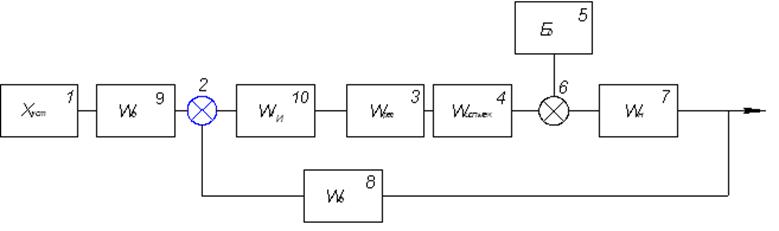
А передаточная функция системы будет равна:

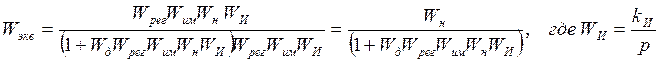
            Как видно из вышеприведенного выражения, подстановка значения р=0 даст в знаменателе бесконечность, и, соответственно,  . Так как добавление нового звена изменяет знаменатель передаточной функции, необходимо заново определить область устойчивости.

            Для этого зафиксируем значение коэффициента датчика Кд=0.2 и будем строить область устойчивости в координатах Ки(Кр).

            Передаточная функция имеет вид:

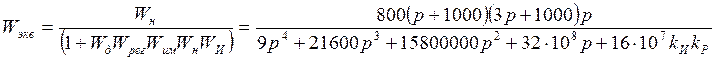
Знаменатель передаточной функции:      

Для определения границы устойчивости существует 3 математических условия:

-свободный член характеристического полинома должен быть больше или равен нулю, т.к все остальные больше нуля.

2)-коэффициент при старшей степени равен нулю.

3)-предпоследний определитель матрицы Гурвица равен нулю.

В нашем случае из этих трех условий мы можем реализовать только 1) и 3), т.к. а₀ не зависит от К_р и К_д.

1). Рассмотрим первое математическое условие:

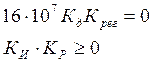
Получаем условие, что оба коэффициента должны быть одного знака, т.е. их значения должны находиться в 1-м или 3-м квадранте.

Рассмотрим второе математическое условие:

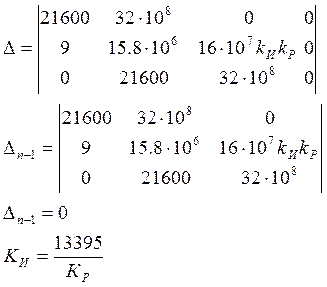
Получили второе уравнение для границ новой области устойчивости. Построим ее:

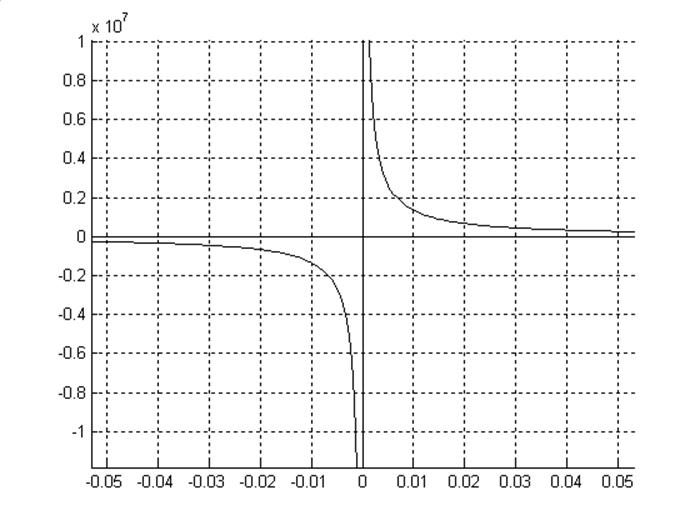
Выберем точку из этой области устойчивости:

Пусть Ки=200; Кр=40

Таким образом, получим значения коэффициентов системы:

 Ки=200; Кр=40;Кд=0.2

Проверим эту точку на устойчивость по Гурвицу.

            Необходимо выполнение следующих условий:

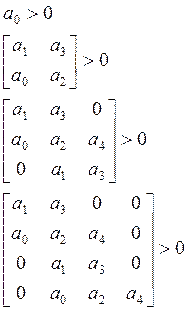
Получим:

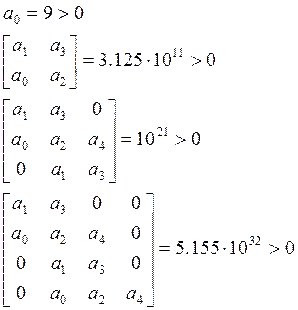
Таким образом, выполняются все условия устойчивости по Гурвицу, следовательно система при выбранных настройках будет работать устойчиво.

Получим осциллограмму процесса:         

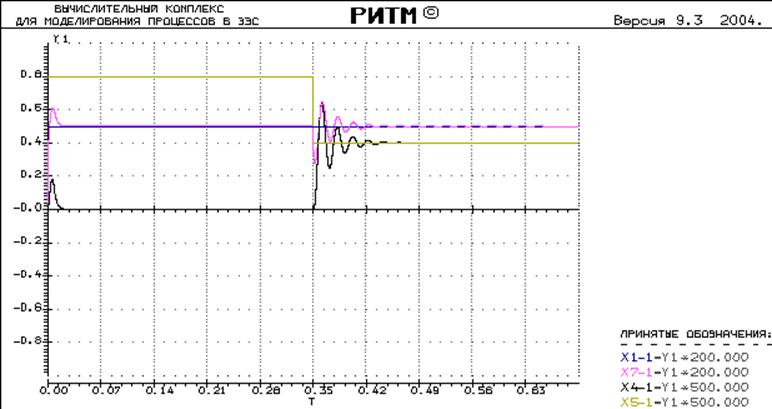
Обработка экспериментальных данных:

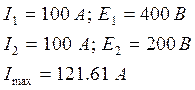
Значение статизма и перерегулирования в этой точке:

        

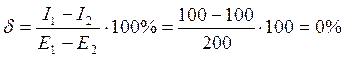
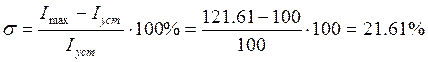
Мы реализовали принцип астатического управления и добились нулевого значения статизма и допустимого значения перерегулирования системы.

            Теперь необходимо оптимизировать систему по быстродействию. Для этого сначала подберем такие настройки, чтобы приблизительно уравнять и максимально возможно уменьшить время переходных процессов, проходящих при включении и аварии.

Таким образом, новые настройки системы:

Ки=55; Кр=40;Кд=0.2

Осциллограмма:

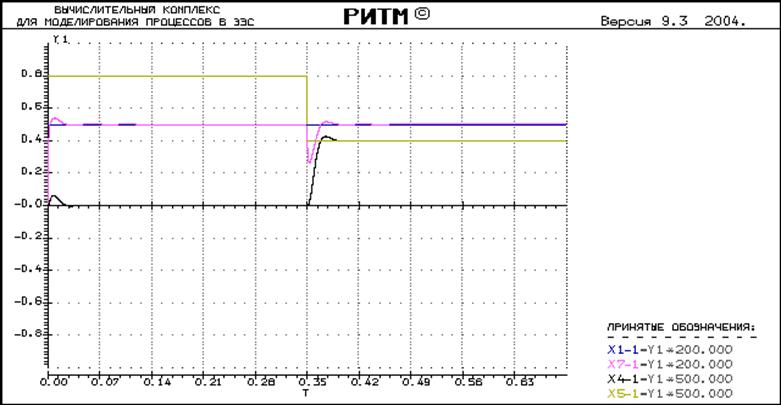
Время переходного процесса:

По заданию преподавателя необходимо еще уменьшить время переходного процесса. Для этого введем в слаботочную цепь пропорционально-дифференцирующее звено последовательно с самым медленным звеном схемы – исполнительным механизмом.

Уменьшение времени переходного процесса происходит за счет уменьшения постоянной времени самого медленного звена – исполнительного механизма. Передаточная функция этих двух звеньев, соединенных последовательно, равна:

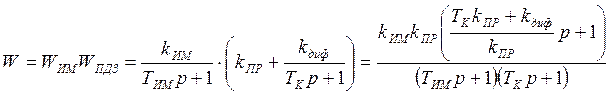
Таким образом, необходимо, чтобы 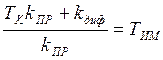 или, после преобразований:

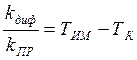
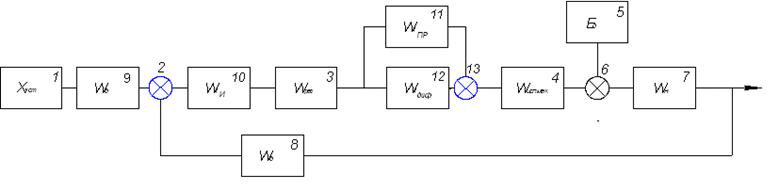
Схема имитационной модели примет вид:

Выбор коэффициентов ПДЗ:

Необходимо выбрать коэффициенты таким образом, чтобы постоянная времени T этих двух последовательно соединенных звеньев стала на порядок меньше, т.е.:

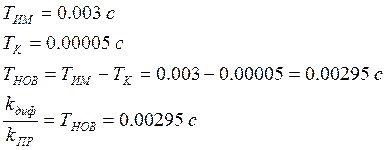
Отсюда подбираем отношение коэффициентов ПДЗ:

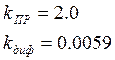
Получаем следующий вид переходного процесса:

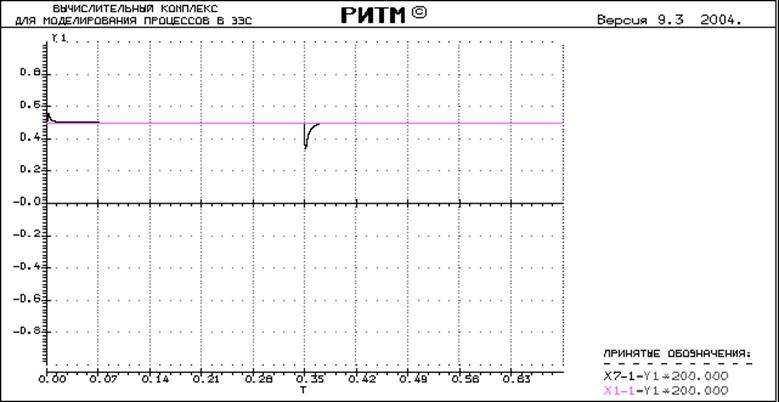
            Обработка экспериментальных данных:

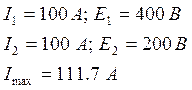
Значение статизма и перерегулирования в этой точке:

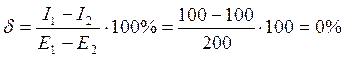
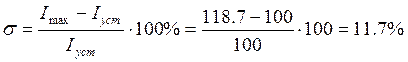
 - время переходного процесса

Таким образом, были реализованы схемные мероприятия по оптимизации системы и повышению ее точности в статических режимах. Нам удалось добиться требуемых значений статизма и перерегулирования и уменьшить время переходных процессов в системе при включении и аварии.