Пункт 8
Составить структурную алгоритмическую схему системы автоматического управления
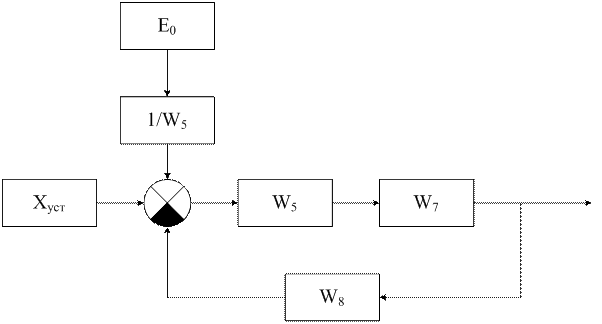
Исходная схема автоматического управления:
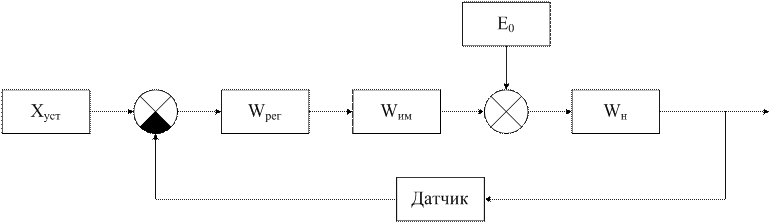
Для простоты преобразования присвоим номера отдельным блокам:
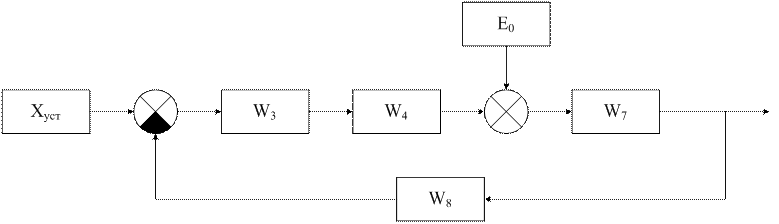
· Преобразования:
Звенья ![]() и
и ![]() объединим
в звено
объединим
в звено ![]() , как последовательно соединенные
звенья:
, как последовательно соединенные
звенья: ![]()
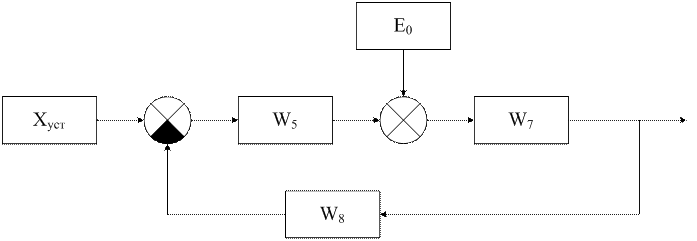
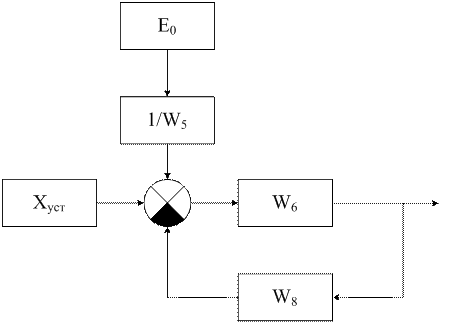
Переносим вперед через сумматор звено ![]()
Объединим сумматоры.
Звенья ![]() и
и ![]() объединим
в звено
объединим
в звено ![]() , как последовательно соединенные
звенья:
, как последовательно соединенные
звенья: ![]()
Звенья ![]() и
и ![]() объединим
в звено
объединим
в звено ![]() , как звено, охваченное обратной
отрицательной связью:
, как звено, охваченное обратной
отрицательной связью: 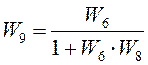
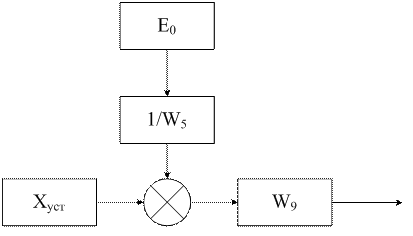
Так как у нас два интересующих сигнала, то рассмотрим схему с
сигналами ![]() и
и ![]() раздельно.
раздельно.
·
Рассмотрим относительно сигнала![]() :
:
Так как нас не интересует в этой части сигнал ![]() ,
то его можно не учитывать. Тогда схема примет следующий вид:
,
то его можно не учитывать. Тогда схема примет следующий вид:

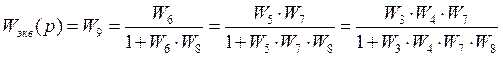
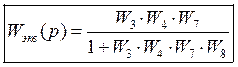
·
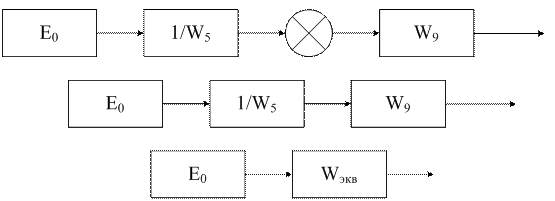
Рассмотрим относительно ![]() .
.
Поступим аналогично с сигналом ![]() как
с
как
с ![]() в прошлом пункте.
в прошлом пункте.
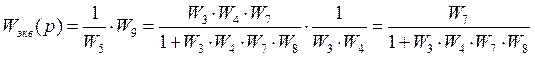
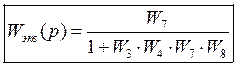
·
Подставим значения в ![]()
Для элементов цепи регулирования используются следующие эквиваленты: датчик, регулятор, исполнительный механизм.
Датчик – пропорциональное звено с коэффициентом ![]()
Регулятор – инерционное звено первого порядка с коэффициентом
усиления ![]()
![]() и
постоянной времени
и
постоянной времени ![]()
![]() .
.
Исполнительный механизм – инерционное звено первого порядка с
коэффициентом усиления ![]() и постоянной
времени
и постоянной
времени ![]()
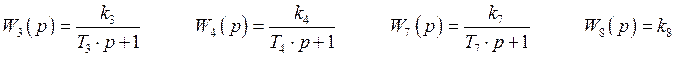
·
Для сигнала ![]()
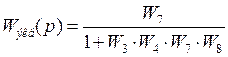
![]()
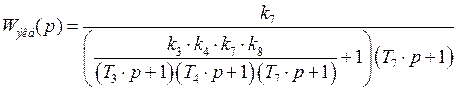
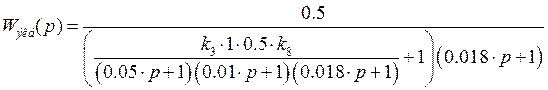
![]()
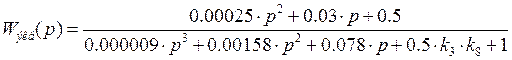
·
Для сигнала ![]()
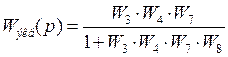
![]()
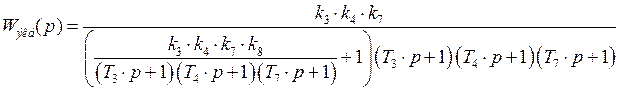
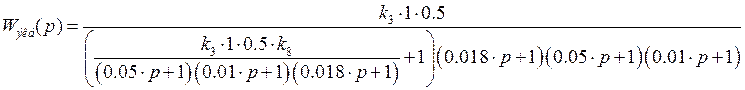
![]()
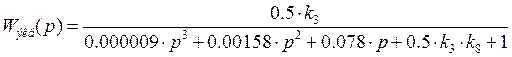
Пункт 9
Построить область устойчивости системы в плоскости коэффициентов Кр и Кд, где Кр – коэффициент передачи звена, эквивалентирующего регулятор, а Кд – коэффициент передачи звена, эквивалентирующего датчик текущего значения регулируемой переменной.
В прошлом пункте мы нашли ![]() с
одинаковым знаменателем:
с
одинаковым знаменателем:
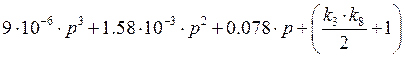
Получим характеристический полином, заменив ![]()
![]()
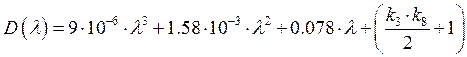
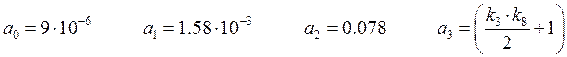
Для определения области устойчивости используем критерий Гурвица.
Условие устойчивости заключается в требовании положительности определителя Гурвица и всех его диагональных миноров.
Определитель Гурвица:
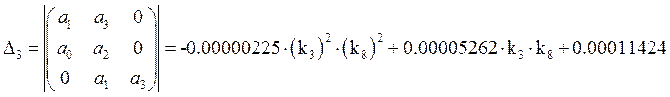
Найдем предпоследний минор:
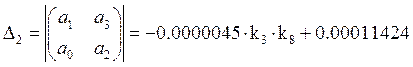
Для построения графика нужно решить два уравнения: ![]() и
и ![]()
·
![]()
![]()
![]()
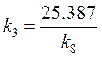
·
![]()
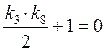
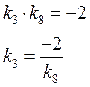
Построим график устойчивости:
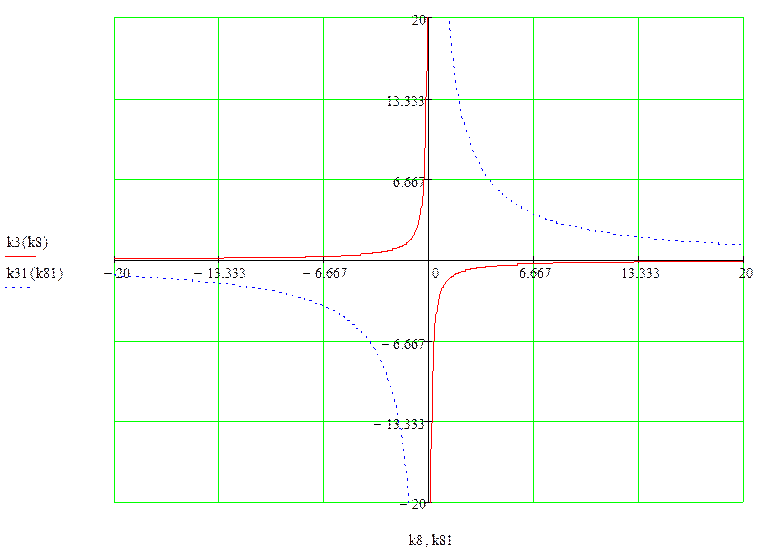
· Найдем области устойчивости:
Как видно по графику, мы получили 5 различных зон. Надо выбрать
зоны устойчивости, т.е. те зоны, точки которых соответствуют условию ![]() и
и ![]() .
.
Присвоим каждой зоне свой порядковый номер, и, взяв произвольные
точки, проверим выполнение условий ![]() и
и ![]() .
.
Зоны, в которых оба условия выполняются, являются искомыми. Если выполняется только одно условие, зона нам не подходит.
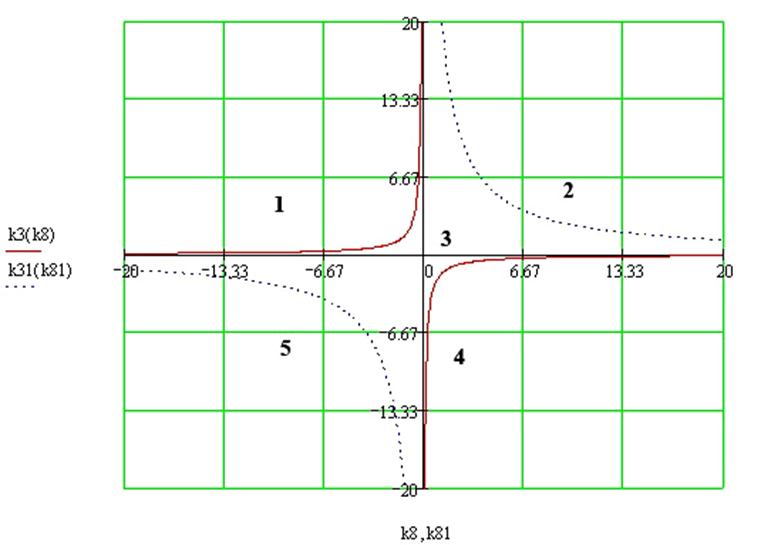
· Рассмотрим первую область.
Возьмем точку ![]() и
и ![]() :
:
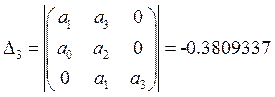
Не выполняется условие ![]()
· Рассмотрим вторую область.
Возьмем точку ![]() и
и ![]() :
:
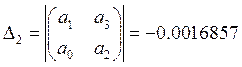
Не выполняется условие ![]()
· Рассмотрим третью область.
Возьмем точку ![]() и
и ![]() :
:
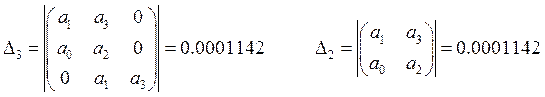
Оба условие выполняются, следовательно, это искомая область.
· Рассмотрим четвертую область.
Возьмем точку ![]() и
и ![]() :
:
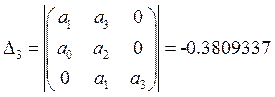
Не выполняется условие ![]()
· Рассмотрим пятую область.
Возьмем точку ![]() и
и ![]() :
:
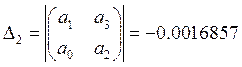
Не выполняется условие ![]()
Таким образом, после рассмотрения точек в пяти разных областях,
можно сказать, что областью устойчивости будет только третья, так как там
выполняются условия, о том что ![]() и
и ![]() .
.
Преподавателем было выбрано:
![]()
Пункт 10
Подготовить имитационную модель системы автоматического управления. Выполнить моделирование процесса включения системы питания при нулевых начальных условиях для заданных преподавателем величин коэффициентов Кр и Кд.
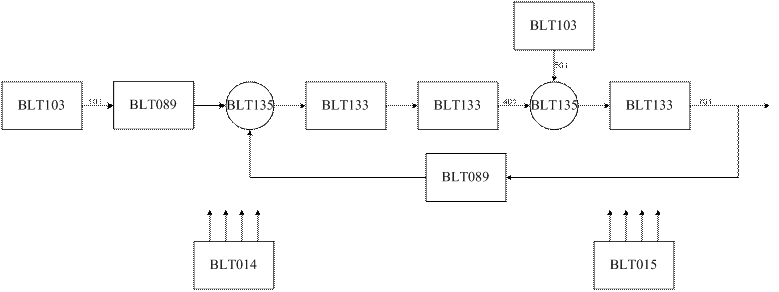
Наша модель имеет следующий вид:

В программе “Ритм” наша модель примет следующий вид:
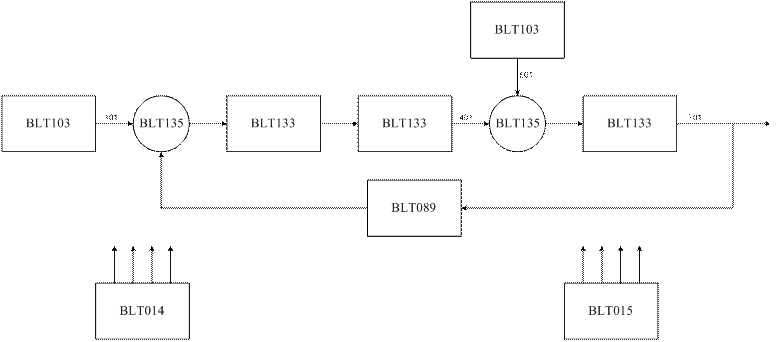
где:
BLT 103 – генератор кусочно-постоянного
сигнала (![]() и
и
![]() )
)
BLT 135 – сумматор
BLT 133 – инерционное звено I-ого порядка (регулятор, исполнительный механизм, нагрузка)
BLT 089 – пропорциональное звено (датчик)
BLT 014 – осциллограф
BLT 015 – табулятор
На осциллографе и табуляторе заданны четыре сигнала: выходной
(701), ![]() (501),
(501), ![]() (101)
и с исполнительного механизма (401).
(101)
и с исполнительного механизма (401).
На табуляторе все сигналы как дополнительные.
· Полученный результат:
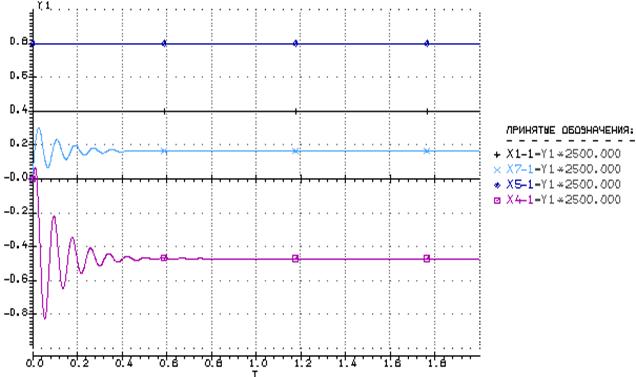
Пункт 11
Выбрать значения коэффициентов Кр и Кд из области устойчивости, которые в статическом режиме обеспечивают нулевую величину э.д.с. Ер регулируемого источника. По результатам эксперимента рассчитать статизм, перерегулирование и длительность переходного процесса для выбранных значений коэффициентов Кд и Кр. Рассчитать теоретические значения указанных показателей.
С осциллограммы в прошлом пункте видно, что сигнал ![]() в установившимся значение не равен
нулю. Следовательно, нам надо изменить точку настройки. А именно принять за
в установившимся значение не равен
нулю. Следовательно, нам надо изменить точку настройки. А именно принять за ![]() .
.
· Полученный результат:
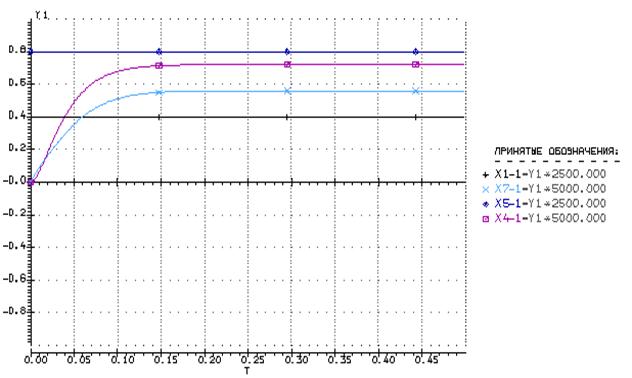
Нам пришлось увеличить максимум шкалы для сигнала 701 и 401. Видно,
что при данных настройках системы требуемое условие ![]() в
установившемся режиме не выполняется. Рассмотрим причины этой проблему.
в
установившемся режиме не выполняется. Рассмотрим причины этой проблему.
На сумматор 2 поступает сигнал 801:
![]()
но сигнал ![]() . Значит, в установившимся
режиме получаем:
. Значит, в установившимся
режиме получаем:
![]()
Это означает, что в установившимся режиме ![]() не
будет выполняться.
не
будет выполняться.
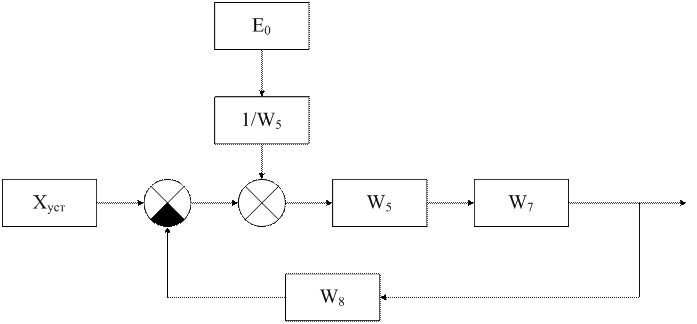
Для решения этой проблему добавим пропорциональное звено с передаточной функцией как у датчика. Т.о. мы изменим сигал 101, что бы получить:
![]()
Изменим нашу схему: добавим пропорциональное звено после ![]() и перед сумматором.
и перед сумматором.
· Проведем моделирование с новыми коэффициентами:
![]()
· Полученный результат:
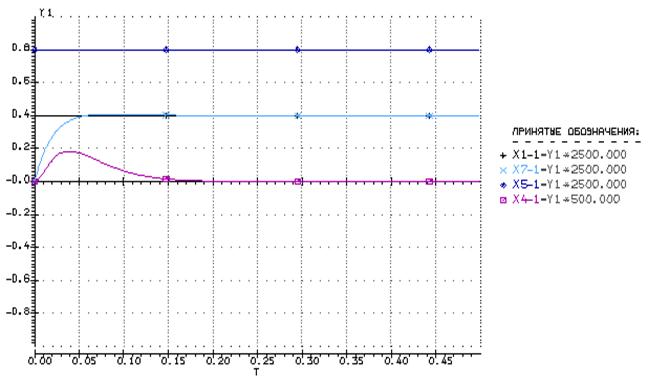
Рассчитаем опытные и теоретические значения статизма, перерегулирования и длительности переходного процесса.
· Расчет перерегулирования:
Опытное значение:
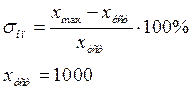
Из табулятора узнаем ![]() :
:

![]()
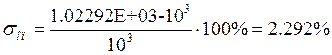
Теоретические:
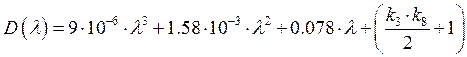
Корни характеристического полинома:
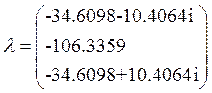
Определим колебательность переходного процесса, как отношение модулей мнимой и вещественной частей корней характеристического полинома.
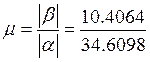
а перерегулирование:
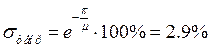
Вычислим погрешность:
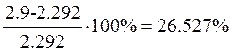
· Расчет длительности переходного процесса:
![]() Под длительностью переходного
процесса будем понимать время, которое прошло от начала процесса до момента,
когда исследуемая величина отличается от установившегося значения не более, чем
на 5%.
Под длительностью переходного
процесса будем понимать время, которое прошло от начала процесса до момента,
когда исследуемая величина отличается от установившегося значения не более, чем
на 5%.
Практические данные берем из табулятора:
![]()
Теоретические:
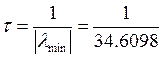
![]() Длительность переходного
процесса, определяющаяся затуханием экспоненциальной составляющей на 95 %
определяется как 3 постоянных времени
Длительность переходного
процесса, определяющаяся затуханием экспоненциальной составляющей на 95 %
определяется как 3 постоянных времени ![]() :
:
![]()
Определим погрешность:
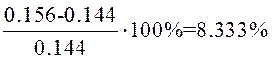
· Расчет статизма:
Для определения практического статизма изменим сигнал на входе после переходного процесса, и дождемся нового значения сигнала 701.
Подаем на вход ![]()
Из данных табулятора находим установившееся значение: ![]()
Далее подаем на вход ![]()
Из данных табулятора находим установившееся значение: ![]()
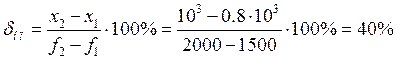
Теоретические:
Получаем теоретическое значение при подстановке p = 0 в передаточную функцию:
![]()
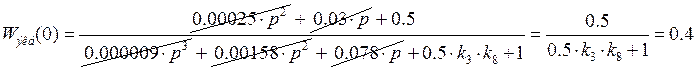
![]()
Пункт 12
Подготовить имитационную модель, позволяющую за один расчет выполнить:
моделирование процесса включения системы питания при нулевых начальных условиях с получением установившегося режима;
моделирование последующего переходного процесса, обусловленного потерей 50% величины э.д.с. Е0 с получением нового установившегося режима.
По результатам эксперимента определить статизм, перерегулирование и длительность протекания процесса. Сравнить с результатами выполнения п. 11.
Будем использовать модель из пункта 10, но с изменением в блоке 5
(генератор кусочно-постоянного сигнала ![]() ):
выставим момент изменения сигнала 0.5 с и новое значение сигнала 1000.
):
выставим момент изменения сигнала 0.5 с и новое значение сигнала 1000.
· Полученный результат:
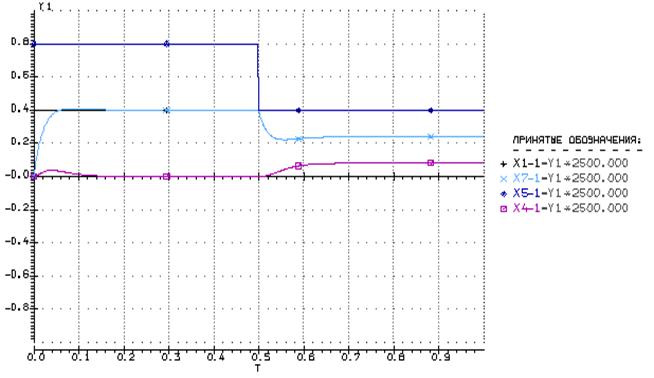
Определим показатели качества:
· Статизм
Из данных табулятора берем установившиеся значения:
![]()
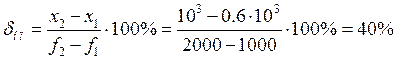
Теоретические:
Получаем теоретическое значение при подстановке p = 0 в передаточную функцию.
![]()
Но так как передаточная функция не изменилась, то статизм остался тот же что и в пункте 11.
![]()
· Перерегулирование
Опытное значение:
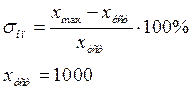
Из табулятора узнаем ![]() :
:

![]()
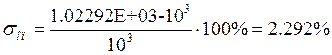
Теоретические:
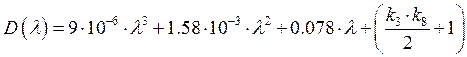
Корни характеристического полинома:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.