Информатика и выч. техника \ Теория автоматического регулирования

Составление структурной алгоритмической схемы системы автоматического управления. Построение области устойчивости системы в плоскости коэффициентов Кр и Кд, страница 2

Определим колебательность переходного процесса, как отношение модулей мнимой и вещественной частей корней характеристического полинома.

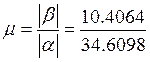
 а перерегулирование:

 

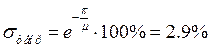
Вычислим погрешность:

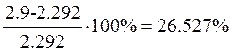
·  Расчет длительности переходного процесса:

Под длительностью переходного процесса будем понимать время, которое прошло от начала процесса до момента, когда исследуемая величина отличается от установившегося значения не более, чем на 5%.

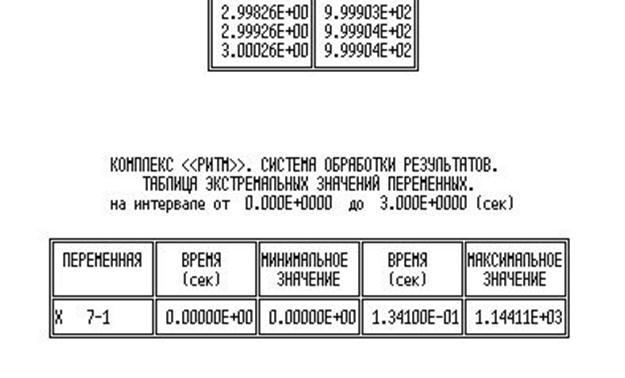
Практические данные берем из табулятора:

Теоретические:

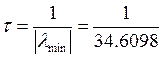
 Длительность переходного процесса, определяющаяся затуханием экспоненциальной составляющей на 95 % определяется как 3 постоянных времени :

Определим погрешность:

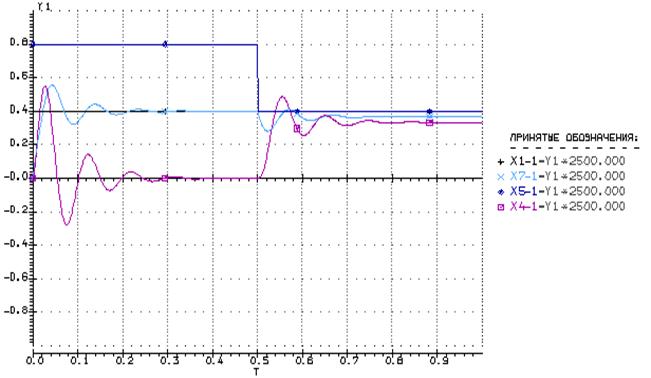
Показатели качества, как предполагалось, не изменились, что можно наблюдать и с осциллограммы.

Пункт 13

Задание:

Провести поэтапную оптимизацию коэффициентов Кр и Кд с целью обеспечения допустимых значений показателей качества.

Были установлены следующие задание: подобрать коэффициенты Кр и Кд такие, что бы выполнялось условие:

Или доказать что эти условия не выполнимы данной моделью.

·  Найдем коэффициенты для выполнения условия

Поскольку в доаварийном режиме нам необходимо, чтобы в установившемся режиме , то изменять параметр датчика мы не можем, Значит, необходимо изменять коэффициент регулятора. Т.о. фиксируем ,а значение  будем изменять в пределах области устойчивости.

Возьмем :

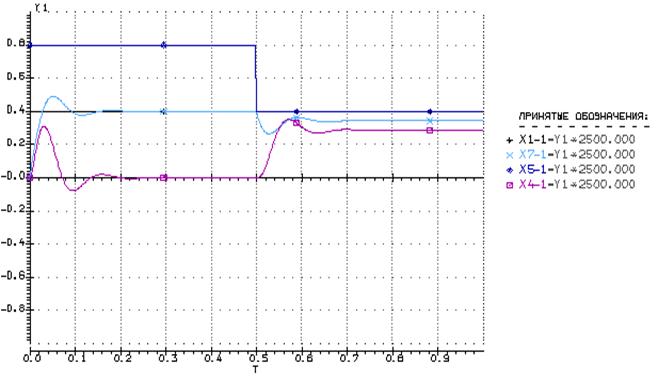
Рассчитаем статизм и перерегулирование:

·  Перерегулирование:

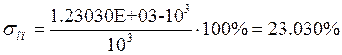
·  Статизм:

Из данных табулятора берем установившиеся значения:

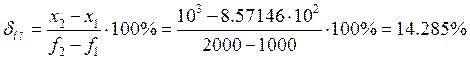
Возьмем :

Рассчитаем статизм и перерегулирование:

·  Перерегулирование:


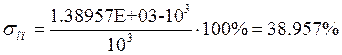
·  Статизм:

Из данных табулятора берем установившееся значение:

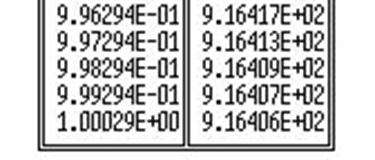
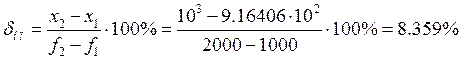
По полученным значениям можно сделать следующие выводы, что при уменьшении статизма возрастает перерегулирование. Следовательно, требуемых значений получить не возможно. Для подтверждения, такие коэффициенты датчика, при которых будет выполнятся .

·   Выполнение

Построим область с выполнением данного требования.

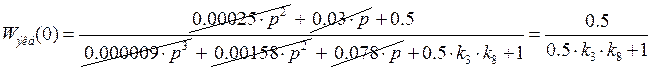
Нам надо добиться , следовательно :

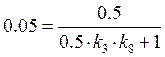
Считая, что :

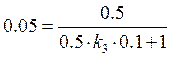
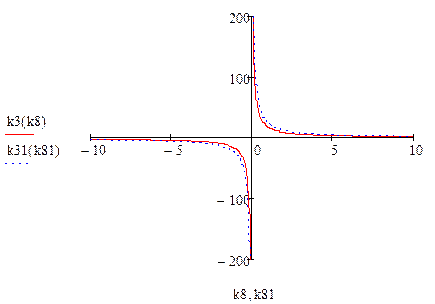
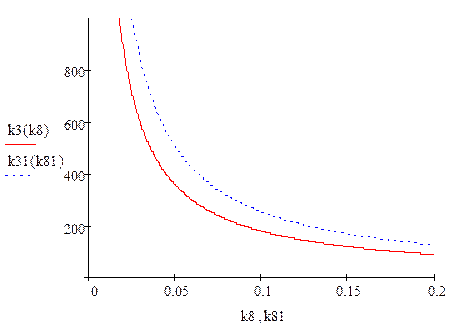
Построим график

 

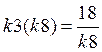
Как видно по графику, точки находящиеся между двумя графиками:

Возьмем :

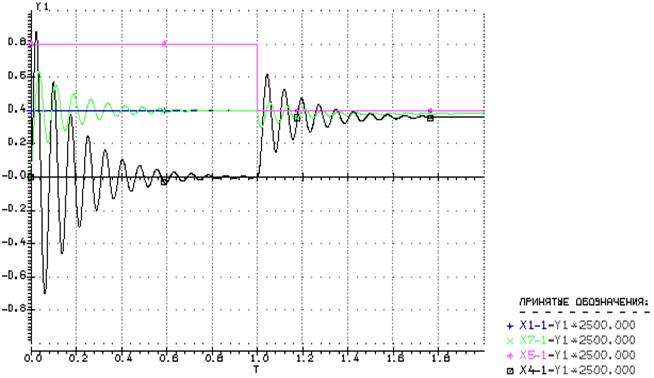
Данные из табулятора:

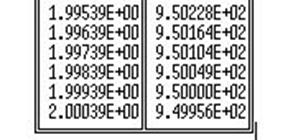
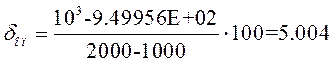
Требование выполнено. Точка настройки 

Рассчитаем перерегулирование


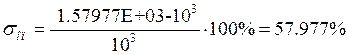
·  Выполнение :

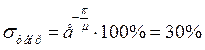
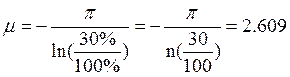
Подберем коэффициенты так, что бы их произведение было больше 2.609, т.е. .

Возьмем

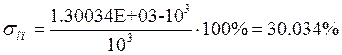
Требование выполняется. Точка настройки

Рассчитаем статизм для этой точки:

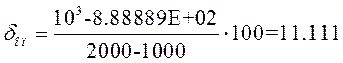
Для получения требуемого результата необходимо для фиксированного значения перерегулирования  уменьшать статизм. Это можно выполнить, осуществив астатическое управление. Нужно ввести в исходную схему САУ интегрирующее звено таким образом, чтобы в результате получения эквивалентной передаточной функции на предпоследней стадии преобразования это звено вошло в глобальную обратную связь.

Наша модель примет следующий вид:


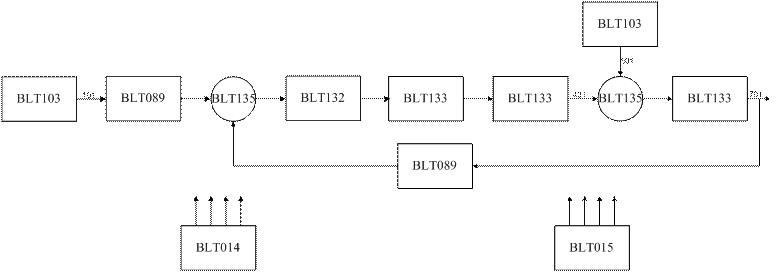
BLT 103 – генератор кусочно-постоянного сигнала ( и )

BLT 135 – сумматор

BLT 133 – инерционное звено I-ого порядка (регулятор, исполнительный механизм, нагрузка)

BLT 089 – пропорциональное звено (датчик)

BLT 014 – осциллограф

BLT 015 – табулятор

BLT 132 – интегрирующее звено

Так как мы изменили модель, то изменилась и эквивалентная передаточная функция, что могло изменить и область устойчивости. Построим заново область устойчивости относительно коэффициентов регулятора и интегрирующего звена().

Передаточная функция интегрирующего звена:

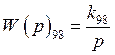
Эквивалентная передаточная функция приобретает вид:


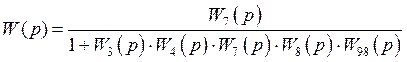
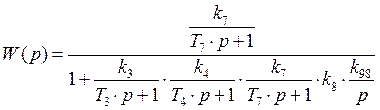
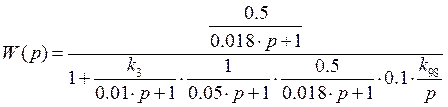
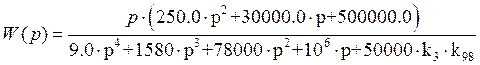
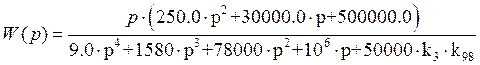
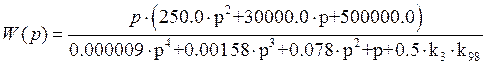
Для определения области устойчивости используем критерий Гурвица.

Условие устойчивости заключается в требовании положительности определителя Гурвица и всех его диагональных миноров.

  Определитель Гурвица:

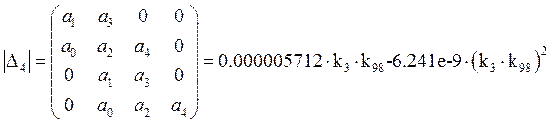
Найдем предпоследний минор:

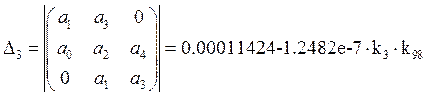
Для построения графика нужно решить два уравнения:  и

· 

· 

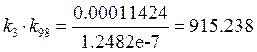
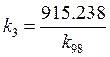
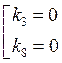
т.е. границами являются оси.

Поданным построим график трех функций:

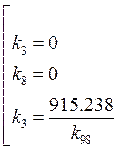
Полученный график:

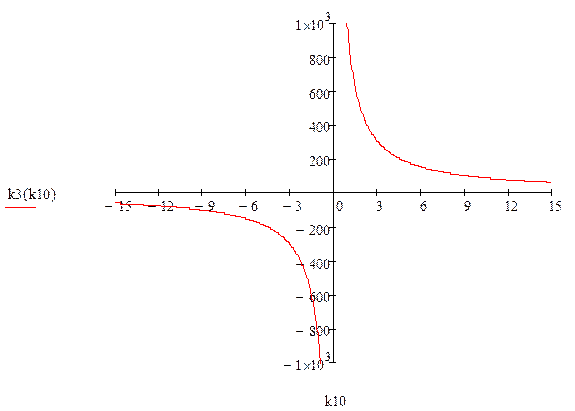
Разделим на области и найдем область устойчивости из условия  и .

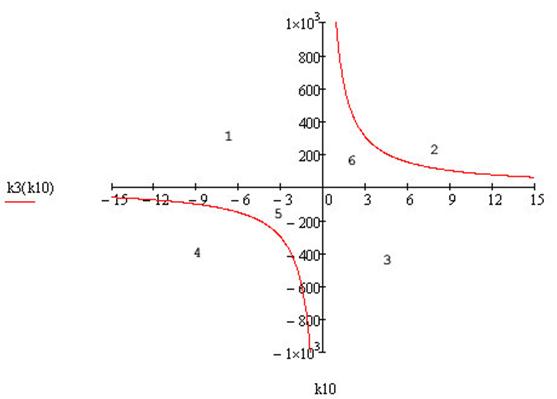
·  Рассмотрим первую область.

Возьмем точку и :

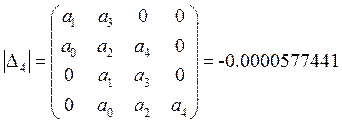
Не выполняется условие


·  Рассмотрим вторую область.

Возьмем точку и :

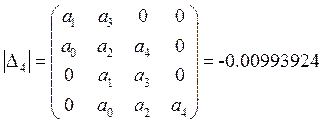
Не выполняется условие

·  Рассмотрим третью область.

Возьмем точку и :

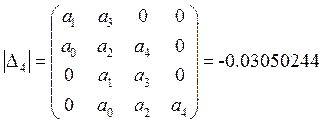
Не выполняется условие

·  Рассмотрим четвертую область.

Возьмем точку и :

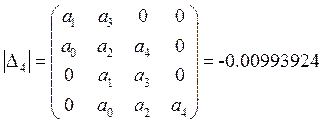
Не выполняется условие

·  Рассмотрим пятую область.

Возьмем точку и :

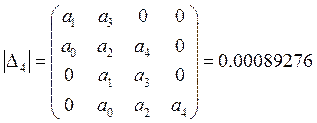
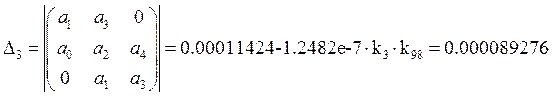
Т.е. это область устойчивости.


·  Рассмотрим шестую область.

Возьмем точку и :

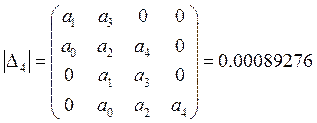
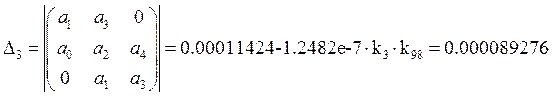
Т.е. это область устойчивости.

Исходя из проведенной проверки, получаем, что области, лежащие между осями координат и двумя гиперболами (область 5, область 6), является областями устойчивости.

Так как мы фиксировали значение перерегулирование, то  тогда:

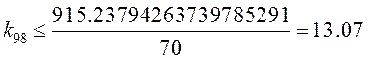
Возьмем :


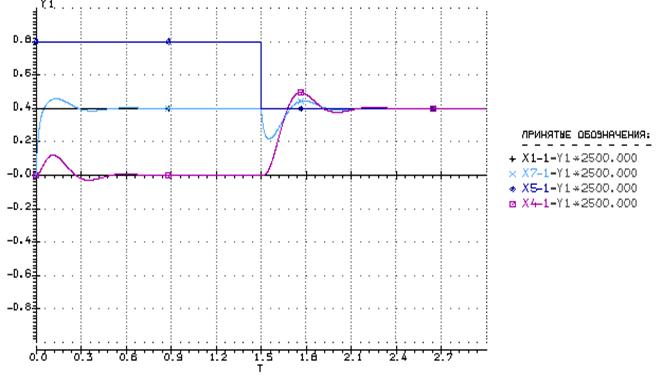
Рассчитаем показатели качества:

·  Статизм и перерегулирование:

Экспериментальные:

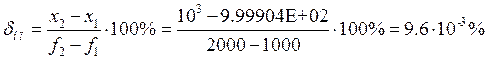
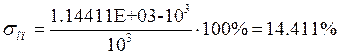
·  Длительность переходного процесса:

Экспериментальное:

t=0.64 c

Теоретическое:


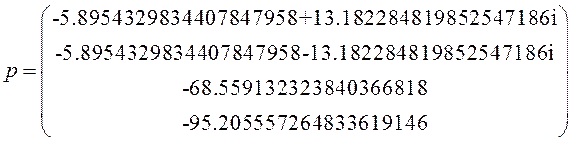
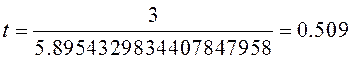
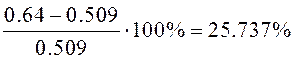
Подберем коэффициенты , так что бы получить минимальное время переходного процесса.

Возьмем

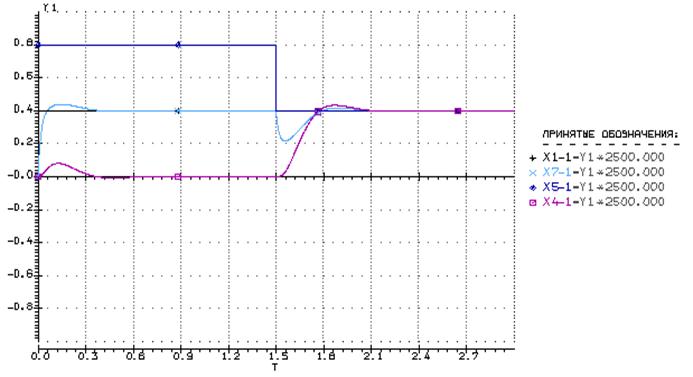
Рассчитаем показатели качества:

·  Статизм и перерегулирование, время переходного процесса:

Экспериментальные:

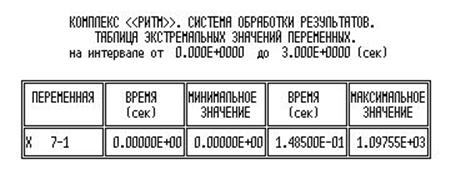
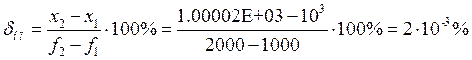
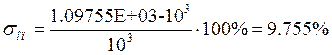
t=0.55 c


Теоретические:

·  Статизм:

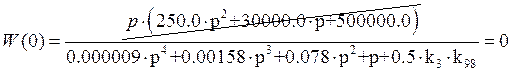
·  Перерегулирование:

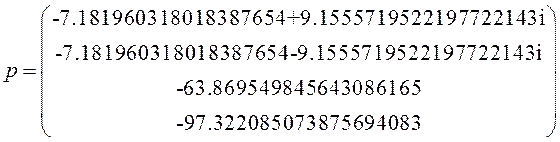
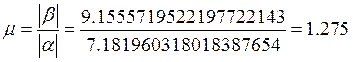
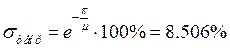
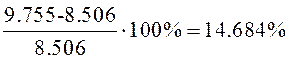
·  Длительность переходного процесса:

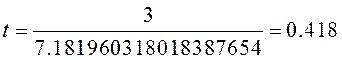
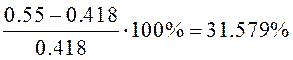
Все показатели попадают в допуск.

Пункт 14

Задание:

Предложить и реализовать схемные мероприятия, направленные на повышение точности системы в статических режимах и обеспечения требуемых показателей качества переходных процессов в соответствии с заданием преподавателя.

Необходимо увеличить быстродействие системы в два раза, не допуская при этом, чтобы напряжение на нагрузке превосходило двукратное значение ЭДС основного источника . Для увеличения быстродействия системы нужно скомпенсировать самую медленную составляющую. Самой медленной составляющей системы является постоянная времени исполнительного механизма с. Для ее компенсации воспользуемся корректирующим идеальным пропорционально-дифференцирующим звеном с особо подобранной передаточной функцией:

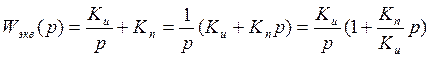
  Подбираем и так, чтобы .

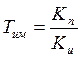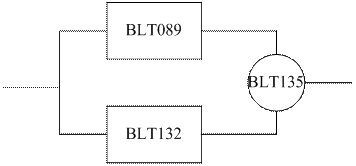
 Так как мы уже использовали идеальное интегрирующее звено в астатическом управлении, то можем ввести параллельно ему пропорциональное звено, чтобы получить в качестве корректирующего звена пропорционально-интегрирующее звено.

Тогда структурно-алгоритмическая схема нашей САУ примет следующий вид:

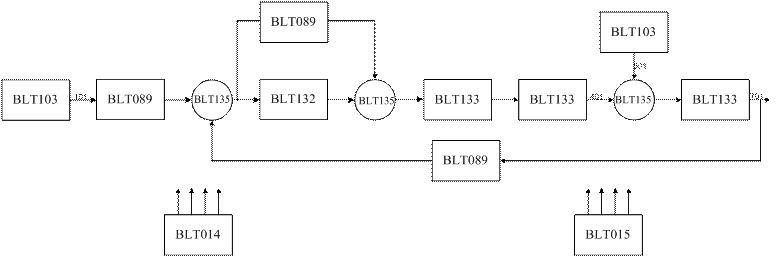
Рассчитаем показатели качества:

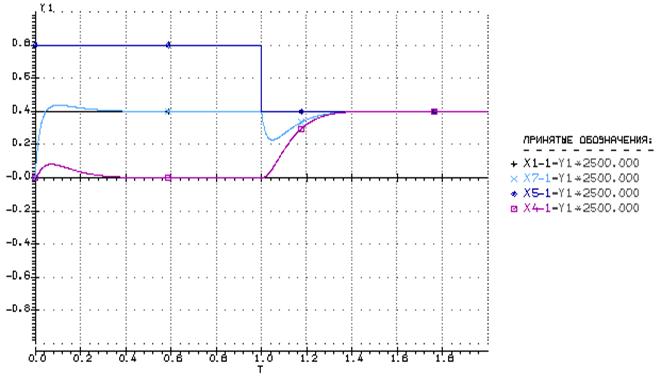
·  Статизм и перерегулирование, время переходного процесса:

Экспериментальные:

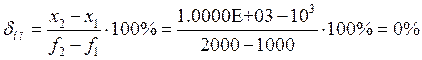
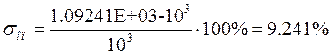
t=0.37 c


Теоретические:

·  Статизм:

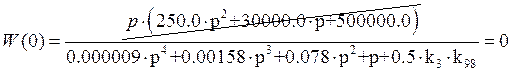
·  Перерегулирование:

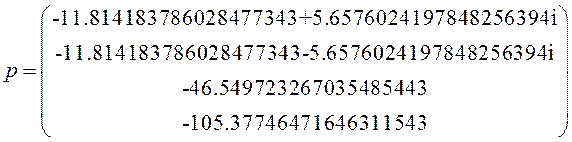
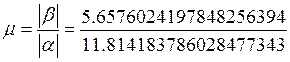
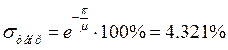
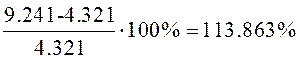
·  Длительность переходного процесса:

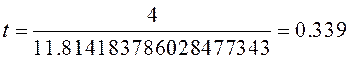
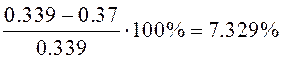
Все показатели попадают в допуск.

Максимальное значение напряжения:

 

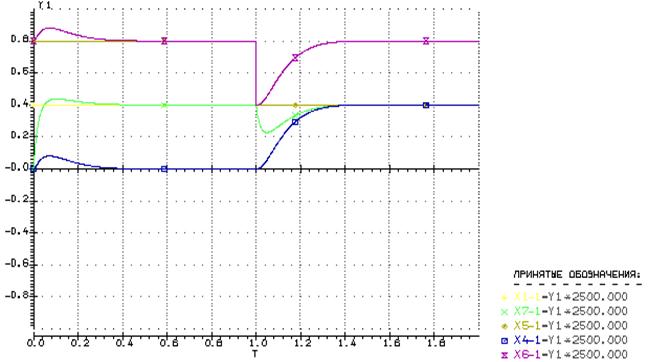
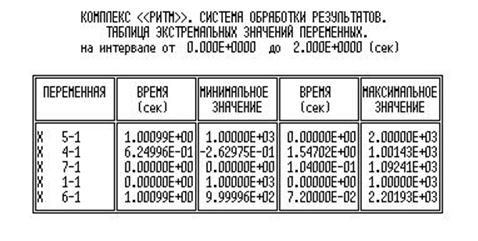
Напряжение на нагрузку, чуть больше чем основного источника. Все требования попадают в допуск.

·  Вывод:

в данной курсовой работе были исследованы системы электропитания и способы оптимизации параметров с целью повышения качества регулирования и улучшения характеристик переходных.

 В ходе работы мы разработали систему автоматического регулирования, позволяющую при аварии (потеря 50% ЭДС основного источника) свою работоспособность. Для улучшения показателей качества системы использовали астатическое управление и корректирующее звено. Из окончательного графика видно, что после проведения данных мероприятий  максимальное напряжение на нагрузке не превышает двукратного значения Е0, а значит изоляция нашей системы выдержит напряжение на нагрузке, таким образом проведенные мероприятия  привели к полной работоспособности нашей системы. Так же важно отметить, что цепь вышла слаботочной, что делает возможным применять её на практике.

Скачать файл