3.3. блочные коды
Блочным кодом ![]() называется
множество
называется
множество ![]() КК длиной
КК длиной ![]() символов,
каждой из которых однозначно соответствует информационное слово длиной
символов,
каждой из которых однозначно соответствует информационное слово длиной ![]() символов, причем хэмминговское
расстояние между любой парой КК не меньше
символов, причем хэмминговское
расстояние между любой парой КК не меньше ![]() .
.
Блочные коды строятся следующим образом: информационная
(кодируемая) последовательность символов разбивается на блоки из ![]() символов; каждому блоку символов
ставится в соответствие КК, представляющая собой набор из
символов; каждому блоку символов
ставится в соответствие КК, представляющая собой набор из ![]() символов (
символов (![]() ),
которая передается в канал связи. При блочном кодировании передаваемая КК
определяется только очередным передаваемым блоком информационных символов.
),
которая передается в канал связи. При блочном кодировании передаваемая КК
определяется только очередным передаваемым блоком информационных символов.
Примеры блочных кодов.
1. Табличные коды.
Табличные коды являются нелинейными кодами и строятся путем
эвристического (псевдослучайного) выбора ![]() КК из
множества
КК из
множества ![]() всех возможных слов длиной
всех возможных слов длиной ![]() символов, отличающихся друг от друга не
менее, чем в разрядах, причем каждой выбранной КК соответствует информационное
слово длиной
символов, отличающихся друг от друга не
менее, чем в разрядах, причем каждой выбранной КК соответствует информационное
слово длиной ![]() символов.
символов.
На передающей и приемной стороне в виде таблицы хранится соответствие КК информационным словам. Периодическая смена таблицы соответствия обеспечивает повышение информационной скрытности системы.
При ![]() ,
, ![]() и
и ![]() таблица кодирования выглядит следующим образом
(вариант).
таблица кодирования выглядит следующим образом
(вариант).
|
Информ. слова |
КК |
|
00 |
10001 |
|
01 |
00100 |
|
10 |
11110 |
|
11 |
01011 |
Для табличного кода с такими кодовыми словами может быть
построено ![]() таблицы соответствия. Очевидно, что
использование табличных кодов с большими
таблицы соответствия. Очевидно, что
использование табличных кодов с большими ![]() ограничено
сложностью аппаратурной реализации
ограничено
сложностью аппаратурной реализации
2. Коды с проверкой на четность (нечетность) ![]()
КК в подобных кодах содержат 1 проверочный разряд,
представляющий сумму по ![]() всех информационных
разрядов. Кодовое расстояние при этом равно 2.
всех информационных
разрядов. Кодовое расстояние при этом равно 2.
В кодах с проверкой на четность проверочный разряд выбирается таким, чтобы общее число символов «1» в КК было четным. В кодах с проверкой на нечетность проверочный символ обеспечивает нечетное число символов «1» в каждой КК.
Ниже показана
структурная схемы кодера для данного кода
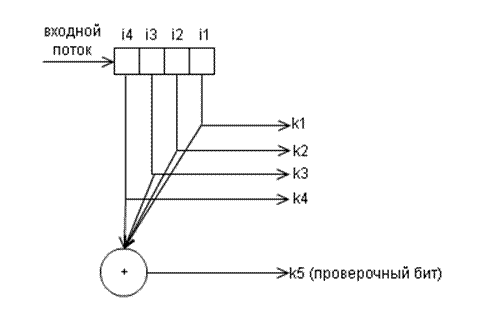
и и декодера
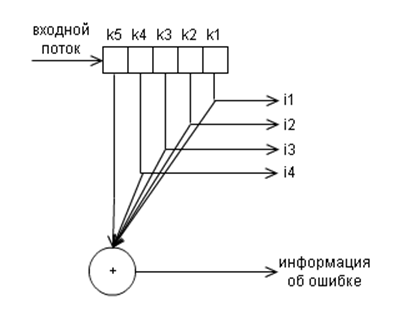
Подобные коды обеспечивают обнаружение однократной, а также любого нечетного числа ошибок в сообщении. Простота реализации и высокая относительная скорость этих кодов обеспечивает их широкое применение в системах управления и связи.
3. Коды с многократным повторением ![]()
КК в таких кодах содержат один информационный символ, повторяющийся
![]() раз, причем
раз, причем ![]() , как правило, нечетно. Кодовое
расстояние равно
, как правило, нечетно. Кодовое
расстояние равно ![]() , а относительная
скорость -
, а относительная
скорость - ![]() . Низкая
относительная скорость компенсируется хорошими корректирующими возможностями и
простотой реализации декодера с мажоритарной обработкой кодового слова.
. Низкая
относительная скорость компенсируется хорошими корректирующими возможностями и
простотой реализации декодера с мажоритарной обработкой кодового слова.
4. Коды Хэмминга
Двоичными кодами Хэмминга называют блоковые коды с кодовым
расстоянием ![]() , в которых
величины
, в которых
величины ![]() и
и![]() определяются следующими соотношениями:
определяются следующими соотношениями:
![]() , (1)
, (1)
где ![]() число проверочных
символов;
число проверочных
символов;
![]() число возможных событий (
число возможных событий (![]() соответствует приему КК без ошибок,
соответствует приему КК без ошибок, ![]() ошибка в
ошибка в ![]() символе).
символе).
Минимальная длина КК соответствует равенству в (1):
![]() или
или ![]() , что
соответствует коду
, что
соответствует коду ![]() .
.
Число проверочных разрядов ![]() ,
соответственно, кодами Хэмминга являются коды
,
соответственно, кодами Хэмминга являются коды ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и др.
и др.
В качестве примера рассмотрим процессы кодирования и декодирования линейных блочных кодов.
Можно показать, что линейный блочный код ![]() можно получить из
можно получить из ![]() линейно независимых КК путем их
поразрядного суммирования по
линейно независимых КК путем их
поразрядного суммирования по ![]() .
.
Исходные линейно независимые КК называются базисными.
Они могут быть объединены в виде матрицы размером ![]()
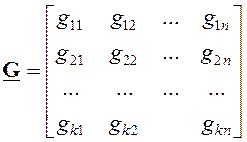 , которая называется порождающей.
, которая называется порождающей.
Тогда процесс кодирования может быть записан в виде матричного уравнения
![]() , где
, где ![]() вектор из
вектор из ![]() элементов, который соответствует
передаваемому информационному слову;
элементов, который соответствует
передаваемому информационному слову; ![]() вектор размером
вектор размером ![]() , соответствующий КК.
, соответствующий КК.
Таким образом, порождающая матрица содержит всю информацию
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.