Оптимальные методы приема радиосигналов

2.1.    ОПТИМАЛЬНЫЕ МЕТОДЫ ПРИЕМА РАДИОСИГНАЛОВ

Литература:

1. Теория электрической связи: Учеб. /Под ред. Д.Д. Кловского. - М.: Радио и связь, 1999. - С.165-192.

Оптимальными называют методы приема, которые в соответствии с выбранным критерием обеспечивают наилучший прием сигналов или переносимых ими сообщений при наличии помех.

Одним из основных допущений теории оптимальных методов приема является предположение о том, что заранее известны (или заданы) вид модуляции и класс используемых сигналов. При этом следует отметить, что одно и то же сообщение может быть передано различными радиосигналами.

Предметом теории оптимального приема радиосигналов является рассмотрение следующих вопросов:

-  обоснование выбора критерия оптимальности;

-  разработка теоретических методов отыскания структуры приемника, оптимального по выбранному критерию;

-  исследование свойств оптимальных приемников и определение минимального значения отношения сигнал/помеха, при котором достигается заданное качество воспроизведения сообщения (так называемая оценка помехоустойчивости приемника);

-  сравнение характеристик оптимальных приемников с реально используемыми для оценки целесообразности оптимизации приемников;

-  сравнение помехоустойчивости оптимальных приемников для различных видов радиосигналов с целью выбора более помехоустойчивых сигналов.

При определении структуры оптимального приемника наиболее важное значение приобретают следующие факторы: решаемая приемником задача, выбранный критерий оптимальности, вид передаваемого сообщения, вид используемых сигналов и объем априорных (т.е. заранее известных) данных о принимаемых сигналах, особенности соответствующих помех и специфика их воздействия на сигналы.

В РСПИ оптимальные приемники используются для решения следующих основных задач.

1. Обнаружение сигнала. Пусть в течение времени Т_н наблюдается входное напряжение приемника, которое может являться функцией сигнала и помехи. Следует оптимальным образом ответить на вопрос: присутствует или отсутствует сигнал на данном интервале наблюдения?

2. Различение (распознавание) нескольких сигналов. На входе приемника имеются один из М возможных сигналов и помеха. По реализации входного напряжения приемника на интервале Т_н требуется оптимальным образом решить, какой именно сигнал присутствует.

Обнаружение является частным случаем различения двух сигналов, один из которых равен нулю на всем интервале наблюдения.

3. Оценка параметров сигнала. По реализации входного напряжения приемника следует определить значение одного или нескольких параметров сигнала (амплитуды, частоты, фазы и т. д.), которые считаются на интервале Т_н неизменными. При этом сначала необходимо обнаружить сигнал, а затем измерять его параметры. Для каждой из этих операций нужен отдельный оптимальный приемник. Однако исследования [   ] показывают, что при определенных условиях (помеха представляет собой белый шум, аддитивно складывающийся с сигналом; отношение сигнал/шум достаточно велико) один и тот же приемник может быть с успехом использован как для обнаружения сигналов, так и для измерения их параметров. При этом характеристики приемника будут оптимальными (или очень близки к ним) для обеих операций.

4. Оценка процессов (фильтрация). Оценкой процессов называется воспроизведение сигналов или сообщений, представляющих собой случайные функции времени (например, человеческой речи, телевизионного изображения и т.п.), существенно изменяющиеся на интервале Т_н. При решении указанных задач необходимо по реализации входного напряжения приемника решить оптимальным образом, какая именно реализация полезного случайного процесса имеет место, т. е. какое сообщение присутствует в принятом колебании.

Приемник, решающий одну из перечисленных выше задач, описывается законом, по которому поступивший на его вход сигнал преобразуется в выходной информационный параметр (решение о наличии или отсутствии сигнала, решение о присутствии одного сигнала из нескольких возможных и т.п.). Этот закон называется правилом решения, а устройство, реализующее его, - решающим устройством (РУ).

2.1.1 Критерии оптимальности

При восстановлении сообщения l(t) по сигналу s_i(t), принятому с искажениями и помехами, можно судить только о вероятности того, что был передан тот или иной сигнал из множества возможных S= {s₀(t), s₁(t), ..., s_M-1(t)}. Вероятностный характер наблюдаемой смеси x(t) сигнала и помех приводит к тому, что любой приемник, как бы тщательно он не был спроектирован, время от времени выносит решения, не соответствующие действительности, считая, что в наблюдаемой смеси x(t) присутствует k-й сигнал s_k(t), тогда как в действительности в смеси содержится i-й сигнал s_i(t).

Рассмотрим задачу различения М детерминированных сигналов s₀(t), s₁(t), ..., s_M-1(t) на фоне помех с полностью заданным статистическим описанием, т. е. с точно известной плотностью вероятности (ПВ). В рамках такой модели различения ПВ наблюдаемого колебания x(t) при условии, что в x(t) входит сигнал с номером i, - некоторая вполне определенная функция, вид которой зависит лишь от номера i.

Предположим, что известна вероятность р_i присутствия в x(t) сигнала s_i(t). Эту вероятность называют априорной (доопытной), поскольку она отражает сведения, которыми располагает наблюдатель, еще не имея в распоряжении реализации x(t), и показывает, насколько часто при длительной эксплуатации данной РСПИ можно ожидать появления s_i(t) в x(t). Очевидно, вероятность р_i можно назвать и априорной вероятностью истинности гипотезы H_i о наличии i-го сигнала в смеси x(t), записав р_i= =P(H_i). Ясно также, что р_i подчинены условию нормировки 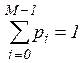, ибо гипотезы H₀, H₁, ..., H_M-1 составляют полную группу несовместных гипотез.

Предположим, что р_ik = P(|) - условная вероятность перепутывания i-го сигнала с k-м, т. е. принятия решения  (о присутствии s_k(t) в x(t)) при условии, что истинна  (в x(t) содержится s_i(t)). Следовательно, множество вероятностей р_ik при  составляет набор условных вероятностей всех ошибочных решений. Эти вероятности для любого фиксированного способа различения сигналов можно вычислить, так как помехи считаются полностью статистически заданными.