Оптимальные методы приема радиосигналов, страница 2

Введем М² неотрицательных величин П_ik, каждая из которых характеризует риск (потери, ущерб) от перепутывания i-го  сигнала с k-м. При этом правильные решения считаются не наносящими ущерба, так что П_ii = 0.

В каждой отдельной попытке различения сигналов итог (решение) оказывается случайным событием, а поэтому случайным будет и значение риска. Очевидно, безусловную вероятность того, что риск окажется равным П_ik, по теореме умножения вероятностей можно найти как P(H_i)P(|)= p_ip_ik, поэтому математическое ожидание риска (средний риск)

.                                                                                                                     (2.1)

Критерий минимального среднего риска (называемый также критерием Байеса), предписывает добиваться минимума (2.1). Приемник, решающий задачу различения сигналов (различитель), оптимальный по этому критерию, при длительном времени наблюдения будет наиболее "экономичным" из всех, поскольку сумма рисков (штрафов за ошибки) у него окажется наименьшей. Алгоритм функционирования такого приемника заключается в вычислении суммы

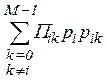                                                                                                                     (2.2)

для всех возможных сигналов () и выборе в качестве решения того сигнала s_i(t), для которого эта сумма окажется минимальной. Поскольку вероятность p_ik равна значению функции правдоподобия (ФП) L_i = P(x(t) | s_i(t)), то сумму (2.2) можно представить в виде

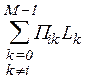.                                                                                                                     (2.2)

Хотя задание рисков П_ik (часто и априорных вероятностей p_i) достаточно произвольно, практическая ценность критерия Байеса достаточно велика, так как он позволяет получить универсальный ответ на вопрос о наилучшей стратегии различения сигналов.

Предположим, что, не имея объективных данных для назначения всех рисков, разработчик стремится лишь к тому, чтобы различитель как можно реже ошибался, т. с. чтобы полная вероятность ошибки

                                                                                                                     (2.3)

была минимальной. Нетрудно видеть, что такой критерий качества, называемый критерием идеального наблюдателя (критерием Котельникова), можно рассматривать как частный случай байесовского, положив в (2.1) П_ii = 0и П_ik = П, , где П -произвольная неотрицательная константа. При этом  = ПР_ош, и минимизация среднего риска равносильна минимизации (2.3).

В частном случае при М = 2 и s₀(t) = 0 рассматриваемая задача переходит в задачу обнаружения детерминированного сигнала s₁(t) на фоне помех с известным статистическим описанием. При этом условные вероятности р₀₁ = P(|) и р₁₀ = = P(|) называются вероятностями ложной тревоги и пропуска (сигнала). Под ложной тревогой понимается факт решения  об обнаружении сигнала при условии, что он в наблюдаемом колебании x(t) не содержится, а под пропуском - решение  о том, что сигнала в x(t) нет при условии, что в действительности он присутствует. Далее для вероятностей ложной тревоги и пропуска будут использованы обозначения р_ЛТ=р₀₁и р_ПС = р₁₀. Средний риск при обнаружении  = р_ЛТ р₀ П₀₁ + р_ПС ´´(1 - р₀)П₁₀, где П₀₁ и П₁₀ - риски, связанные с ложной тревогой и пропуском; р₀ - априорная вероятность отсутствия s₁(t) в x(t). Соотношение (2.3) в этом случае можно представить в виде .

Помимо введенных общих критериев, не связанных с какими-либо допущениями относительно числа М проверяемых гипотез, при обнаружении часто применяют критерий Неймана-Пирсона, предписывающий добиваться минимума вероятности пропуска р_ПС при ограничении сверху на вероятность ложной тревоги р_ЛТ £ р_{ЛТ 0}. При этом предполагается, что правильные решения неравноценны:

При использовании критерия Неймана-Пирсона часто полагают, что априорные вероятности р_i () появления сигналов равны между собой. В этом случае оптимальный различитель должен минимизировать произведение .

2.1.2 Оптимальные методы приема радиосигналов

Разложим помеху относительно сигнала на две составляющие: синфазную с сигналом составляющую с амплитудой U_П1 и ортогональную к сигналу составляющую с амплитудой U_П2. Каждому конкретному виду помех соответствует своя статистическая структура амплитуд U_П1 и U_П2. Векторная диаграмма суммы сигнала и помехи изображена на рис. Здесь U_СП и j_СП - амплитуда и фаза смеси сигнала и помехи.  Такое представление помехи относительно сигнала позволяет разделить все методы приема сигналов на две основные группы:

*   когерентный (синхронный) прием;

*   некогерентный прием (прием по огибающей).

При использовании когерентных методов полностью исключается ортогональная к сигналу составляющая помехи. При этом приемник реагирует только на колебание, равное сумме сигнала и синфазной составляющей помехи.

ОСП при когерентной обработке

, где  -  дисперсия синфазной составляющей помехи.

ОСП при некогерентной обработке

.

Для реализации когерентного приема необходимы опорные сигналы, являющиеся точной копией передаваемых (с точностью до начальной фазы).

При некогерентном приеме, не учитывающем сведения о начальной фазе сигнала, реагирование происходит на суммарное колебание (смесь) сигнала и помехи, имеющее амплитуду U_СП.

Когерентный прием допускают все три вида модуляции (АМ, ЧМ и ФМ), в то время, как детектирование по огибающей возможно выполнить только для АМ и ЧМ.

На практике бывает известна точно только несущая частота сигналов, а начальная фаза известна с некоторой погрешностью. Она определяется ошибкой схемы автоматической подстройки частоты (АПЧ), с помощью которой в приемнике восстанавливается опорный сигнал из принимаемой смеси сигнала с шумом. Системы, в которых опорный сигнал образуется с помощью системы АПЧ, называются квазикогерентными.