Количество информации в сообщении. Энтропия. Пропускная способность канала

1.6.    Количество информации в сообщении. Энтропия.

Пропускная способность канала

Литература:

1. Теория электрической связи /Под ред. Д.Д. Кловского. - М.: Радио и связь, 1999. - С.25-27.

2. Теория передачи сигналов на ж.д. транспорте: Учеб. /Г.В. Горелов и др. - М.: Транспорт, 1999. - С. 128-135.

3. Верещака А.И., Олянюк П.В. Авиационное радиооборудование: Учеб. - М.: Транспорт, 1996. - С. 50-53.

Чтобы сравнивать между собой различные источники сообщений, каналы и другие элементы СПИ, необходимо ввести количественную меру информации, содержащейся в сообщениях и сигналах. Строгие методы такой оценки предложены в 1948 г. К. Шенноном, что послужило началом создания теории информации.

В общем случае сообщению  можно поставить в соответствие вероятность  того, что источник сформирует и пошлет именно это сообщение. Чем менее вероятно сообщение, тем большее количество информации оно несет.

Для количественной оценки информативности сообщений можно использовать любую монотонно убывающую функцию вероятности . Однако, выбирая указанную функцию, к ней предъявляют еще ряд требований:

а) количество информации должно быть аддитивной мерой, т.е. в двух независимых сообщениях количество информации определяется как сумма количеств информации в каждом из них;

б) количество информации в сообщении о достоверном событии равно 0;

в) количество информации не должно зависеть от качественного содержания сообщения (степени важности, возможных последствий его передачи, эмоциональной окраски и т.п.).

Таким образом, естественной мерой количества информации в сообщении может являться величина

.

Основание логарифма в формуле чаще всего выбирается равным 2. В этом случае количество информации выражается в двоичных единицах или битах (от англ. binary digit - «двоичная цифра»). Бит равен количеству информации, содержащемся в сообщении о событии, происходящем с вероятностью  = 0,5 (о событии, которое равновероятно может или происходить или не происходить). Введение двоичных единиц вызвано тем, что в двоичных («цифровых») СПИ используются два символа - 0 и 1. В случае, если эти символы равновероятны  =  = 0,5, то каждый из них несет 1 бит информации.

Ситуации, когда формируемые сообщения (символы) равновероятны, на практике встречаются редко. Обычно вероятности появления различных сообщений неодинаковы. Для оценки количества информации в сообщениях, различающихся вероятностью появления, служит понятие математического ожидания количества информации в 1 сообщении, позволяющее определить среднее количество информации в сообщениях

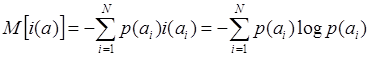.                                                      (1.6.1)

Пример

Пусть р(1) - вероятность передачи логической единицы, р(0) - вероятность передачи логического нуля.

.

Если р(1)=1 или р(0)=1, то сообщение не несет информации, т.к. оно заранее достоверно известно получателю.

Если сообщение состоит из  последовательных независимых двоичных цифр («разрядов»), то количество информации в нем в  раз больше ( бит).

Если источник передает последовательность зависимых между собой сообщений, то получение предшествующих сообщений может изменить вероятность последующего сообщения, а следовательно, и количество информации, содержащейся в нем

.

С понятием количества информации тесно связано и понятие энтропии. Энтропия - основная информационная характеристика источника сообщений. Она характеризует в среднем степень неожиданности сообщений источника, их разнообразие, и поэтому называется также мерой неопределенности сообщений.

, где  и  - значения энтропии до и после передачи сообщения.

Если помех и искажений сигналов в канале связи нет, то = 0.

Основные свойства энтропии:

- энтропия неотрицательна;

- энтропия аддитивна: если рассматривать последовательность  сообщений (символов) как одно укрупненное, то энтропия источника таких укрупненных сообщений будет в  раз больше энтропии исходного источника;

- значение энтропии ;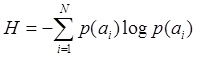

- если ансамбль содержит  различных сообщений, то  ( если все сообщения равновероятны).

В частном случае двоичного источника без памяти (=2, сообщения независимы) энтропия максимальна при р(1)=р(0)=0,5. При этом .

Если сообщения передаются не хаотически, то они передаются не равновероятно и зависимо. При этом энтропия уменьшается.

При =33 (33 буквы)  бит/буква.

Для текстов художественной прозы  бит/буква.

Для поэтических произведений (за счет ритма и рифмы)  бит/буква.

Удельная энтропия - количество информации, в среднем переносимое одним символом.

.

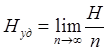Избыточность источника с алфавитом объемом  сообщений

.

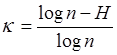Она определяет, какая доля энтропии, максимально возможной для данного алфавита сообщений, не используется источником. Избыточность показывает, насколько можно сократить число символов в последовательности сообщений данного источника, если то же количество информации будет переноситься последовательностью равновероятных и независимых сообщений.

Скорость передачи информации

В дискретных СПИ скорость передачи измеряется числом  символов, передаваемых в единицу времени.  = 1 Бод.

Количество передаваемой информации принято измерять в битах. Максимальное количество информации, которое можно передать одним двоичным символом, равно 1 биту. При использовании не двоичных, а п-чных символов (например, 16-тиричных) максимальное количество информации, которое можно передать одним таким символом, равно . Поэтому источник может обеспечить максимальную скорость выдачи информации (максимальную производительность) 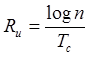 бит/с, где  - длительность 1 символа. При =2 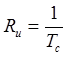 и скорость передачи информации  численно равна технической скорости .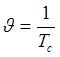

При 2 возможен случай, когда .

Однако нередко . Это наблюдается, когда часть символов (т.н. «служебные») используются для синхронизации или для обнаружения и исправления ошибок.

Количество информации, переданной по каналу связи в условиях помех, меньше количества информации, поступающей на его вход, из-за разрушения части данных помехами.