Циклические коды

3.4.    Циклические коды

Литература:

1. Радиосистемы передачи информации /Под ред. И.Б. Федорова и В.В. Калмыкова. - М.: Горячая линия - Телеком, 2005. - С...

Одним из возможных представлений разрядного кодового слова является его представление в виде полинома степени , такого, что символы  кодового слова являются коэффициентами полинома

.

Здесь  основание используемой системы счисления.

Для упрощения дальнейшего рассмотрения положим  (двоичная система), тогда коэффициенты  могут принимать значения только «0» и «1».

Пример:

.

Представление кодовых слов (комбинаций) в виде полиномов позволяет свести действия над словами к действиям над полиномами.

Так, сложение двоичных полиномов сводится к сложению по модулю 2 коэффициентов при одинаковых степенях , причем результаты выполнения сложения и вычитания двух конкретных полиномов совпадают.

Умножение полиномов производится по правилу умножения степенных функций, а полученные коэффициенты при одинаковых степенях  складываются по модулю 2.

Пример:

.

Деление также осуществляется как деление степенных функций, однако при этом операция вычитания заменяется операцией суммирования по модулю 2.

Линейные коды называют циклическим , если при циклическом сдвиге символов разрешенного кодового слова (комбинации)

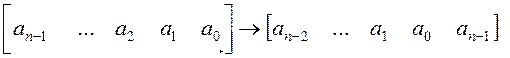
также образуется разрешенное кодовое слово.

Подобная циклическая перестановка проявляется в умножении полинома на

,

.

Умножение полинома на  увеличивает его степень и вызывает удлинение кодового слова (комбинации) на 1 разряд. В связи с ограничением разрядной сети устройств обработки и передачи информации для исключения переполнения член  заменяется на «1».

Тогда .

Важную роль в теории помехоустойчивого кодирования играют неприводимые полиномы, т.е. полиномы которые не могут быть представлены в виде произведения полиномов низших степеней. В теории помехоустойчивого кодирования неприводимые полиномы называются образующими полиномами, поскольку они «образуют» разрешенные кодовые слова (комбинации).

Идея построения циклического кода сводится к тому, что полином степени ,  соответствующий информационного части кодового слова, необходимо преобразовать в полином степени не выше , который без остатка делится на образующий полином кода.

Таким образом, построение разрешенного кодового слова (комбинации) сводится к следующей процедуре:

1. Информационная часть кодового слова длиной  символов представляется в виде соответствующего полинома .

2. Полином  умножается на , т.е. производится сдвиг разрядного слова на  разрядов ( число проверочных разрядов).

3. Полином  делится на образующий полином  кода, степень которого равна . При делении образуется частное  такой же степени, что и , и остаток

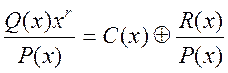, т.е. ,

.

Соответственно, разрешенное кодовое слово можно получить двумя способами:

1) умножением полинома степени  на образующий полином  кода;

2) умножением полинома степени  на  (т.е. сдвигом информационной части кодового слова на  разрядов влево) и добавлением остатка, полученного в результате деления произведения  на образующий полином  кода.

В  первом случае информационные и проверочные символы не отделены друг от друга (т.е. код получается неразделимым). Это затрудняет декодирование. Во втором случае формируется разделимый код: информационные разряды занимают старшие позиции, остальные разряды – проверочные.

Пример:

Построить циклический код с кодовым расстоянием  3, т.е способный обнаруживать и исправлять однократные ошибки..

а. Исходя из требуемого  3 определим количество  проверочных разрядов, равное показателю степени образующего полинома

    (или ).

Т.к. , то  4 и . Минимальное значение = 3.

Следовательно, необходим код (7,4). Для = 3 по таблице неприводимых полиномов находим образующий полином кода .

б. Полином .

.

в. 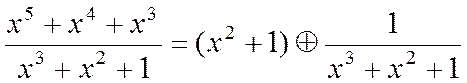,   т.е. 1.

г. По 2-му способу

.

Данный полином соответствует кодовой комбинации	0111	001

д. По 1-му способу

Таким образом, кодовое слово (комбинация) имеет вид

0100011.

Схема кодера, реализующего 2-й способ циклического кодирования, строится по образующему полиному  и представляет собой схему деления на . Один из вариантов кодера представлен на рисунке 3.3.1. Схема состоит из  элементов регистра сдвига (триггеров) и сумматоров по модулю 2, число которых равно числу знаков сложения в . Исходное состояние триггеров – нулевое.

Декодирование циклического кода основано на том, что любой кодовый полином  должен делиться на образующий полином  без остатка. Если принятое кодовое слово не принадлежит коду, то соответствующей ему полином не делится нацело на .

Определение синдрома делением на  требует меньше оборудования, чем его вычисление в соответствии с формулой (). Таким образом, основным элементом в схеме декодера является схема деления, называемая генератором синдромов (ГС) (рисунок 3.3.2).