Круговая диаграмма

Круговая диаграмма

При экспериментальных количественных исследованиях волноводных систем, их узлов и элементов приходится измерять координаты экстремальных значений электрического поля, Кс,

коэффициенты отражения, сопротивления и др. величины. Для графического отображения результатов измерений, для пересчета параметров линии передачи из одного сечения в другое, осуществление согласования нагрузки с волноводом, для выяснения физики работы отдельных узлов и элементов волноводного тракта, решения многих других задач широко применяется круговая диаграмма Вольперта-Смита. Созданная более 40 лет тому назад, круговая диаграмма не потеряла своего значения и в настоящее время. Наглядность, физичность, быстрота решения многих задач и получения полезной информации об СВЧ устройствах – таковы основные достоинства круговой диаграммы.

Круговая диаграмма строится на плоскости комплексного переменного и размещается внутри единичного круга. При построении за основу берется формула типа  

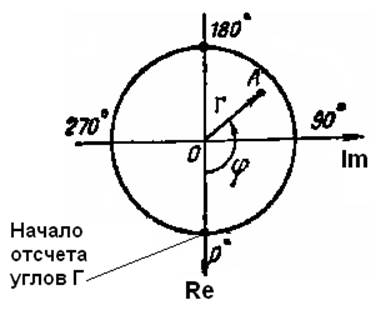
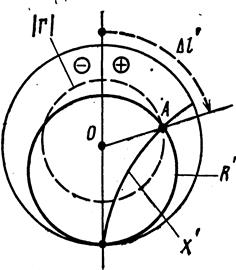
На рис. 1 комплексный коэффициент отражения изображен вектором ОА,

,  

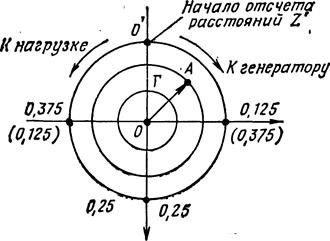
На практике удобнее пользоваться не углом   φ=2βl , а пропорциональной ему величиной  l′=l′/λB,  и тогда φ=2βl=4πl/λB=4πl′. Отсюда следует, что пространственный период круговой диаграммы составляет  ∆l′=0.5 или  ∆l=0.5λB. Нормированное значение  l′ иногда называют приведенным ( волновым, реже – электрическим) расстоянием.  Его отсчет производится либо в направлении к генератору ( по ходу часовой стрелки, либо в направлении к нагрузке (против хода часовой стрелки).

За начало отсчета l′=0 принимается сечение  Emin, так как оно точно и просто находиться при измерениях. В этом сечении фаза коэффициента отражения φ=π (падающая и отраженная волны противофазны).

Соответственно сечение, где l′=0.25, есть сечение максимума напряженности электрического поля Emax.

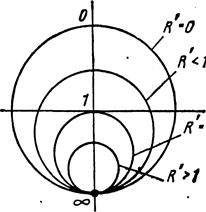
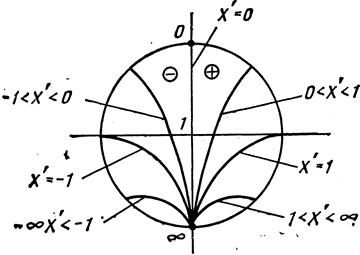
Семейство линий                           представлено на рис.2 концентрическими окружностями. Так как                                                          , то эти же окружности есть линии постоянных значений       и      . В центре диаграммы,                            что соответствует режиму бегущих волн. На периферии диаграммы

, что соответствует режиму стоячих волн. Остальные точки диаграммы, для которых                                       ,  соответствуют режиму смешанных волн.

На диаграмму наносят также линии постоянных активных R′ и реактивных X′ сопротивлений (рис.3, рис.4) в соответствии с формулой

(*)

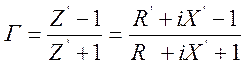
Множество точек правой половины диаграммы изображает индуктивные сопротивления, так как Х′ > 0, а левой половины – емкостные сопротивления, так как Х′ < 0.

Таким образом, некоторая точка (например, точка А) на диаграмме Вольперта-Смита изображает (рис.5): конец вектора, представляющего коэффициент отражения Г с ортогональными координатами                                                  и  ∆l′; сопротивление Z′=R′+iX′ с ортогональными координатами R′ и X′.

			Рис.5 Различные координаты точки на круговой диаграмме

Оба представления эквивалентны и широко применяются на практике.

Диаграмма с нанесенными линиями R′ и X′ получила название диаграммы полных сопротивлений.

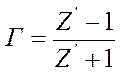
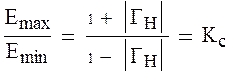Покажем, что в сечении Emin  коэффициент отражения Г=-|Г|. Отсюда из и                                                следует, что Z′=Kc.

Аналогично можно показать, что в сечении Emin коэффициент отражения Г=|Г| и сопротивление                                      

В силу того, что в сечениях Emax и Emin сопротивления активные, эти сечения носят название резонансных, о чем уже упоминалось выше.

Наряду ( и наравне) с диаграммой сопротивлений применяется диаграмма проводимостей. Обозначая полную проводимость через                

Получаем, что

Откуда

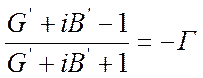
Сравнивая последнюю формулу с (*), заключаем, что: комплексные числа Z′ и

на круговой диаграмме изображаются диаметрально противоположными точками (рис.6);

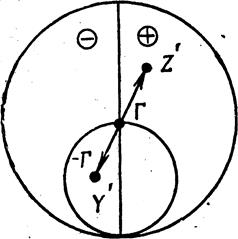
семейство линий активной проводимости G′ совпадает с семейством линий активного сопротивления R′, а семейство линий реактивной проводимости В′ - с семейством линий реактивного сопротивления Х′, что позволяет использовать одни и те же бланки диаграмм как при работе с сопротивлениями, так и при работе с проводимостями;