Круговая диаграмма, страница 2

	Сечение Emin		Сечение Emax

 

                                                                                                                                             

	Рис.7 Сравнение круговой диаграммы сопротивлений и круговой диаграммы проводимостей

 

так как точки правой половины диаграммы соответствуют положительной реактивности, на диаграмме проводимостей они изображают емкостные проводимости. Соответственно точки левой половины диаграммы проводимостей изображают индуктивные проводимости (рис.7);

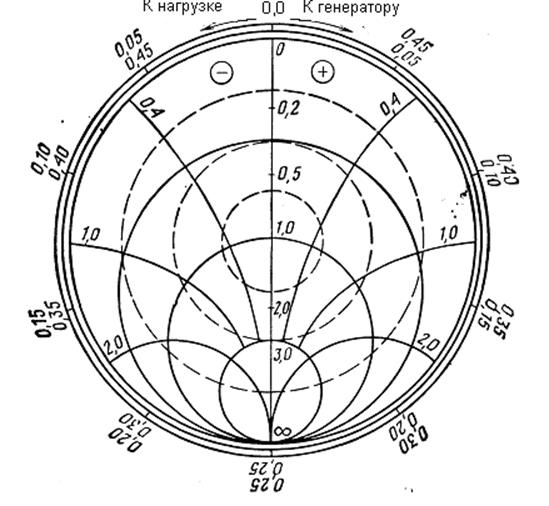
там, где на диаграмме сопротивлений находится сечение Emin, на диаграмме сопротивлений (проводимостей) цифры, обозначающие величину R′ (G′) линий

R′=const (G′=const), приведены на линиях Emin и Emax. Одновременно эти цифры обозначают величину Кб и Кс на линиях |Г|=const.

	Рис.8 Круговая диаграмма

 

Цифры, обозначающие Х′ (В′) на линиях Х′=const (В′=const), приведены на внешней окружности диаграммы.

Общий вид круговой диаграммы изображен на рис.8.

Рассмотрим некоторые задачи, решаемые с помощью круговой диаграммы.

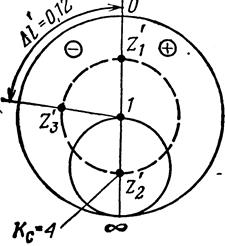
Задача 1.  С помощью измерительной линии найдено, что в линии передачи

Кс=4.Требуется нанести на круговую диаграмму точки, изображающие сопротивления линии передачи:

1)  в сечении Еmin – точка Z′1;

2)  в сечении Еmax – точка Z′2;

3)  в сечении, удаленном от сечения Еmin   к нагрузке на расстояние ∆l=0.12λв, - точка Z′3.

Решение представлено на рис.9.

Следует обратить внимание на то, что линия Кс=const ( например, в этой задаче Кс=4) есть геометрическое место точек, изображающих сопротивление в разных сечениях одной и той же линии передачи.

Рис.9 Сопротивление в разных сечениях одной и той же линии предачи

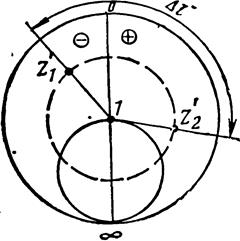
Задача 2.  Дано численное значение сопротивления Z′1 в каком-то одном сечении линии передачи. Требуется найти значение сопротивления Z′2  в другом сечении, отстоящем от первого сечения на расстоянии ∆l′.

Решение представлено на рис.10.

                    

	Рис.10 Пересчет сопротивления из одного сечения линии передачи в другое

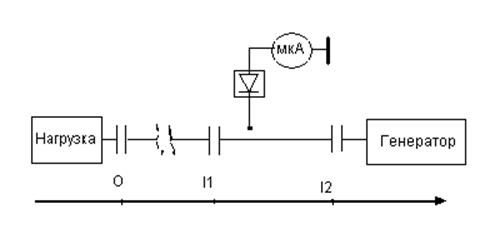
Задача 3. Измерение сопротивления нагрузки Z′н с помощью измерительной линии.

Структурная схема установки представлена на рис.11, где координаты l1 и l2 обозначают диапазон перемещения зонда измерительной линии.

Требуется по результатам измерений, проведенных с помощью измерительной линии, нанести на круговую диаграмму точку, изображающую сопротивление нагрузки, и найти численное значение Z′н.

Эту задачу удобно разделить на две части:

измерение сопротивления в сечении Еmin;

пересчет сопротивления из сечении Еmin  в эквивалентное сечение нагрузки.

Для измерения сопротивления в сечении Еmin  находим численные значения напряженности электрического поля Еmax  и Еmin, а по ним значение Кб=Emin/Emax. В сечении Еmin сопротивление Z′=Кб, что позволяет нанести эту точку на круговую диаграмму (рис. 12).

Рис.12 Определение сопротивления нагрузки при помощи круговой диаграммы

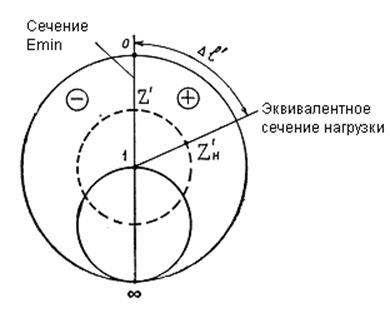
Для пересчета найденного сопротивления Z′ из сечения Еmin  в эквивалентное сечение нагрузки необходимо знать расстояние (обозначим его через ∆l) между этими сечениями и длину волны в волноводе λв. Для измерения ∆l сначала находим координату lmin сечения Еmin  при подсоединенной искомой нагрузке, а затем координату lэкв эквивалентного сечения нагрузки. Как правило, сечение нагрузки (l=0 на рис.11)  бывает недоступно для зонда измерительной линии, и поэтому используется понятие эквивалентного сечения нагрузки: вместо координаты нагрузки измеряется координата lэкв на участке l1<l<l2. При измерении lэкв удобно использовать режим короткого замыкания – нагрузка отсоединяется удаленными от нагрузки на целое число полуволн и поэтому являются эквивалентными сечениями нагрузки. В результате находим ∆l′=|lmin-lmax|/λв  и точку Z′н  на круговой диаграмме (рис.12).

Рекомендуется такой порядок действий:

при подключенной нагрузке находим Кб=Emin/Emax и lmin – координату сечения Emin;

после отключения нагрузки и создания короткого замыкания находим lэкв – координату эквивалентного сечения нагрузки и λв.

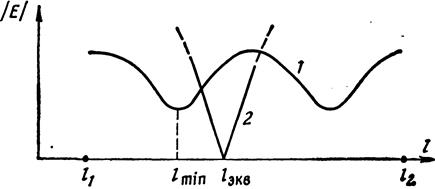
Далее находим ∆l′ и наносим точку Z′н  на диаграмму. Здесь следует быть внимательным при определении направления отсчета ∆l′ - к нагрузке или к генератору: направление определяется от сечения lmin к сечению lэкв (рис.13)

Рис.13 К измерению сопротивления нагрузки при помощи измерительной линии

	1-  распределение поля при подключенной нагрузке 2-  распределение поля в режиме короткого замыкания