



Лекция10. Устойчивость линейных стационарных систем
Теория устойчивости динамических систем развивалась в рамках математики и механики еще до возникновения самостоятельной науки об управлении. Важные результаты в этой области принадлежат русскому математику А.И. Ляпунову. Формулировка понятия устойчивости по Ляпунову основана на понятиях возмущенного и невозмущенного движения системы, которые рассматриваются в двух вариантах: для переменных состояния системы и в отклонениях.
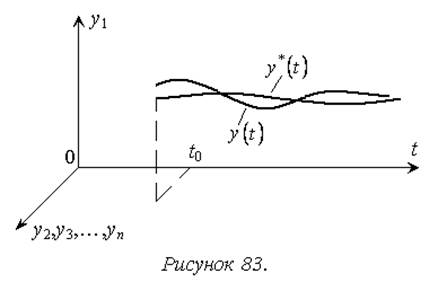
В первом случае (рисунок 83) рассматриваются законы
изменения переменных состояния системы в установившемся процессе, в частном
случае их значения в состоянии равновесия, ![]() , i=1,2,…,n,
- по Ляпунову это невозмущенное движение. Возмущенное движение yi(t), i=1,2,…,n, – это законы изменения переменных состояния системы в переходном
процессе, то есть свободное движение системы после начального отклонения,
вызванного любыми причинами.
, i=1,2,…,n,
- по Ляпунову это невозмущенное движение. Возмущенное движение yi(t), i=1,2,…,n, – это законы изменения переменных состояния системы в переходном
процессе, то есть свободное движение системы после начального отклонения,
вызванного любыми причинами.
Во втором случае возмущенное движение вводится как
отклонение ![]() . При такой трактовке невозмущенное
движение имеет вид
. При такой трактовке невозмущенное
движение имеет вид ![]() . Такая трактовка более удобна
для анализа процессов в системе.
. Такая трактовка более удобна
для анализа процессов в системе.
Невозмущенное движение системы (установившийся
процесс) ![]() называется устойчивым, если при заданном
сколь угодно малом e>0 существует такое d=d(e)>0, что при
начальных условиях
называется устойчивым, если при заданном
сколь угодно малом e>0 существует такое d=d(e)>0, что при
начальных условиях ![]() , i=1,2,…,n
существует такое t1>t0, что при t1<t<∞ выполняется условие
, i=1,2,…,n
существует такое t1>t0, что при t1<t<∞ выполняется условие ![]() , i=1,2,…,n,
то есть возмущенное движение ограничено.
, i=1,2,…,n,
то есть возмущенное движение ограничено.
Если условия определения устойчивости по Ляпунову
выполняются,
и ![]() , то соответствующее невозмущенное движение
, то соответствующее невозмущенное движение
![]() называется асимптотически устойчивым.
называется асимптотически устойчивым.
Для линейных стационарных систем под устойчивостью
понимают именно асимптотическую устойчивость, возмущенное движение по Ляпунову представляет
собой переходную составляющую процесса в системе yп(t). Таким образом, линейная стационарная система
устойчива, если ![]() .
.
Если получено общее дифференциальное уравнение линейной стационарной системы
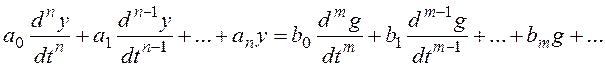 .
.
то переходная составляющая процесса в системе определяется как решение соответствующего однородного уравнения
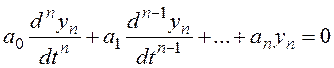 .
.
и имеет вид, например,
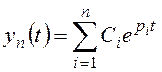 , (10.1)
, (10.1)
где pi– корни характеристического уравнения
![]() или D(s)=0, где D
– характеристический полином системы,
являющийся знаменателем ее передаточных функций.
или D(s)=0, где D
– характеристический полином системы,
являющийся знаменателем ее передаточных функций.
Выражение (10.1) соответствует случаю отсутствия кратных корней характеристического уравнения. Его примем за основу в дальнейших рассуждениях. Основные выводы остаются справедливыми и при наличии кратных корней.
Прежде всего, отметим, что поскольку коэффициенты Ci в (10.1)
определяются в зависимости от начальных условий и в общем случае произвольны,
то для выполнения условия ![]() необходимо, чтобы все
слагаемые в (10.1) независимо друг от друга стремились к нулю. Рассмотрим их
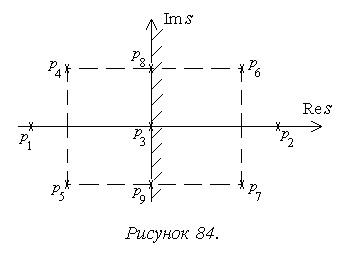
поведение при различных видах корней, отображая последние на плоскости
корневого годографа (рисунок 84):
необходимо, чтобы все
слагаемые в (10.1) независимо друг от друга стремились к нулю. Рассмотрим их
поведение при различных видах корней, отображая последние на плоскости
корневого годографа (рисунок 84):
1. Вещественный отрицательный корень p1=-a (a>0). Слагаемое в выражении (10.1) для переходной
составляющей имеет вид ![]() и с течением времени монотонно
стремится к нулю (рисунок 85а).
и с течением времени монотонно
стремится к нулю (рисунок 85а).
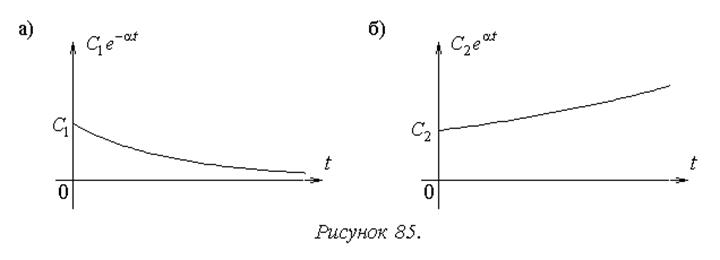
2. Вещественный положительный корень p2=a>0. Слагаемое в
выражении (10.1) для переходной составляющей имеет вид ![]() и
с течением времени монотонно стремится к бесконечности (рисунок 85б).
и
с течением времени монотонно стремится к бесконечности (рисунок 85б).
3. Нулевой корень p3=0. Слагаемое в выражении (10.1) для переходной составляющей остается константой.
4. Комплексно сопряженные корни с отрицательной
вещественной частью p4,5=–a±jb (a>0). Слагаемое в выражении (10.1) для переходной
составляющей имеет вид ![]() и определяет
затухающие колебания (рисунок 86а).
и определяет
затухающие колебания (рисунок 86а).
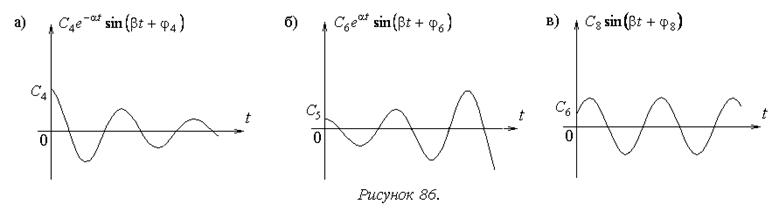
5. Комплексно сопряженные корни с отрицательной
вещественной частью p6,7=a±jb (a>0). Слагаемое в выражении (10.1) для переходной
составляющей имеет вид ![]() и определяет
расходящиеся колебания (рисунок 86б).
и определяет
расходящиеся колебания (рисунок 86б).
6. Мнимые корни p8,9=±jb. Слагаемое в выражении (10.1) для переходной
составляющей имеет вид ![]() и определяет колебания
с постоянной амплитудой (рисунок 86в).
и определяет колебания
с постоянной амплитудой (рисунок 86в).
Таким образом, для устойчивости системы ![]() необходимо и достаточно, чтобы корни
характеристического уравнения (характеристического полинома) лежали в левой
полуплоскости комплексной плоскости:
необходимо и достаточно, чтобы корни
характеристического уравнения (характеристического полинома) лежали в левой
полуплоскости комплексной плоскости: ![]() .
(10.2)
.
(10.2)
Если имеется хотя бы один корень в правой полуплоскости, система неустойчива.
Если имеется нулевой корень, а остальные удовлетворяют условию (10.2), система находится на апериодической границе устойчивости. Отметим, что это имеет место, если свободный член характеристического полинома an=0.
Если имеется пара мнимых корней, а остальные удовлетворяют условию (10.2), система находится на колебательной границе устойчивости.
Таким образом, на плоскости корневого годографа областью устойчивости является левая полуплоскость, границей устойчивости – вертикальная ось.
Для того, чтобы формально получить замкнутую область
устойчивости, вводят третий вид границы устойчивости, соответствующий корням с ![]() . Отметим, что это имеет место, если в
характеристическом полиноме
. Отметим, что это имеет место, если в
характеристическом полиноме ![]() .
.
Условие (10.2) неудобно для практического использования, так как задача определения корней характеристического полинома для системы высокого порядка может оказаться весьма трудоемкой. Его основная роль состоит в том, что оно является основой для получения системы условий и критериев устойчивости, применяемых на практике.
Необходимое условие устойчивости
Пусть характеристический полином системы имеет только отрицательные вещественные корни и пары комплексно сопряженных корней с отрицательной вещественной частью, то есть система устойчива. Представим его в виде произведения
![]()
![]()
![]()
Сопоставляя полученное выражение с общей формой записи
характеристического полинома ![]() , нетрудно убедиться,
что при a0>0 и в
случае устойчивости системы в нем будут присутствовать все степени s,
причем обязательно с положительными коэффициентами.
, нетрудно убедиться,
что при a0>0 и в
случае устойчивости системы в нем будут присутствовать все степени s,
причем обязательно с положительными коэффициентами.
Отсюда следует необходимое условие устойчивости: все коэффициенты характеристического полинома должны быть одного знака.
Это условие удобно для использования и является достаточным для систем первого и второго порядка.
Убедимся в этом.
Для системы первого порядка:
![]() ,
,
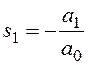 .
.
При a0>0 и a1>0 получаем вещественный отрицательный корень, то есть система устойчива.
Для системы второго порядка:
![]() ,
,
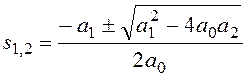 .
.
При положительных a0, a1 и a2 возможны два случая:
- при ![]() два отрицательных
вещественных корня;
два отрицательных
вещественных корня;
- при ![]() пара комплексно
сопряженных корней с отрицательной вещественной частью.
пара комплексно
сопряженных корней с отрицательной вещественной частью.
В обоих случаях система устойчива.
Для систем третьего и более высокого порядка при выполнении необходимого условия для окончательного ответа на вопрос об устойчивости системы требуется дополнительно применить одно из достаточных условий (критериев устойчивости).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.