Методы измерения дальности. Импульсный метод определения дальности. Частотный метод измерения дальности. Фазовые методы измерения дальности, страница 2

     Электронная шкала создается  с помощью стабильного масштабного генератора. Воспроизведение меток дальности на экране ЭЛТ можно осуществить различными методами. Наиболее удобно для этой цели применять двухлучевую трубку. В этом случае один луч используется для развертки радиолокационных сигналов, а другой — для создания электронной шкалы. Подобную же картину можно получить в однолучевой трубке, если к отклоняющим пластинам подводить поочередно радиолокационные сигналы и метки дальности. Применение электронной шкалы дает ряд преимуществ по сравнению c механической шкалой, в частности, исключается влияние нестабильностей источников питания на точность отсчета, отсутствуют ошибки параллакса, облегчаются условия наблюдения за отраженными сигналами. Недостатком применения электронной шкалы является наличие ошибок интерполяции и усложнение схемы.

ЧАСТОТНЫЙ МЕТОД ИЗМЕРЕНИЯ ДАЛЬНОСТИ

Принцип измерения дальности с помощью частотной модуляции.

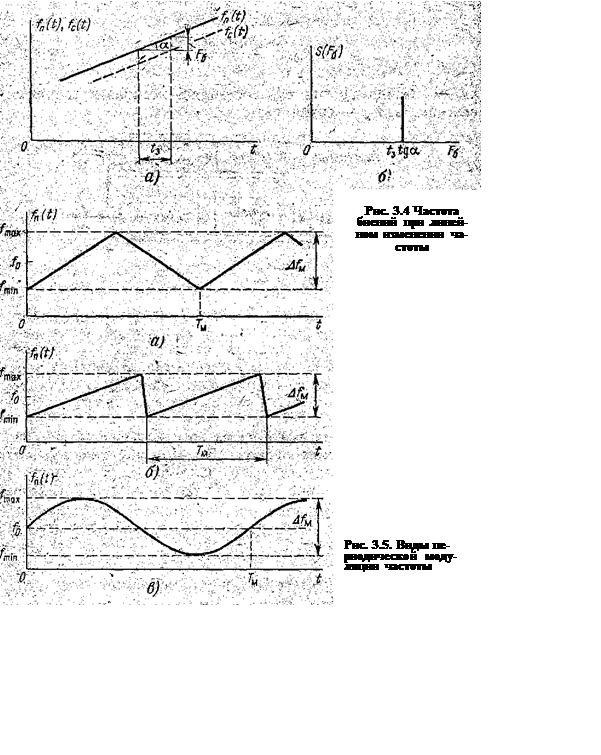
Определение дальности до цели при использовании частотной модуляции (ЧМ) основано на измерении приращения частоты передатчика за время  распространения сигнала до цели и обратно. Если предположить, что частота передатчика f_п (t) может изменяться по линейному закону, то изменение частоты отраженного сигнала f_с (t) а будет запаздывать на время t_з= 2D/c (рис. 3.4, а). В результате смешения этих колебаний образуются биения, огибающая которых является, чисто гармоническим колебанием, т. е. ее спектр состоит из одной спектральной линии (рис. 3.4, б). Величина приращения частоты (частота биений) легко определяется из рис. 3.4,а  и равна

F_б= t_з tgα = t_з·df_п(t)/dt = 2D/c·df_п(t)/dt              (2)   т.е.  пропорциональна дальности.

На практике используются различные виды периодической модуляции частоты, например: симметричный и несимметричный пилообразные законы (рис. 3.5, а, б), синусоидальный закон (рис. 3.5, в). На всех упомянутых рисунках масштаб не выдержан, так как всегда средняя частота  f₀ » Δf_м,  где Δf_м - девиация частоты (полоса качания).

1.  Структурная схема простейшей РЛС с ЧМ.

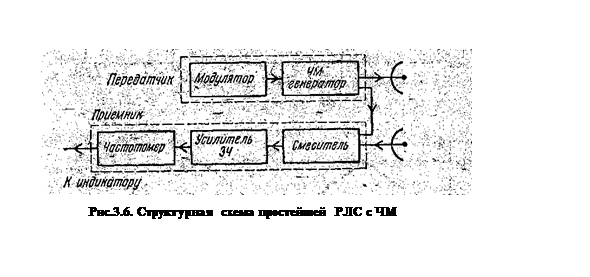
Рассмотрим случай симметричного пилообразного закона ЧМ. Структурная схема такой РЛС (дальномера) приведена на рис. 3.6.

Сигнал передатчика попадает на вход приемника (в смеситель) через антенну, либо по специальной линии передачи. Отраженный сигнал от неподвижной цели, также  попадающий  на вход приемника,  запаздывает  на время t_з (рис. 3.7). В результате смешения (сложения) двух колебаний на входе приемника образуются биения.

Мгновенная частота биений равна абсолютному значению разности мгновенных значений частот излучаемого отраженного сигналов

|F_б (t)| = | f_п(t) - f_с(t) |,

хотя формально можно учитывать знак частоты F_б (t). Сказанное иллюстрируется рис. 3.7 б,в. Частоту биений, которая в течение большей части периода модуляции Т_м остается постоянной,  назовем основной. Ее значение, как видно из рис. 3.7а и формулы

(2), равно

F_б0 = γt_з                                           (3)

Так как  скорость   изменения частоты γ = df_п/dt=2∆f_мF_м, (где Δf_Μ — девиация частоты, а F_м – частота модуляции), то основная частота биений  

F_бо= 4∆f_мF_мD/c                   (4)    

Причем обычно частота ∆f_м составляет несколько десятков МГц, а

F_м – сотни Гц.

Функция |F_б (t)|  (рис.3.7в) отличается от F_бо.  Небольшие отрезки времени, равные времени запаздывания  t_з, в течение которых частота не остается постоянной

(рис. 3.7в), называют зонами обращения. В средних точках этих зон функция F₆ (t) проходит через нуль. Влияние зон обращения тем меньше, чем лучше выполняется неравенство Т_м >> t₃.