Оптимальная обработка при обнаружении радиолокационных сигналов. Обнаружение радиолокационных сигналов как статистическая задача, страница 3

Значения условных вероятностей правильного обнаружения Dи ложной тревоги F задаются для разрешаемого объема пространства. Если в РЛС кругового обзора имеется n разрешаемых объемов за период обзора, то в среднем за это время будет т=Fп «ложных отметок». Такие отметки воспринимаются оператором; следящим за индикатором кругового обзора, как отметки цели, хотя отдельных шумовых выбросов на экране при этом может быть гораздо больше. Поэтому, задаваясь допустимым наличием т ложных отметок за период обзора, имеем F = т/п, например, при т = 1 иn = 10⁶ требуемая вероятность ложной тревоги F == 10^-6.

В задачах радиолокации, когда наличие цели (условие Н₁) встречается сравнительно редко и трудно даже судить о стоимости пропуска цели, более важную роль играют те случаи, когда Н₁ выбрано неправильно, т. е возникает ложная тревога. Она особенно опасна, так как может, например, привести к значительному увеличению числа операций в ЭВМ, используемой в автоматизированной системе УВД, а также другим действиям, имеющим высокую стоимость. Поэтому в радиолокации задаются заметно меньшей вероятностью ложной тревоги по сравнению с вероятностью пропуска цели F<<  1 — D и требуют согласно (18) максимизации вероятности правильного обнаружения D, которая должна быть достаточно близкой к единице (например, по одной из рекомендаций ICAO для РЛС УВД D= 0,9, F = 10^-7).

Это требование соответствует критерию Неймана-Пирсона, в соответствии с которым оптимальный приемник должен обеспечивать получение наибольшей вероятности правильного обнаружения при заданных значениях ложной тревоги и отношении сигнал/шум; при использовании любого приемника для тех же значений F и отношении сигнал/шум вероятность правильного обнаружения будет меньше.

Отношение правдоподобия.

Рассмотрим условия выполнения весового критерия (18), для чего найдем вероятности правильного обнаружения и ложной тревоги Dи F. Воспользуемся теоремой Котельникова. При этом следует сделать предположение об ограниченности спектра принимаемого сигнала х(t) и помехи п(t) в полосе частот 0≤ f ≤f_макс. Тогда функция х(t) однозначно отображается своими дискретными значениями х₁,х₂,..., х_т, отсчитанными через временные интервалы Δt= l/2f_макс.  Вся совокупность отсчетов называется выборкой. Если функцию х(t) ограничить интервалом времени T₀, то для ее отображения требуется m=T/Δt=2f_максТ₀  отсчетов.

Каждая реализация случайной функции х(t) при наличии как. помех, так и полезного сигнала "определяется многомерной плотностью распределения вероятностей

w_сп(х₁,х₂,…,х_т),а если полезного сигнала нет, то плотностью распределения помехи w_п(х₁,х₂,…,х_т). Совместная вероятность нахождения значений х в интервале

х₁, x₁+dx₁;   х₂, x₂+dx₂  и т. д. равна  w_сп(х₁,х₂,…,х_т)dx₁dx₂...  dx_m (аналогичная зависимость справедлива для плотности распределения помехи w_n). Так как значения х_1,х₂,...  определяют функцию х(t) однозначно, то указанная вероятность определяет вероятность реализации функции х(t).

Для принятия решения о наличии или отсутствии цели следует разбить все множество выборок на области X₁ наличия сигнала (решение A₁) и Х₀ (решение A₀) отсутствия сигнала. Условную вероятность правильного обнаружения найдем как вероятность попадания выборки  х_1,х₂,...  в область X₁ при условии наличия сигнала (плотность распределения w_сп), а условную вероятность ложной тревоги — как вероятность попадания этой выборки в область X₁ при условии отсутствия сигнала (плотность распределения w_п). Таким образом,

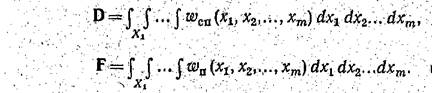                                 (19)   

Интегрирование производится в области X₁ по всем переменным. Граница этой области выбирается на основании весового критерия обнаружения (18), так что

                                                                              (20)

где

                                                             (21)

называется отношением правдоподобия (так как более правдоподобно то из решений А₁ и А₀, которому соответствует большая плотность вероятности получения данной реализации х(t)).

Для значений х_1,х₂,.., х_m, для которых отношение правдоподобия l(х_1,х₂,.., х_m) > l₀   , все подынтегральное выражение положительно. Значения же х_1,х₂,.., х_m, для, которых l<1₀, уменьшают весь интеграл. Поэтому максимизация разности (D — l₀F) требует так выбирать границы  области X₁ чтобы выполнялось неравенство l > l₀. Отсюда вытекает правило принятия решения:

решение А₁ (сигнал есть), если   l(х_1,х₂,.., х_m) > l₀ ;                                      (22)                   

решение А₀ (сигнала нет), если   l(х_1,х₂,.., х_m) < l₀   

Весовой множитель l₀ (17), не зависящий от принимаемого сигнала, можно рассматривать как некоторый порог. Для принятия решения о наличии или отсутствии сигнала надо вычислить отношение правдоподобия  l[х(t)]  принятого сигнала х(t) и сравнить его с порогом l₀.