Оптимальная обработка при обнаружении радиолокационных сигналов. Обнаружение радиолокационных сигналов как статистическая задача, страница 2

Можно принять

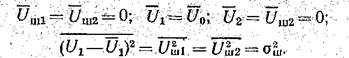
Критерии оптимального обнаружения.

При обнаружении возможны два неизвестных и взаимоисключающих условия, которые иногда именуются альтернативными гипотезами: условие Н₁ — сигнал (цель) есть; условие Н₀  — сигнала (цели) нет.

Приемник на основе анализа функции х(t) должен вынести решение о наличии или отсутствии сигнала (цели). Решения обозначим: А₁ — сигнал (цель) есть; А₀ — сигнала (цели) нет.

Одно из решений правильное, а другое — ошибочное, так что возможны четыре варианта совмещения решения и условия:

- А₁H₁  — правильное обнаружение; 

- А₀H₁  — пропуск цели;

- А₁H₀  —  ложная тревога;

-  А₀H₀ — правильное необнаружение.

Обычно определение априорных вероятностей наличия и отсутствия целей р(А₁) и р(А₂), а также вероятностей совмещения (безусловных вероятностей) р(А₁H₁), р(А₀H₁),

р(А₁H₀), р(А₀H₀) связано с практическими трудностями, и поэтому при проектировании, испытании и эксплуатации РЛС используются условные вероятности. Вероятность со- бытия А₁, вычисленная при условии, что имело место H₁, именуется вероятностью правильного обнаружения

D = р(А₁/H₁).                                        (6)

Аналогично,  вероятность пропуска  

D₀ = р(А₀/H₁).                                        (7)

Правильное обнаружение и пропуск образуют полную группу несовместных событий, так что     

D + D₀ = 1.                                             (8)

Далее имеем вероятность ложной тревоги (ложного обнаружения)

F = р(А₁/H₀)                                          (9)               и вероятность правильного необнаружения

F₀ = p(A₀\H₀),                                     (10)

причем, как и в (8),

F + F₀=1.                                                 (11)

Из сказанного следует, что при обнаружении возможны два вида ошибок: пропуск цели и ложная тревога. Степень нежелательности этих ошибок различна, что надо учиты-  вать при принятии решения. Делается это посредством некоторой величины  —  cтоимости ошибок. Систему обнаружения характеризуют средней стоимостью или средним риском, которая вычисляется по правилу нахождения математического ожидания:

                             (12)

где г₀₁ — стоимость пропуска, а г₁₀ — стоимость ложной тревоги.

Воспользуемся правилами умножения   вероятностей:

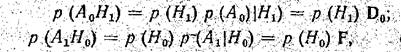                                             (13)

где р(H₁) и р(H₀) —  априорные вероятности соответственно наличия и отсутствия сигнала.      Подставляя (13) в (12), получаем средний риск в виде       

                           (14).

Оптимальной обработкой сигнала (оптимальным приемником) будем считать такую, которая характеризуется минимумом среднего риска. Данная оценка обработки  математической статистике и именуется байесовской оценкой. Она естественна для наблюдателя, который должен принять большое число решений в одинаковых условиях.

Для использования минимума среднего риска в качестве критерия обнаружения («критерий Байеса») должны быть установлены стоимости ошибок г₁₀ и г₀₁ и известны априорные вероятности р(H₁) и р(H₀). Если, например, принять, стоимости ошибок

r₀₁ = r₁₀ = 1,

т. е. полагать, что пропуск сигнала и ложная тревога одинаково опасны, то средний риск равен

,                           (15)

т. е. суммарной вероятности ошибки.

Условие минимума этой суммарной вероятности ошибки называется критерием идеального наблюдателя. Он соответствует критерию идеального приемника, и широко используется в задачах радиосвязи, где ложное обнаружение и пропуск одинаково нежелательны.

Представим теперь в формуле (14) вероятность пропуска цели как  D₀= 1 — D, тогда    

              (16)           где весовой множитель

                                                  (17)

включает только стоимости ошибок и априорные вероятности, т, е. не зависит от принимаемого сигнала.             

_—

Следствием минимума среднего риска  r   является максимум разности

D—l₀F = max,                                                               (18)

что именуется весовым, критерием.

Если задаться  l₀  и сравнивать оптимальную и неоптимальные системы, то

D_опт—l₀F_опт ≥ D—l₀F, или

D_опт≥ D + l₀(F_опт –F).

Таким образом.  при  F<F_опт  должно быть D < D_oпт , т.е. оптимальная система дает наибольшую вероятность правильного обнаружения среди всех систем, имеющих вероятность ложной тревоги не больше, чем у оптимальной.