Исследование помехоустойчивости оптимальных приёмников бинарных сигналов, страница 3

Необходимый объем выборки может быть уменьшен еще примерно в 2 раза, если для формирования оценки  воспользоваться методом усреднения многократных отсчетов, смысл которого заключается в том, что найденная усредненная оценка центра рассеяния параметра имеет меньшую случайную погрешность, чем отдельные отсчеты, по которым она находится. Это означает, что несколько () коротких выборок объемом по  могут обеспечить точность, достижимую выборкой объемом . Как известно, при оценке погрешности определения центра распределения при малых объемах выборок () применяется распределение Стьюдента, при котором доверительное значение погрешности оценки центра распределения находится как

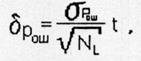
где     квантиль распределения Стьюдента от ;

Таким образом, задаваясь ожидаемой вероятностью ошибки и требуемой точностью ее экспериментального определения, определяем  и  с учетом обеспечения выполнения соотношения . Рекомендуется выбирать  в интервале 2 … 8.

Таблица 1 - Квантили распределения Стьюдента

ПОДГОТОВКА К РАБОТЕ

1. Изучить схемы оптимальных приёмников АМ, ЧМ и ФМ сигналов и начертить их в отчёте по работе.

2. Познакомиться с временными диаграммами и спектрами сигналов во всех сечениях трактов приёмников.

3. Уяснить расчёт вероятности ошибки приёма символов в зависимости от ОСПШ для всех видов модуляции. Проанализировать графики этих зависимостей с целью определения значений ОСПШ и соответствующих им значений вероятности ошибки р, которые ожидаются в экспериментах.

4. Рассчитать объём выборки символов N, необходимый для экспериментальной оценки вероятности ошибки р с приемлемой точностью.

5. Уяснить содержание исследований и особенности работы модели оптимальных приёмников.

СОДЕРЖАНИЕ ИССЛЕДОВАНИЙ

1. Наблюдение временных диаграмм в сечениях схем приемников при больших и малых отношениях сигнал/шум

1.1 Запустить на выполнение программу modulat.exe.

При этом на экран выводится графическое окно с меню выбора вида модуляции. Выбор осуществляется курсором с последующим нажатием клавиши «Enter».

При выборе какого-либо вида модуляции генерируется код 1, 0 и соответствующий ему высокочастотный сигнал с АМ (либо ЧМ, ФМ). Далее генерируется широкополосный шум со спектральной плотностью мощности, определяемой заданным ОСПШ, также отображаемым на экране. Изменение отношение осуществляется с шагом 1,0 клавишами "Pg Up", "Pg Down", a c шагом 0,1 клавишами "Up"(Ý) и "Down" (ß). Задание порога при АМ осуществляется клавишами "Left" (Ü) и "Right" (Þ).

Нажатием клавиши «Enter» инициируется изображение осциллограмм. Повторные нажатия дают другие реализации процессов, которые случайны из-за случайного характера шума.

Следует заметить, что выходные сигналы приёмников сдвинуты по отношению к предыдущим на один такт, равный длительности символа , так как решения о принятом символе принимается сравнением сигналов «0» и «1» (или с порогом при АМ) с выхода интеграторов в конце каждого символа.

1.2 Выбрать пункт «Амплитудная модуляция»

Зарисовать с экрана схему оптимального приемника.

1.2.1 Задать несколько значений ОСПШ на входе приемника, таких, чтобы ошибки приёма символов были не слишком редкими и их можно было наблюдать, порог - оптимальный. Занести в отчёт временные диаграммы сигналов на входе приёмника, выходах интеграторов и приёмника для двух ситуаций: ошибок нет, ошибка есть. У графиков проставить значение отношения сигнал/шум и порога.

1.2.2 Увеличить ОСПШ и соответственно значение оптимального порога и, наблюдая сигналы, отметить изменения по сравнению с предыдущей ситуацией и записать результаты наблюдения в отчёт.