Исследование помехоустойчивости оптимальных приёмников бинарных сигналов, страница 2

При выборе порога, отличного от оптимального, вероятность ошибки увеличивается (рисунок 3). Уменьшение порога приводит к увеличению составляющей ошибки  (т.е. передавался «0», а принято решение о наличии «1»), а увеличение порога – к увеличению  (т.е. передавалась «1», а принято решение о наличии «0»).

Частотная модуляция

В РС с частотной модуляцией (ЧМ) информационные сигналы имеют вид (рисунок 4)     

Рисунок 3 - Зависимость вероятности ошибки приема от значения порога при АМ

Рисунок 4 – Структура (а) и спектр (б) сигнала с ЧМ

Структура оптимального приемника ЧМ сигналов соответствует схеме, приведенной на рисунке 1.  На входах решающего устройства присутствуют величины  и  с распределениями, представленными на рисунке 2. Величина  присутствует на выходе неактивного в данный момент канала, а величина  - на выходе активного канала.

Следует отметить, что величины  и  являются некоррелированными, так как каждый канал обрабатывает смесь сигнала и шума в своей полосе частот, которая определяется опорным сигналом.

Для ЧМ сигналов  зависит от отношения разности частот сигналов «0» и «1» к тактовой частоте передатчика

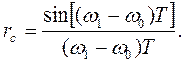
Оптимальным значением коэффициента является

При этом .

Однако на практике с целью упрощения схемы радиоприемного устройства принимают  Тогда .

Фазовая модуляция

Фазовая двоичная модуляция (манипуляция) является частным случаем бинарной (двоичной) модуляции с противофазными сигналами.

В РС с фазовой модуляцией (ФМ) информационные сигналы имеют вид

Структура оптимального приемника ФМ сигналов соответствует схеме, приведенной на рисунке 5. 

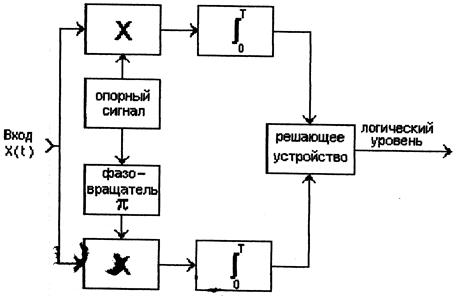
Рисунок 5 – Структурная схема приемника ФМ сигналов

Распределения случайных величин  и  показаны на рисунке 6. Как видно из рисунка, решающее устройство приемника сравнивает величины с разницей в их математических ожиданиях, в 2 раза большей, чем в случае ЧМ, и в 4 раза большей, чем при АМ. 

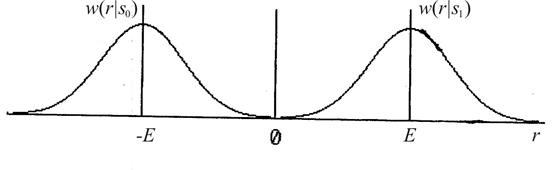
Рисунок 6 – Плотности вероятности сигналов на на выходе оптимального приемника в системах с ФМ

При ФМ величина  зависит от сдвига фаз между сигналами логических «0» и «1» и при их прямоугольной огибающей равна .

При   и .

На рисунке 7 представлены зависимости вероятности ошибки приема 1 бита от ОСПШ для АМ, ЧМ и ФМ.

Рисунок 7 – Зависимость  от ОСПШ для детерминированных сигналов (сплошные линии) и для сигналов со случайными начальными фазами (штриховые линии)

Таким образом, наибольшей потенциальной помехоустойчивостью обладают ФМ сигналы. Они обеспечивают выигрыш в энергии сигнала (при достижении одинаковой вероятности ошибки) в два раза по сравнению с ЧМ сигналами и в четыре раза по сравнению с АМ сигналами. ЧМ сигналы обеспечивают выигрыш в энергии сигнала по сравнению с АМ сигналами в два раза.

Однако следует иметь в виду, что, в отличие от ФМ и ЧМ, при амплитудной манипуляции передается только сигнал одного логического уровня. Поэтому если исходить из среднеэнергетических затрат, то нетрудно видеть, что системы с АМ и ЧМ сигналами обладают одинаковой помехоустойчивостью.

Оценка объема выборки символов , необходимого для экспериментальной оценки вероятности ошибки с приемлемой точностью

Определить требуемый объём выборки можно следующим образом. В результате эксперимента определяется частота ошибок, являющаяся оценкой вероятности , где число ошибок в выборке объёмом . Если  - истинное значение вероятности, то относительная погрешность оценки вероятности

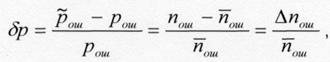
где   отклонение числа ошибок от среднего . Отклонение числа ошибок можно считать случайной величиной, распределённой нормально с дисперсией   . Максимальное значение  , следовательно,

Отсюда можно найти требуемый объём выборки  N , если задаться погрешностью оценки вероятности  и ожидаемым значением  :

.

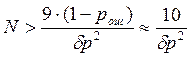В соответствии с этой формулой при = 0.1 и = 0,3    > 1000.