Исследование помехоустойчивости оптимальных приёмников бинарных сигналов

Лабораторная работа № 1

"Исследование помехоустойчивости

оптимальных приёмников бинарных сигналов"

ЦЕЛЬ РАБОТЫ

1. Изучение схем оптимальных приемников бинарных сигналов, преобразований сигналов в этих схемах как функции времени и частоты.

2. Уяснение механизма появления ошибок приёма символов и качественное сравнение потенциальной помехоустойчивости различных бинарных сигналов (амплитудная, частотная, фазовая манипуляция).

3. Определение зависимости вероятности ошибки приёма символа р от энергетического отношения сигнал/шум e/n₀ на входе приёмников для АМн, ЧМн, а также порога при АМн.

4. Сравнение потенциальной помехоустойчивости АМн, ФМн, ЧМн сигналов.

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Помехоустойчивость - это способность радиосистемы (РС) обеспечивать передачу сообщений с заданным качеством в условиях воздействия помех. Помехоустойчивость РС существенно зависит от отношения мощностей полезного сигнала, помех и шума (ОСПШ).

Количественно помехоустойчивость РС передачи дискретных сообщений характеризуется вероятностью ошибки при заданном ОСПШ на входе приемника системы или требуемым ОСПШ, обеспечивающим заданную вероятность ошибки .

Теоретически предельно достижимую помехоустойчивость РС называют потенциальной помехоустойчивостью. Реализовать потенциальную помехоустойчивость возможно только при использовании оптимальных методов приема. Одной из основных задач оптимального приема в цифровых РС является различение двух сигналов, каждый из которых соответствует одному из логических уровней. Для решения этой задачи используются двухканальные приемники, причем каждый из каналов строится на основе оптимального линейного (согласованного) фильтра или коррелятора. Корреляторы удобно использовать тогда, когда время наблюдения достаточно велико. Согласованные фильтры в основном используются при относительно малом времени наблюдения. В каждом канале такого приемника вычисляется апостериорная вероятность наличия того или иного сигнала или монотонная функция, однозначно с ней связанная. После чего решающее устройство путем сравнения апостериорных вероятностей принимает решение о формировании на своем выходе соответствующего логического уровня. Структурная схема оптимального приемника бинарных (двоично модулированных) сигналов представлена на рисунке 1.

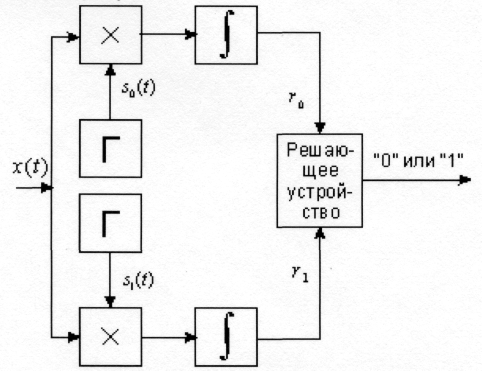
Рисунок 1 - Структурная схема оптимального приемника бинарных сигналов

В каждом канале такого приемника вычисляется корреляционный интеграл вида

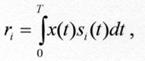                                                                                                                             (1)

где      i-й полезный сигнал (i = 0,1);

аддитивная смесь сигнала и помехи (шума) на входе приемника;

 интервал наблюдения.

Максимума корреляционный интеграл (1) достигает в момент времени , соответственно, принятие решения о наличии того или иного сигнала также должно производиться в этот момент времени.

При анализе помехоустойчивости оптимальных приемников делаются следующие допущения:

- помеха представляет собой «белый» шум (по крайней мере в пределах спектра сигнала);

- смесь сигнала и помехи является аддитивной;

- полезные сигналы, используемые в системе, известны с точностью до фазы.

Для полностью известных полезных сигналов

,                                                                                                                         (2)

где      интеграл вероятности;

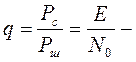 ОСПШ на входе приемника РС;

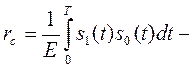 коэффициент взаимной корреляции сигналов логических «0» и «1»;

средние мощности полезного сигнала и помех (шумов);

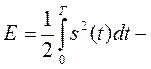  энергия полезного сигнала (в пересчете на 1 бит);

 спектральная плотность мощности шума.

Коэффициент , определяющий помехоустойчивость, существенно зависит от вида модуляции.

Амплитудная модуляция

В РС с амплитудной модуляцией (АМ) и пассивной паузой информационные сигналы имеют вид

В связи с тем, что один из сигналов равен 0, задача различения сигналов сводится к задаче обнаружения сигнала. При этом структура оптимального приемника также упрощается: один из каналов исключается, и вместо его выходного сигнала (1) на  решающее устройство подается постоянный пороговый уровень, определяющий вероятность обнаружения

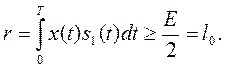
Плотности вероятности  и  описываются гауссовскими законами (рисунок 2) с параметрами:

- «0»: математическое ожидание , дисперсия ;

- «1»: математическое ожидание , дисперсия .

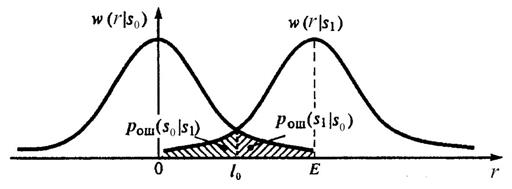
Рисунок 2 – Плотности вероятности сигналов на выходе оптимального приемника в системах с АМ и пассивной паузой

Если РС является симметричной, т.е. априорная вероятность передачи логических «0» и «1» одинакова, то средняя вероятность ошибки

.

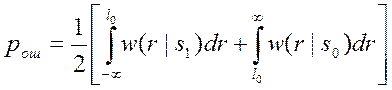Можно показать, что

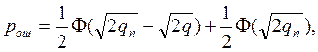
где     относительный порог обнаружения.

В этом случае необходимо также обеспечить и равную апостериорную вероятность ошибок приема «0» вместо «1» и «1» вместо «0». Отсюда следует, что оптимальный порог обнаружения должен быть равен ординате точки пересечения плотностей вероятности  и , т.е. .

При оптимальном выборе порога приемника АМ сигналов  и

.