Факторизация системы логических уравнений, полученной методом ПМФ
Первый цикл факторизации
Сформируем
выражение ![]() ,
включающее:
,
включающее:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Проведем поиск дизъюнктивных факторов и сформируем множество дизъюнктивных факторов:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Проведем оценку их качества:
|
Функция |
Фактор |
Порождающее множество |
Качество |
|
|
|
|
6 |
|
|
|
|
3 |
|
|
|
|
7 |
|
|
|
|
5 |
|
|
|
|
7 |
|
|
|
|
7 |
|
|
|
7 |
Наибольшим качеством обладают четыре фактора. Для факторизации могут быть использованы все четыре фактора, поскольку конъюнкции, входящие в их состав не встречаются в других факторах. В результате факторизации получаем следующую систему уравнений:
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]()
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]()
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
|
Номер импликанты |
Фактор |
Порождающее множество |
Качество |
|
1 |
|
1,5,7,8,10,11,14,17,18,22,23,24,29,30,33,34,36,37,38,40,41 |
13 |
|
|
1,6,8,9,12,17,18,20,21,24,27,30,33,34,35,37,38,41 |
10 |
|
|
2 |
|
2,6,7,9,12,17,19,20,21,25,26,31,33,34,35,36,39,40 |
10 |
|
|
2,5,7,8,10,13,16,19,20,22,23,25,29,31,33,35,36,37,39,40,41 |
13 |
|
|
7 |
|
3,7,8,13,14,15,19,21,22,27,28,32,34,36,38,39,41 |
8 |
|
|
4,7,8,11,15,16,18,21,22,26,28,32,35,37,38,39,40 |
8 |
|
|
|
7,33,34,36,40 |
9 |
|
|
|
7,8,14,22,28,34,36,38,41 |
12 |
|
|
|
5,7,8,10,22,23,28,29,33,36,37,40,41 |
23 |
|
|
|
7,8,11,18,22,28,37,38,40 |
13 |
|
|
|
7,19,21,34,36,39 |
9 |
|
|
|
2,7,19,20,25,31,33,35,36,39,40 |
17 |
|
|
|
7,21,26,35,39,40 |
11 |
|
|
|
7.8,13,19,22,28,36,39,41 |
13 |
|
|
|
7,8,15,21,22,28,32,38,39 |
15 |
|
|
|
7,8,16,22,28,35,37,39,40 |
13 |
|
|
|
7,34,36 |
4 |
|
|
|
7,33,36,40 |
10 |
|
|
|
7,40 |
4 |
|
|
|
7,8.22,28,36,41 |
15 |
|
|
|
7,8,22,28,38 |
13 |
|
|
|
7,8,22,28,37,40 |
15 |
|
|
|
7,19,36 |
8 |
|
|
|
7,21,39 |
6 |
|
|
|
7,35,39,40 |
8 |
|
|
|
7,8,22,28,39 |
13 |
|
|
|
7,36 |
3 |
|
|
|
7 |
0 |
|
|
|
7,40 |
3 |
|
|
|
7,8,22,28 |
10 |
|
|
|
7,39 |
3 |
|
|
8 |
|
1,8,17,18,24,30,33,34,37,38,41 |
11 |
|
|
8,21,27,34,38,41 |
5 |
|
|
|
8,20,33,35,37,41 |
5 |
|
|
|
8,18,21,35,37,38 |
5 |
|
|
|
8,34,38,41 |
6 |
|
|
|
8,33,37,41 |
6 |
|
|
|
8,18,37,38 |
6 |
|
|
|
8,41 |
2 |
|
|
|
8,21,38 |
4 |
|
|
|
8,35,37 |
4 |
|
|
|
8,41 |
3 |
|
|
|
8,38 |
3 |
|
|
|
8,37 |
3 |
|
|
|
8 |
0 |
|
|
17 |
|
6,9,12,17,20,21,33,34,35 |
10 |
|
21 |
|
21,34 |
2 |
|
|
21,35 |
2 |
|
|
33 |
|
33,34 |
2 |
|
|
33,35 |
2 |
Наибольшим
качеством обладает фактор ![]() .
Выбираем его и производим факторизацию.
.
Выбираем его и производим факторизацию.
Второй цикл факторизации
Сформируем
выражение ![]() ,
включающее:
,
включающее:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Дальнейший процесс факторизации приводит к следующему результату:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Суммарная
сложность уравнений ![]() операторов
И, ИЛИ, НЕ.
операторов
И, ИЛИ, НЕ.
Факторизация системы логических уравнений, полученной методом минимизации
Для логических уравнений, полученных в результате минимизации, дизъюнктивные факторы отсутствуют, в связи с чем факторизация возможна лишь путем формирования конъюнктивных факторов. В результате получаем следующие скобочные представления функций:
![]()
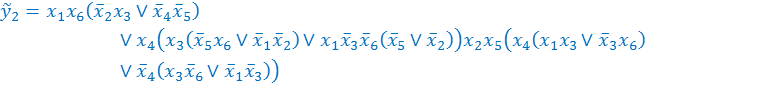
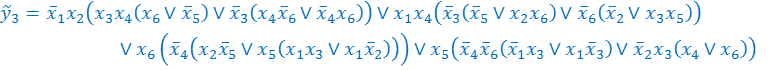
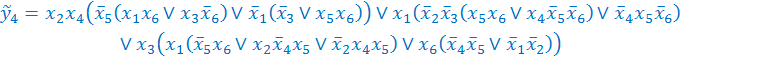
Суммарная
сложность уравнений ![]() операторов
И, ИЛИ, НЕ.
операторов
И, ИЛИ, НЕ.
|
Метод |
Сложность |
Максимальная глубина |
|
ПМФ |
80 |
12 |
|
Минимизация |
126 |
12 |
Лучший результат получен методом ПМФ.
Дальнейшие расчеты будут проводиться для представлений ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
полученных этим методом.
,
полученных этим методом.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.