Исследование КПД источника тока (Лабораторная работа № 2-5)

РАБОТА № 2-5 ИССЛЕДОВАНИЕ КПД ИСТОЧНИКА ТОКА

ЦЕЛЬ: экспериментально установить зависимость полезной мощности от тока в цепи и сопротивления нагрузки; проверить условие максимальной мощности, выделяемой на нагрузке.

ОБОРУДОВАНИЕ: амперметр, цифровой вольтметр, два реостата, источник тока.

ОСНОВЫ ТЕОРИИ

Электрическая цепь состоит из двух существенно различных частей: внешней, на которой выделяется полезная мощность и внутренней, содержащей источник тока (рис. 1).

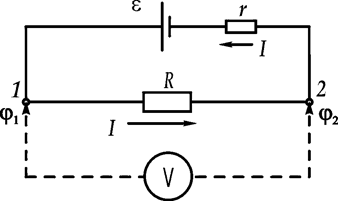
Рис. 1.

Источник тока характеризуется электродвижущей силой e и внутренним сопротивлением r. Электродвижущей силой источника тока называется его энергетическая характеристика, которая численно равна работе сторонних сил по перемещению положительного единичного заряда внутри источника.

Рассмотрим электрическую цепь с направлением обхода против часовой стрелки (рис. 1). Работа электростатических сил при перемещении заряда по замкнутому контуру равна нулю. Поэтому полная работа A₀ на внутреннем и внешнем участках будет равна работе сторонних сил. По определению э.д.с. эта работа равна

                                       (1)

Сторонние силы действуют внутри источника. Часть работы сторонних сил на внутреннем участке 2-e-1 идет на увеличение потенциальной энергии зарядов (создание и поддержание электростатического поля с разностью потенциалов j₁ - j₂ ), другая часть работы А_внт превращается в тепло внутри источника.

                             (2)

Полезная работа на внешнем участке 1-2 совершается за счет энергии электростатического поля

                        (3)

Эта работа идет на преодоление сопротивления движению заряда и превращается в тепло (в нагревательном элементе). Кроме того, эта энергия может быть преобразована в механическую работу (в электродвигателе) или химическую энергию (при зарядке аккумулятора). При этом на внешнем участке будут действовать также сторонние силы (э.д.с. электромагнитной индукции, возникающая при вращении ротора двигателя или э.д.с. аккумулятора). Ради простоты, однако, будем считать, что на внешнем участке сторонние силы отсутствуют (нагрузка представляет собой нагревательный элемент, обладающий сопротивлением R).Потери энергии внутри источника согласно формулам (1), (3) равны

             (4)

Правая часть равенства (4) имеет смысл полной работы сторонних и электростатических сил по перемещению заряда q на внутреннем участке в направлении тока.

Величина, равная

                             (5)

является падением напряжения на внутреннем участке 2-e-1 (с учетом направления обхода). В соответствии с законом Ома это падение напряжения равно

                                     (6)

Падение напряжения на внешнем участке 1-R-2 равно

                             (7)

Закон Ома для замкнутой цепи

                                   (8)

по существу выражает закон сохранения энергии в форме (2) при . Вольтметр, подключенный к клеммам нагрузки покажет разность потенциалов между этими точками, которая равна падению напряжения на внешнем участке (т.к. э.д.с. на этом участке отсутствует).

Тогда из формул (5) и (6) следует

                          (9)

Формула (9) выражает закон перераспределения напряжения между внутренним и внешним участками цепи: напряжение на внешнем участке будет меньше э.д.с. на величину падения напряжения внутри источника.

Зависимость U_н (I) в соответствии в формулой (9) является линейной: коэффициент пропорциональности равен внутреннему сопротивлению, а свободный член - э.д.с. При уменьшении сопротивления нагрузки и возрастании тока в цепи показания вольтметра будут уменьшаться. Если же цепь разомкнута, а сопротивление вольтметра велико, то ток в цепи будет весьма мал, и показания вольтметра будут близки к э.д.с.

Умножив правую и левую часть уравнения (9) на силу тока I, получим закон перераспределения мощности

                                                                                                     (10)

или

                                                                                                    (10’)

Здесь:

                                                                                                     (11)

- это полезная мощность, выделяемая на нагрузке.

Первый член в правой части

                                                                                                    (11’)

- это мощность, развиваемая источником (линейно зависит от тока).

Второй член в правой части

                                       (11”)

- мощность потерь внутри источника (квадратичная функция тока).

При I = 0, а также I = e/r - короткое замыкание: R = 0 - полезная мощность равна 0. При разомкнутой цепи (R =¥ , I = 0 ) источник не работает, а в режиме короткого замыкания вся мощность источника превращается в тепло внутри источника. Зависимость P_н (I) будет иметь максимум, это можно увидеть качественно при графическом анализе формулы (10).

Выясним, при каких условиях полезная мощность будет иметь максимальное значение. Исследуем функцию (10) на экстремум. При I = I_m