Исследование переходных процессов при разрядке конденсатора. Определение степени влияния параметров цепи на скорость разряда конденсатора на резистор

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Амурский Государственный Университет

(ГОУ ВПО «АмГУ»)

Кафедра: АПП и Э

Лабораторная работа по ТОЭ № 16

На тему: Исследование переходных процессов при разрядке конденсатора

Выполнил студент 542 г.                                                           Н.Г. Поткин

Преподаватель                                                                            Т.В. Карпова                                                                        

Благовещенск 2007

Лабораторная работа № 16

Исследование переходных процессов при зарядке конденсатора.

Цель работы: определить степень влияния параметров цепи на скорость разряда конденсатора на резистор; найти параметры цепи по осциллограммам переходного процесса.

Краткая теория

Конденсатор, предварительно заряженный до напряжения U₀ и подключенный к резистору с сопротивлением R, разряжается, причём напряжение на нём изменяется по закону u₀=U₀e^-t/τ, где τ=RС – постоянная  времени цепи, определяющая промежуток в е раз. График напряжения имеет вид, представленный на рисунке 1.

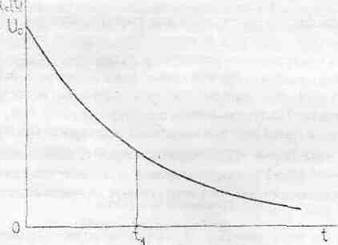
Рис 1.

Зная напряжение в моменты t=0 t=t₁, т.е. u_c(t₀)=U₀, и u_c(t₁)=U₀^-t/τ, можно определить постоянную времени цепи и ёмкость конденсатора при известном сопротивлении резистора R:

C = τ / R, τ = t₁ / ln U₀ / u_c(t₁)

Постоянную времени цепи можно найти графическим способом. Для этого нужно провести касательную к кривой напряжения в любой её точке. Постоянная времени выражается длиной подкасательной, выраженной в секундах (с).

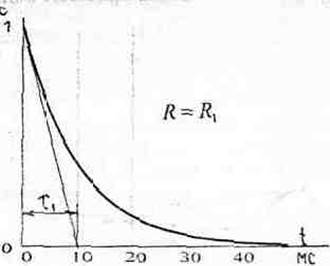
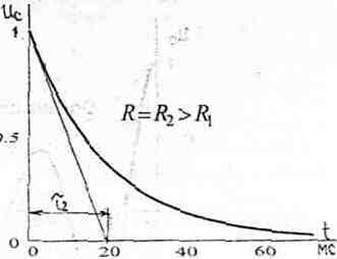
Рис 2.

Из графического способа определения τ следует, что увеличение R при

С = соnst замедляет разряд конденсатора. К такомуже эффекту приводит увеличение С при R = сonst.

При разряде конденсатора на индуктивную катушку напряжение на конденсаторе

U_c=-U₀ (ω₀ / ω^’)*e^-σt _* sin (ω’t-θ)

при условии  R < 2(L / C)^1/2 , т. е. разрядносит колебательный характер. В  этом выражении:

σ = R / 2L;    ω₀ = 1 /(LC)^1/2;        ω’ = (ω₀² – σ²)^1/2

Т.к ω₀²= σ²+ (ω’)², входящие в это выражение величины можно представить в виде сторон прямоугольного треугольника, гипотенуза которого остаётся неизменной при изменении R=L=const, C= const:

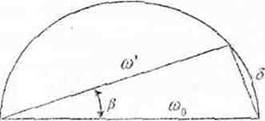
Рис 3.

Из рис. 3 видно, что увеличение сопротивления цепи приводит к уменьшению угловой частоты ω’ и к увеличению периода затухающих колебаний T =2π / ω’. Временная диаграмма напряжения на конденсаторе имеет вид:

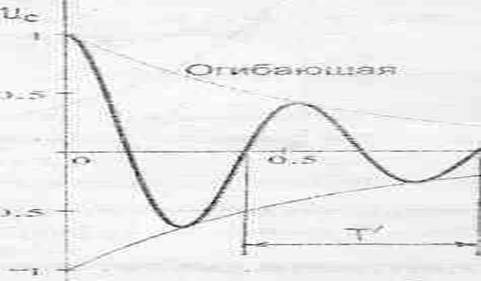
Рис. 4.

Быстроту затухания переходного процесса оценивают с помощью декремента колебания Δ, равного отношению двух соседних амплитуд одного знака:

Δ = u_c(t) / u_c(t+T’) = e^σT’

Используется и логарифмический декремент колебаний υ=ln Δ = σT’. Величины Δ и T’ можно определить по осциллограмме напряжения на емкости, что, в свою очередь, позволяет определить коэффициент затухания

σ =ln Δ/ Т', частоту незатухающих колебаний ω₀=(( ω’)²+σ²)^1/2  где ω’= 2π/T’, и индуктивность катушки L=1/ω₀²C при известном значении емкости конденсатора. Увеличением сопротивления резистора, включенного в RLC-цепь, можно перевести колебательный разряд в апериодический, который имеет место при условии R>2(L/C)^1/2=R_кр. Критическое сопротивление R_кр можно определить и по осциллограмме с учетом того, что при апериодическом разряде и его предельном случае напряжение не меняет своего знака.

Подготовка к работе

Конденсатор емкостью 1 мкФ, заряженный до напряжения 1В, подключается к резистору. Построить графики изменения напряжения на конденсаторе для двух значений сопротивления резистора: R=10 кОм и R=20 кОм. определить постоянные времени цепи графическим методом и сравнить их с τ=RС. Определить напряжение u_c при t₁=0,01 с по графику и по формуле  u₀=U₀e^-t/τ для случая R=10 кОм.    

        Выполнение работы

1. Подключить RС-цепь к генератору прямоугольных импульсов и снять с экрана осциллографа графики напряжения на емкости для двух значений сопротивления, заданных в п. 3, и емкости С = 1 мкф. Определить для каждого  случая τ и С графическим методом.

2. Исследовать влияние емкости на скорость разряда, для чего снять кривую при R = 10 кОм и С = 0.5 мкф.

3. Осуществить в RLС-цепи режим колебательного разряда конденсатора при С = 1 мкф. Снять кривую напряжения с экрана осциллографа, определить с ее помощью период Т' и частоту ω’ затухающих колебаний, декремент колебаний Δ ,коэффициент затухания σ  и параметры R и L индуктивной катушки.

4. Увеличивая сопротивление R. цепи, перевести колебательный разряд в апериодический, определив критическое сопротивление цепи. Снять с экрана осциллографа кривые апериодического разряда и его предельного случая.