



















подынтегральной функции в ряд; вычисление несобственных интегралов с применением весовых функций.
1. Квадратурные формулы с равноотстоящими узлами.
Заменяя подынтегральную функцию каким-либо интерполяционным многочленом, получаем квадратурные формулы вида
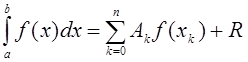 ,
(1)
,
(1)
где ![]() –
выбранные узлы интерполяции,
–
выбранные узлы интерполяции, ![]() – коэффициенты,
зависящие только от выбора узлов, но не от вида функции
– коэффициенты,
зависящие только от выбора узлов, но не от вида функции ![]() ,
R– остаточный член, или погрешность
квадратурной формулы. Отбрасывая остаточный член R, мы совершаем погрешность усечения. При расчете к ней
ещё добавляются различные погрешности округления.
,
R– остаточный член, или погрешность
квадратурной формулы. Отбрасывая остаточный член R, мы совершаем погрешность усечения. При расчете к ней
ещё добавляются различные погрешности округления.
Разобьем отрезок интегрирования [a,b] на ![]() равных частей системой точек
равных частей системой точек
![]() ,
, ![]() ,
, ![]() ,
, 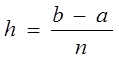 , и вычислим подынтегральную функцию в полученных узлах
, и вычислим подынтегральную функцию в полученных узлах
![]()
![]() .
.
Квадратурные формулы для равноотстоящих узлов называются формулами Ньютона – Котеса. Формулы Ньютона – Котеса различаются степенями использования интерполяционных многочленов. Чтобы не иметь дело с многочленами высоких степеней, обычно разбивают промежуток интегрирования на отдельные участки, применяют формулы Ньютона – Котеса с невысокими степенями на каждом участке и потом складывают полученные результаты (что даёт так называемые составные формулы).
а) формула трапеций:
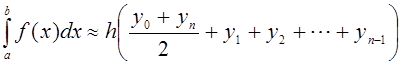 , (2)
, (2)
где ![]() .
.
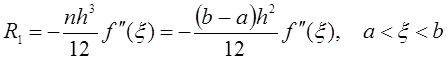 .
.
Формула трапеций даёт точное
значение, когда подынтегральная функция ![]() линейна,
ибо тогда
линейна,
ибо тогда ![]() .
.
б) формула Симпсона (формула парабол):
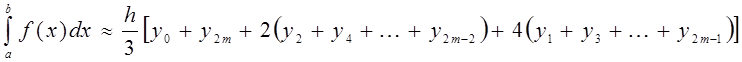 (3)
(3)
где 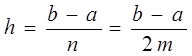
Остаточный член имеет вид
![]()
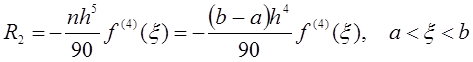 .
.
Формула Симпсона является точной для
многочленов до третьей степени включительно, т.к. в этом случае ![]() .
.
Заметим, что в формуле
Симпсона число узлов обязательно нечётное, т.е. ![]() четное,
четное, ![]() .
.
2. Квадратурные формулы Гаусса.
В квадратурных формулах Гаусса
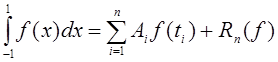 (4)
(4)
коэффициенты![]() и
абсциссы
и
абсциссы ![]()
![]() подбираются так, чтобы
формула была точной для всех многочленов наивысшей возможной степени
подбираются так, чтобы
формула была точной для всех многочленов наивысшей возможной степени ![]() . Числа
. Числа ![]() ,
, ![]() определены однозначно при
определены однозначно при ![]() . В табл. 1 приведены значения абсцисс
. В табл. 1 приведены значения абсцисс ![]() и коэффициентов
и коэффициентов ![]() ,
а также формулы остаточных членов
,
а также формулы остаточных членов ![]() при
при ![]() .
.
Таблица 1.
|
|
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
7 |
|
|
|
Неудобство применения
квадратурной формулы Гаусса состоит в том, что коэффициенты![]() и абсциссы
и абсциссы ![]() , вообще
говоря, иррациональные числа. Этот недостаток искупается ее высокой точностью
при сравнительно малом числе узлов интегрирования. В тех случаях, когда
подынтегральная функция сложна и на вычисление ее значений в каждом узле
интегрирования требуется много времени, применение формулы Гаусса особенно
выгодно.
, вообще
говоря, иррациональные числа. Этот недостаток искупается ее высокой точностью
при сравнительно малом числе узлов интегрирования. В тех случаях, когда
подынтегральная функция сложна и на вычисление ее значений в каждом узле
интегрирования требуется много времени, применение формулы Гаусса особенно
выгодно.
Получить оценку погрешности результата, используя формулу остаточного члена, для формул Гаусса удается очень редко, так как это связано с вычислением производных высоких порядков от подынтегральной функции (см. табл. 1).
При вычислении интеграла 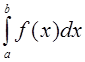 следует сделать замену переменной
следует сделать замену переменной 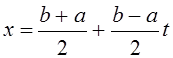 . Тогда формула Гаусса будет иметь вид:
. Тогда формула Гаусса будет иметь вид:
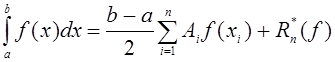 ,
(5) где
,
(5) где 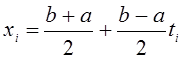 (6)
(6)
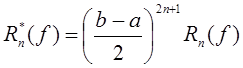 (7)
(7)
Пример 1. По формуле Гаусса при n=5 вычислить интеграл
I = 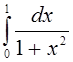
Решение. Сделаем замену
переменной 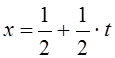 .
.
Получим интеграл 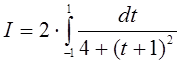 .
.
Составляем таблицу значений подынтегральной функции
|
|
|
|
|
|
1 |
- 0,906179846 |
0,24945107 |
0,236926885 |
|
2 |
- 0,538469310 |
0,23735995 |
0,478628670 |
|
3 |
0 |
0,2 |
0,568888889 |
|
4 |
0,538469310 |
0,15706261 |
0,478628670 |
|
5 |
0,906179846 |
0,13100114 |
0,236926885 |
и затем по формуле Гаусса при n=5 находим
![]() .
.
3. Интегрирование с помощью степенных рядов.
Рассмотрим определенный интеграл
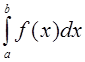 .
(8)
.
(8)
Пусть подынтегральная функция ![]() разлагается в степенной ряд
разлагается в степенной ряд 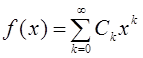 , сходящийся в интервале
, сходящийся в интервале ![]() , который содержит отрезок интегрирования
, который содержит отрезок интегрирования ![]() .
.
По теореме о почленном интегрировании степенных рядов можно представить интеграл (1) в виде числового ряда
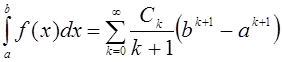 . (9)
. (9)
Если ряд (9) сходится достаточно быстро, то можно приближенно вычислить определенный интеграл с помощью частичной суммы ряда
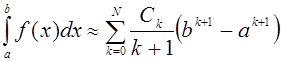 .
(10)
.
(10)
Для знакочередующегося ряда, с монотонно убывающими по абсолютной величине членами, абсолютная величина остатка ряда не превосходит абсолютной величины первого из отбрасываемых членов ряда. Для оценки остатка ряда в других случаях применяют замену такими числовыми рядами, остатки которых легко оцениваются.
Пример 2. Вычислить интеграл 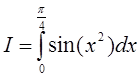 с точностью до
с точностью до ![]() путем
разложения подынтегральной функции в степенной ряд.
путем
разложения подынтегральной функции в степенной ряд.
Решение. Разложим функцию
![]() в степенной ряд
в степенной ряд
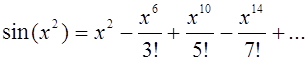
Этот ряд сходится при любом х.
Проинтегрируем его почленно в пределах от ![]() до
до ![]() :
:
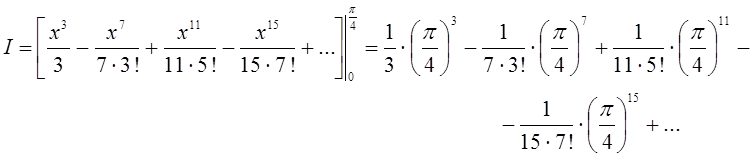
Так как полученный числовой ряд является знакочередующимся, то достаточно выбрать такое число членов, чтобы первый из отброшенных
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.