План-конспект урока по информатике, проводимого в 9 классе на тему: "Вычисление площади фигуры, границы которой заданы графиками функции"

План-конспект урока информатики, проводимого в 9 ”М” классе.

Тема урока: “Вычисление площади фигуры, границы которой заданы графиками функции”.

Дата: 26.04.2005 г.

Цели урока:

Образовательные: закрепить с учащимися метод Монте-Карло на примере задачи вычисления площади фигуры, границы которой заданы графиками функции.

Развивающие: формирование логического и аналитического мышления, развитие познавательного интереса к предмету, развитие умения планировать свою деятельность.

Воспитательные: обеспечить интерес учащихся путем акцентирования практической значимости использования данной темы. Стимулировать ответственное отношение учащихся к учебной работе путем поощрения их участия в работе на уроке.

План урока:

1.  Организационный момент (1-2 мин).

2.  Проверка домашнего задания (8-10 мин).

3.  Изложение нового материала (10-15 мин.)

4.  Закрепление нового материала (10-13 мин).

5.  Подведение итогов урока (2-3 мин.)

6.  Домашнее задание (1-2 мин.)

Ход урока:

1.  Организационный момент:

- приветствие;

- проверка готовности к уроку;

- проверка отсутствующих;

- объявление темы и целей урока;

2.  Проверка домашнего задания:

1)  С каким методом вы познакомились на прошлом уроке? (С методом Монте-Карло)

2)  Почему этот метод получил такое название? (По названию секретного проекта, который проводился перед Второй мировой войной в интересах армии США и в котором он впервые использовался. Название метода связано со случайностями игрового бизнеса, одним из центров которого является курорт Моте-Карло)

3)  Какое другое название имеет метод Монте-Карло? (Метод статистических испытаний)

4)  На каком примере вы рассматривали суть метода Монте-Карло? (На примере задачи определения площади плоской фигуры)

5)  Что такое датчик случайных чисел? (При обращении в алгоритме к датчику компьютер выдает одно случайное число, при новом обращении – новое случайное число)

3.  Изложение нового материала:

Итак, на дом вам надо было самостоятельно разобрать §97, т.е. ознакомиться с материалом сегодняшнего урока. Поэтому  изложение нового материала я буду с вашей помощью и в то же время проверю то, как вы подготовились к сегодняшнему уроку.

ПОСТАНОВКА ЗАДАЧИ:

Методом Монте-Карло найдите площадь фигуры, ограниченной линиям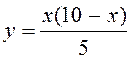и

 и .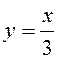

ОЦЕНКА ИМЕЮЩЕЙСЯ ИНФОРМАЦИИ И ВЫБОР ПЛАНА СОЗДАНИЯ МОДЕЛИ:

Все конкретные ограничения и условия в задаче известны. Задан также и метод решения задачи.

Сначала нужно построить графики функций и определиться с фигурой известной площади, а затем, используя алгоритм МонтеКарло1, построить компьютерную реализацию модели.

Таким образом, имеем план:

За — создание документальной математической реализации модели;

3б—создание    компьютерной    реализации    модели.

СОЗДАНИЕ ДОКУМЕНТАЛЬНОЙ МАТЕМАТИЧЕСКОЙ РЕАЛИЗАЦИИ МОДЕЛИ:

Строим графики функций и определяем фигуру 1, площадь которой нужно вычислить. Затем строим прямоугольник (фигура 2), который содержит в себе фигуру 1 и площадь которого S₀ вычислить легко (рис. 1).

Вычислять точки пересечения линий фигуры 1 (параболы и прямой) не обязательно. Главное, чтобы эти точки оказались внутри фигуры 2. В частности, для задачи в качестве фигуры 2 можно брать прямоугольник 10*5.

Отсюда следует, что координата xслучайной точки принадлежит отрезку , а координата y – отрезку .

Формула для вычислений искомой площади S будет иметь вид:

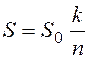, где n– общее число случайных точек, попавших на фигуру 2,

k – число случайных точек, попавших на фигуру 1.

Так как площадь S₀ фигуры 2 (прямоугольника) равна 50, то формула для вычисления площади фигуры 1 примет вид:

.

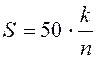4.  Закрепление нового материала

Итак, если вы поняли  данную задачу, то самостоятельно по вариантам делаем следующие задачи:

1 вариант: методом Монте-Карло найдите площади фигур, ограниченных линиям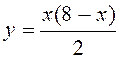и  и 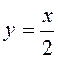 (стр. 519 б).

2 вариант: методом Монте-Карло найдите площади фигур, ограниченных линиям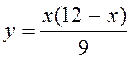и  и 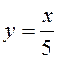 (стр. 519 д).

5.  Подведение итогов урока

Итак, сегодня мы с вами разобрали, как методом Монте-Карло вычислять площадь фигуры, границы которой заданы графиками функции.

Выставляю оценки за работу на уроке.

6.  Задание домашнего задания

Для тех, кто не справился с заданием на уроке, задача остается на дом.

§96-97.